TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 6.2 Goniometrische verhoudingen VWO 3
Boek: Getal & Ruimte - Goniometrie VWO 3 (deel 2) opgaven 10 t/m 27, 2011We hebben de volgende goniometrische verhoudingen: SIN, COS, TAN.
Let wel: dit betreft een verhouding. Dus een breuk. Dus de 'sinus van een hoek' is een breuk.
Wil je de hoek in graden weten, gebruik dan de inverse sinus: sin-1. De goniometrische verhoudingen zijn (SOS CAS TOA):
sin(∠A) (SOS) = overstaande rechthoekszijde van die ∠A / schuine zijde
cos(∠A) (CAS) = aanliggende rechthoekszijde van die ∠A / schuine zijde
tan(∠A) (TOA) = overstaande rechthoekszijde van die ∠A / aanliggende rechthoekszijde van die ∠A
Let wel: dit betreft een verhouding. Dus een breuk. Dus de 'sinus van een hoek' is een breuk.
Wil je de hoek in graden weten, gebruik dan de inverse sinus: sin-1. De goniometrische verhoudingen zijn (SOS CAS TOA):
sin(∠A) (SOS) = overstaande rechthoekszijde van die ∠A / schuine zijde
cos(∠A) (CAS) = aanliggende rechthoekszijde van die ∠A / schuine zijde
tan(∠A) (TOA) = overstaande rechthoekszijde van die ∠A / aanliggende rechthoekszijde van die ∠A
10.
b. Je hebt de verhouding AB/AC, want die is 4/5 = 0,8
11.
b. sin(∠C) = AB / AC
c. tan(∠A) = BC / AB
d. cos(∠C) = BC / AC
12.
b. cos(∠B) = BD / AB
c. tan(∠A1) = BD / AD
d. sin(∠A2) = CD / AC
e. cos(∠C) = CD / AC
f. tan(∠B) = AD / BD
13.
a. tan(∠A) = CD / AD
b. sin(∠B) = CD / BC
c. cos(∠C1) = CD / AC
d. sin(∠C2) = BD / BC
14.
b. sin(∠A) = 0,81 dat geeft ∠A = sin-1(0,81) ≈ 54,1º
c. tan(∠A) = 0,81 dat geeft ∠A = tan-1(0,81) ≈ 39,0º
d. cos(∠A) = 0,08 dat geeft ∠A = cos-1(0,08) ≈ 85,4º
e. sin(∠A) = 0,02 dat geeft ∠A = sin-1(0,02) ≈ 1,1º
f. cos(∠A) = 0,98 dat geeft ∠A = cos-1(0,98) ≈ 11,5º
15.
b. cos(∠B) = BC/AB = 7/9, dus ∠B ≈ 38,9º
16.
cos(∠A) = aanliggende rechthoekszijde / schuine zijde = A/S = AB/AC = 4/5
∠A = cos-1(4/5)
∠A ≈ 36,87º
b.
tan(∠F1) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = DG/FG = 2/5
∠F1 = tan-1(2/5)
∠F1 ≈ 21,80º
cos(∠F2) = aanliggende rechthoekszijde / schuine zijde = A/S = FG/EF = 5/9
∠F2 = cos-1(5/9)
∠F2 ≈ 56,25º
c.
tan(∠L1) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = KM/KL = 6/3
∠L1 = tan-1(6/3)
∠L1 ≈ 63,43º
sin(∠N) = overstaande rechthoekszijde / schuine zijde = O/S = KL/LN = 3/4
∠N = sin-1(3/4)
∠N ≈ 48,59º
17.
sin(∠B)
b.
sin(∠B) = O/S = AC/BC
sin(29º) = AC/7
AC = sin(29º) * 7
AC ≈ 3,39
18.
a. EF ≈ 3,48
b. DF met Stelling van Pythagoras DF ≈ √5,5296 ≈ 2,35
DF = 4,2 x cos(56º) ≈ 2,35
c. Cos is sneller en heeft dus de voorkeur.
19.
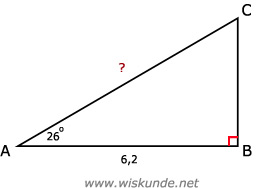
cos(26º) = 6,2/AC
AC = 6,2 / cos(26º)
AC ≈ 6,90
Tip:
Voor de sin(∠A) gebruik dan: SOS
a. Sin(∠A) = 3/5, dus ∠A = sin-1(3/5) ≈ 36,9º Voor de sin(∠A) gebruik dan: SOS
b. Je hebt de verhouding AB/AC, want die is 4/5 = 0,8
11.
Tip:
Leer de afkortingen van SOS CAS TOA uit je hoofd!
a. cos(∠A) = AB / AC Leer de afkortingen van SOS CAS TOA uit je hoofd!
b. sin(∠C) = AB / AC
c. tan(∠A) = BC / AB
d. cos(∠C) = BC / AC
12.
Tip:
Zie de rode winkelhaak (90º). Hierdoor weet je zeker dat het een rechthoekige driehoek is.
a. sin(∠C) = AD / AC Zie de rode winkelhaak (90º). Hierdoor weet je zeker dat het een rechthoekige driehoek is.
b. cos(∠B) = BD / AB
c. tan(∠A1) = BD / AD
d. sin(∠A2) = CD / AC
e. cos(∠C) = CD / AC
f. tan(∠B) = AD / BD
13.
a. tan(∠A) = CD / AD
b. sin(∠B) = CD / BC
c. cos(∠C1) = CD / AC
d. sin(∠C2) = BD / BC
14.
Tip:
Om de hoek te berekenen in graden, gebruik je de inverse: sin-1, cos-1, tan-1
a. cos(∠A) = 0,81 dat geeft ∠A = cos-1(0,81) ≈ 35,9º Om de hoek te berekenen in graden, gebruik je de inverse: sin-1, cos-1, tan-1
b. sin(∠A) = 0,81 dat geeft ∠A = sin-1(0,81) ≈ 54,1º
c. tan(∠A) = 0,81 dat geeft ∠A = tan-1(0,81) ≈ 39,0º
d. cos(∠A) = 0,08 dat geeft ∠A = cos-1(0,08) ≈ 85,4º
e. sin(∠A) = 0,02 dat geeft ∠A = sin-1(0,02) ≈ 1,1º
f. cos(∠A) = 0,98 dat geeft ∠A = cos-1(0,98) ≈ 11,5º
15.
Tip:
Draai je boek zo dat de rode winkelhaak (90º) op de "grond" ligt. Dan zie je het beter.
a. BC is de aanliggende rechthoekszijde en AB is de schuine zijdeDraai je boek zo dat de rode winkelhaak (90º) op de "grond" ligt. Dan zie je het beter.
b. cos(∠B) = BC/AB = 7/9, dus ∠B ≈ 38,9º
16.
Tip:
Bekijk eerst of je sin, cos of tan gaat gebruiken.
a.Bekijk eerst of je sin, cos of tan gaat gebruiken.
cos(∠A) = aanliggende rechthoekszijde / schuine zijde = A/S = AB/AC = 4/5
∠A = cos-1(4/5)
∠A ≈ 36,87º
b.
tan(∠F1) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = DG/FG = 2/5
∠F1 = tan-1(2/5)
∠F1 ≈ 21,80º
cos(∠F2) = aanliggende rechthoekszijde / schuine zijde = A/S = FG/EF = 5/9
∠F2 = cos-1(5/9)
∠F2 ≈ 56,25º
c.
tan(∠L1) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = KM/KL = 6/3
∠L1 = tan-1(6/3)
∠L1 ≈ 63,43º
sin(∠N) = overstaande rechthoekszijde / schuine zijde = O/S = KL/LN = 3/4
∠N = sin-1(3/4)
∠N ≈ 48,59º
17.
Tip:
Van belang zijn dus de overstaande (O) en de schuine (S). Dus de sin.
a.Van belang zijn dus de overstaande (O) en de schuine (S). Dus de sin.
sin(∠B)
b.
sin(∠B) = O/S = AC/BC
sin(29º) = AC/7
AC = sin(29º) * 7
AC ≈ 3,39
18.
a. EF ≈ 3,48
b. DF met Stelling van Pythagoras DF ≈ √5,5296 ≈ 2,35
DF = 4,2 x cos(56º) ≈ 2,35
c. Cos is sneller en heeft dus de voorkeur.
19.
Tip:
Je gebruikt de aanliggende rechthoekszijde (A) en de schuine zijde (S) van ∠A. Gebruik dus de cos.
cos(∠A) = A/S = AB/ACJe gebruikt de aanliggende rechthoekszijde (A) en de schuine zijde (S) van ∠A. Gebruik dus de cos.
cos(26º) = 6,2/AC
AC = 6,2 / cos(26º)
AC ≈ 6,90

20.
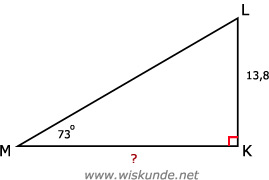
tan(73º) = 13,8/KM
KM = 13,8 / tan(73º)
KM ≈ 4,22
21.
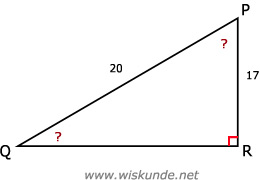
cos(∠P) = 17/20
∠P = cos-1(17/20)
∠P ≈ 31,8º
∠Q = 180º - 90º - 31,8º = 58,2º
22.
b. Met afronden wat het onnauwkeuriger.
c. ∠A = 70,5º
∠B = 70,5º
23.
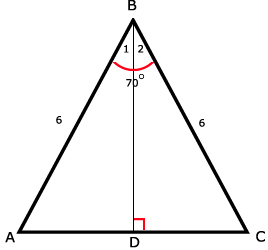
sin(∠B1) = AD / AB
AD = 6 x sin(35º) ≈ 3,441458
Hieruit volgt dat AC = 2 x AD ≈ 6,88
24.
tan(∠B) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = AC/AB
tan(28º) = 5/AB
AB = 5 / tan(28º)
AB ≈ 9,40
2) Bereken AD =>
∠C = 180º - 90º - 28º = 62º
sin(∠C) = overstaande rechthoekszijde / schuine zijde = O/S = AD/AC
sin(62º) = AD/5
AD = sin(62º) * 5
AD ≈ 4,41
3) Bereken CD =>
∠A1 = ∠CAD = 180º - 90º - 62º = 28º
sin(∠CAD) = overstaande rechthoekszijde / schuine zijde = O/S = CD/AC
sin(28º) = CD/5
CD = sin(28º) * 5
CD ≈ 2,35
25.
tan(42º) = 5/BC
BC = 5 / tan(42º)
BC ≈ 5,55
(AC = AB + BC)
tan(∠A) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = CD/AC = 5/13,55
∠A = tan-1(5/13,55)
∠A ≈ 20,3º
26.
tan(∠B) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = AD/AB
tan(30º) = AD/8
AD = tan(30º) * 8
AD ≈ 4,6
2)
tan(∠A1) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = BC/AB
tan(40º) = BC/8
BC = tan(40º) * 8
BC ≈ 6,7
3) EC = 6,7 - 4,6 = 2,1
4)
DE2 + CE2 = CD2
82 + (2,1)2 = CD2
CD2 = 68,41
CD = √68,41
CD ≈ 8,3
27.
cos(∠A) = aanliggende rechthoekszijde / schuine zijde = A/S = AE/AD
cos(60º) = AE/3,8
AE = cos(60º) * 3,8
AE = 1,9
b.
BF = 6,9 - 1,9 - 1,2 = 3,8
DE2 + AE2 = AD2
DE2 + (1,9)2 = 3,82
DE2 = 10,83
DE = √10,83
DE ≈ 3,29
tan(∠B) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = CF/BF = 3,29/3,8
∠B = tan-1(3,29/3,8)
∠B ≈ 40,9º
Tip:
Je gebruikt de overstaande rechthoekszijde (O) en de aanliggende rechthoekszijde (A) van ∠M. Gebruik dus de tan.
tan(∠M) = O/A = KL/KMJe gebruikt de overstaande rechthoekszijde (O) en de aanliggende rechthoekszijde (A) van ∠M. Gebruik dus de tan.
tan(73º) = 13,8/KM
KM = 13,8 / tan(73º)
KM ≈ 4,22

21.
Tip:
Het kan zijn dat jouw schets er iets anders uitziet dan mijn schets. Zolang je alles maar goed neerzet in de driehoek.
Bereken eerst ∠P en bereken daarna ∠Q met de hoekensom (180º).
cos(∠P) = aanliggende rechthoekszijde / schuine zijde = A/S = PR/PQHet kan zijn dat jouw schets er iets anders uitziet dan mijn schets. Zolang je alles maar goed neerzet in de driehoek.
Bereken eerst ∠P en bereken daarna ∠Q met de hoekensom (180º).
cos(∠P) = 17/20
∠P = cos-1(17/20)
∠P ≈ 31,8º
∠Q = 180º - 90º - 31,8º = 58,2º

22.
Tip:
Bij een gelijkbenige driehoek zijn de basishoeken ∠A en ∠B gelijk.
a. sin(∠C1) = AD/AC = 2/6, dus ∠C1 = sin-1(2/6) ≈ 19,5ºBij een gelijkbenige driehoek zijn de basishoeken ∠A en ∠B gelijk.
b. Met afronden wat het onnauwkeuriger.
c. ∠A = 70,5º
∠B = 70,5º
23.
Tip:
Bereken eerst AD met de sinus. Dan AC = 2 x AD.
∠B1 = ∠B2 = 70º/2 = 35ºBereken eerst AD met de sinus. Dan AC = 2 x AD.
sin(∠B1) = AD / AB
AD = 6 x sin(35º) ≈ 3,441458
Hieruit volgt dat AC = 2 x AD ≈ 6,88

24.
Tip:
Als je AD weet, dan kan CD eventueel ook met de Stelling van Pythagoras.
1) Bereken AB =>Als je AD weet, dan kan CD eventueel ook met de Stelling van Pythagoras.
tan(∠B) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = AC/AB
tan(28º) = 5/AB
AB = 5 / tan(28º)
AB ≈ 9,40
2) Bereken AD =>
∠C = 180º - 90º - 28º = 62º
sin(∠C) = overstaande rechthoekszijde / schuine zijde = O/S = AD/AC
sin(62º) = AD/5
AD = sin(62º) * 5
AD ≈ 4,41
3) Bereken CD =>
∠A1 = ∠CAD = 180º - 90º - 62º = 28º
sin(∠CAD) = overstaande rechthoekszijde / schuine zijde = O/S = CD/AC
sin(28º) = CD/5
CD = sin(28º) * 5
CD ≈ 2,35
25.
Tip:
Bereken eerst BC en gebruik dan de tan∠A.
tan(∠B) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = CD/BCBereken eerst BC en gebruik dan de tan∠A.
tan(42º) = 5/BC
BC = 5 / tan(42º)
BC ≈ 5,55
(AC = AB + BC)
tan(∠A) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = CD/AC = 5/13,55
∠A = tan-1(5/13,55)
∠A ≈ 20,3º
26.
Tip:
Teken de loodlijn DE loodrecht op BC als hulplijn. Punt E is het snijpunt van deze loodlijn met BC.
1) Bereken eerst AD met de tangens
2) Bereken dan BC met de tangens
3) EC = BC - BE (BE = AD)
4) Bereken dan CD met de Stelling van Pythagoras
1)Teken de loodlijn DE loodrecht op BC als hulplijn. Punt E is het snijpunt van deze loodlijn met BC.
1) Bereken eerst AD met de tangens
2) Bereken dan BC met de tangens
3) EC = BC - BE (BE = AD)
4) Bereken dan CD met de Stelling van Pythagoras
tan(∠B) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = AD/AB
tan(30º) = AD/8
AD = tan(30º) * 8
AD ≈ 4,6
2)
tan(∠A1) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = BC/AB
tan(40º) = BC/8
BC = tan(40º) * 8
BC ≈ 6,7
3) EC = 6,7 - 4,6 = 2,1
4)
DE2 + CE2 = CD2
82 + (2,1)2 = CD2
CD2 = 68,41
CD = √68,41
CD ≈ 8,3
27.
Tip:
Bereken eerst AE en bereken dan DE met de Stelling van Pythagoras.
Dan weet je ook CF.
BF = AB - AE - EF
Gebruik als laatste de tan(∠B)
a.Bereken eerst AE en bereken dan DE met de Stelling van Pythagoras.
Dan weet je ook CF.
BF = AB - AE - EF
Gebruik als laatste de tan(∠B)
cos(∠A) = aanliggende rechthoekszijde / schuine zijde = A/S = AE/AD
cos(60º) = AE/3,8
AE = cos(60º) * 3,8
AE = 1,9
b.
BF = 6,9 - 1,9 - 1,2 = 3,8
DE2 + AE2 = AD2
DE2 + (1,9)2 = 3,82
DE2 = 10,83
DE = √10,83
DE ≈ 3,29
tan(∠B) = overstaande rechthoekszijde / aanliggende rechthoekszijde = O/A = CF/BF = 3,29/3,8
∠B = tan-1(3,29/3,8)
∠B ≈ 40,9º
Andere paragrafen:
6.1. Hellingen (1 t/m 9)
6.2. Goniometrische verhoudingen (10 t/m 27)
6.3. Berekeningen met sinus, cosinus & tangens (28 t/m 38)
6.4. Berekeningen in de ruimte (39 t/m 49)
6.5. Lijnstukken berekenen (50 t/m 62)
6.1. Hellingen (1 t/m 9)
6.2. Goniometrische verhoudingen (10 t/m 27)
6.3. Berekeningen met sinus, cosinus & tangens (28 t/m 38)
6.4. Berekeningen in de ruimte (39 t/m 49)
6.5. Lijnstukken berekenen (50 t/m 62)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


