TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 2.2 De bissectrice VWO 2
Boek: Getal & Ruimte - Vlakke figuren VWO 2 (deel 1) opgaven 17 t/m 28, 2009Wat is een bissectrice?
Een bissectrice deelt een hoek in 2 gelijke stukken (hoeken). We noemen de bissectrice ook wel een deellijn.
Voor elk punt op de bissectrice geldt dat de afstand van dat punt tot beide benen gelijk is.
Stel dat een hoek A gelijk is aan 72 graden. De bissectrice deelt deze hoek dan in 2 gelijke hoeken van 36 graden.
Dus de bissectrice deelt een ∠A = 72º in 2 gelijke hoeken van: ∠A1 = 36º en ∠A2 = 36º.
Een bissectrice deelt een hoek in 2 gelijke stukken (hoeken). We noemen de bissectrice ook wel een deellijn.
Voor elk punt op de bissectrice geldt dat de afstand van dat punt tot beide benen gelijk is.
Stel dat een hoek A gelijk is aan 72 graden. De bissectrice deelt deze hoek dan in 2 gelijke hoeken van 36 graden.
Dus de bissectrice deelt een ∠A = 72º in 2 gelijke hoeken van: ∠A1 = 36º en ∠A2 = 36º.
17.
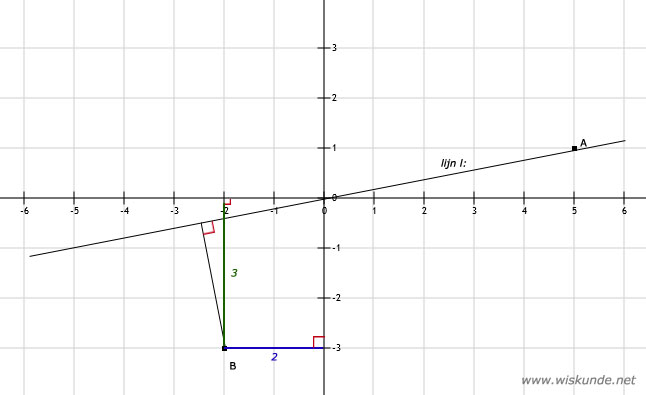
b. Teken een lijn door B loodrecht op l:. De afstand is ongeveer 2,5 cm.
c. De afstand van B tot de x-as is 3 cm en de afstand van B tot de y-as is 2 cm.
18.
b. Ja, dat klopt ook in de tekening.
19.
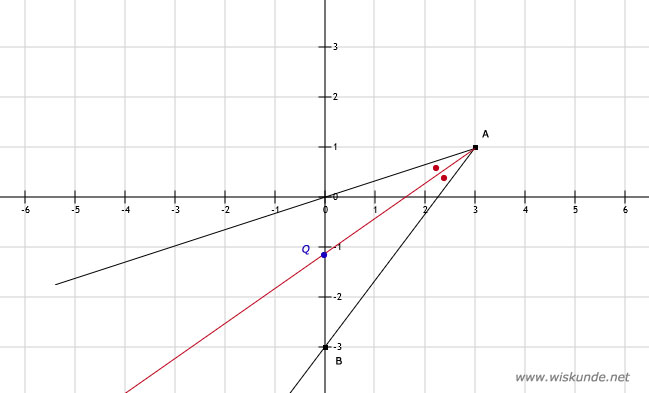
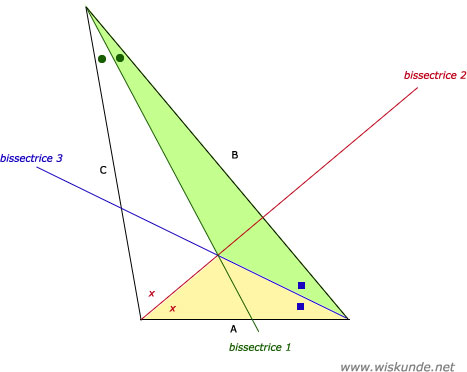
b. Rood is de bissectrice van hoek A.
c. Het blauwe punt Q is het snijpunt van de rode bissectrice en de y-as.
20.
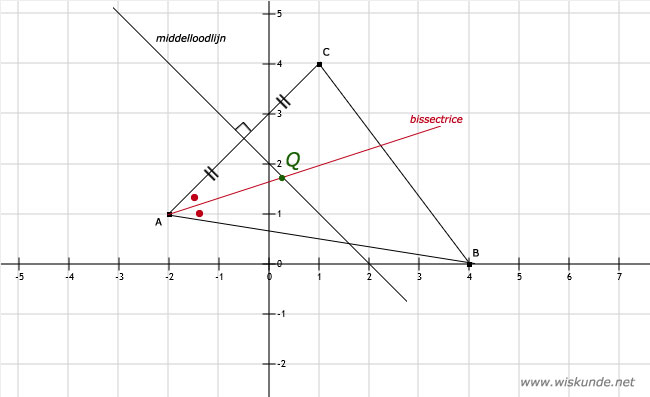
b. Teken de bissectrice van hoek A. Deze is rood in de afbeelding.
c. Teken de middelloodlijn van AC. Punt Q is snijpunt van de bissectrice en de middelloodlijn.
21.
22.
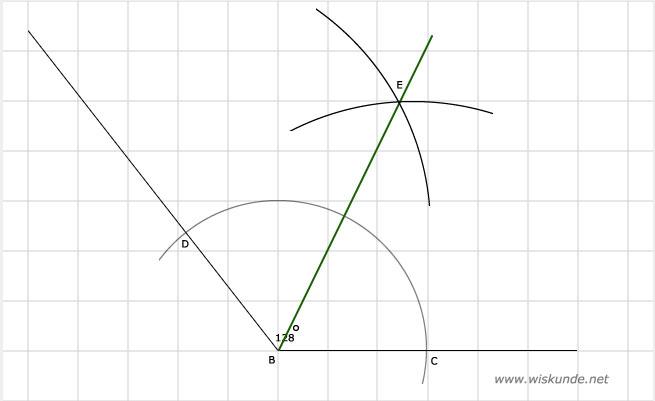
a. Hoe construeer je de bissectrice van een hoek B? Teken eerst een hoek B. Teken dan een cirkel met middelpunt B. Kies zelf een straallengte van de cirkel. Deze cirkel snijdt de benen van de hoek B in de punten C en D.
Teken nu een cirkel met middelpunt C en straal CD. En teken tevens een cirkel met middelpunt D en straal CD. Deze 2 cirkels snijden elkaar in 2 punten. Noem deze punten E en F.
Teken nu de lijn door hoekpunt B, E en F. Deze lijn is de bissectrice van hoek B.
b. Zie afbeelding
23.
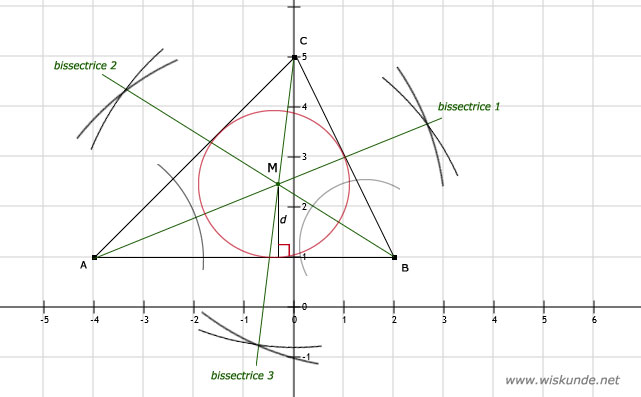
b. Zie afbeelding. Let wel: construeer is met je passer. Je mag dus niet opmeten!
c. Omdat M het middelpunt is van de ingeschreven cirkel. En de straal die loodrecht op de zijde staat, is de afstand van M tot die zijde. Deze 3 afstanden zijn steeds gelijk (gelijk aan r).
d. *
e. De afstand (d) van middelpunt tot zijde AB is ongeveer 1,5 cm.
f. Zie de rode cirkel
24.
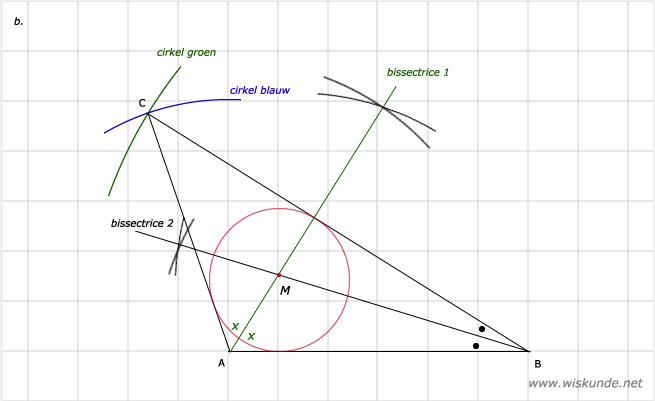
b. Zie afbeelding
c. volgt *
25.
b. ∠D1 = 180º - 48º - 31º = 101º
c. ∠E2 = 180º - 24º - 70º = 86º
26.
∠R = 180º - 44º - 38º = 98º
∠R1 = 1/2 x 98º = 49º
∠P1 + ∠M1 + ∠R1 = 180º
∠M1 = 180º - 22º - 49º
∠M1 = 109º
Bereken ∠S2:
∠P2 + ∠Q + ∠S2 = 180º
∠S2 = 180º - 22º - 38º
∠S2 = 120º
Tip:
Om de afstand van B tot lijn l: te bepalen, tekenen we de loodlijn door B loodrecht op l:.
a. Zie afbeeldingOm de afstand van B tot lijn l: te bepalen, tekenen we de loodlijn door B loodrecht op l:.
b. Teken een lijn door B loodrecht op l:. De afstand is ongeveer 2,5 cm.
c. De afstand van B tot de x-as is 3 cm en de afstand van B tot de y-as is 2 cm.

18.
Tip:
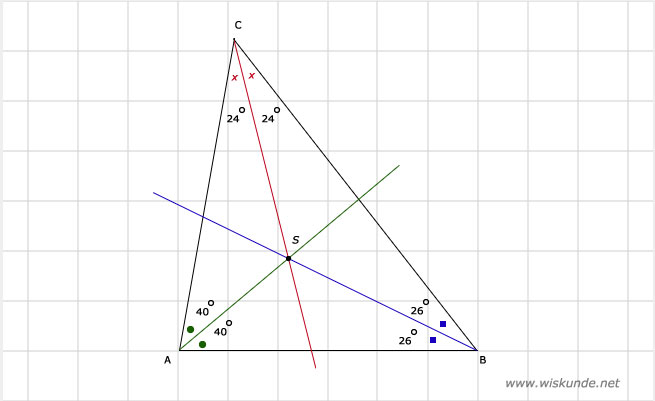
De bissectrice deelt hoek A in 2 gelijke hoeken van 40º. Dit geldt natuurlijk ook voor de andere 2 hoeken.
De 3 bissectrices van een driehoek gaan door 1 punt.
a. Zie afbeeldingDe bissectrice deelt hoek A in 2 gelijke hoeken van 40º. Dit geldt natuurlijk ook voor de andere 2 hoeken.
De 3 bissectrices van een driehoek gaan door 1 punt.
b. Ja, dat klopt ook in de tekening.

19.
Tip:
∠A is ongeveer 34º. Dus de beide hoeken gevormd door de deellijn/bissectrice bij A zijn 17º.
a. Zie afbeelding∠A is ongeveer 34º. Dus de beide hoeken gevormd door de deellijn/bissectrice bij A zijn 17º.
b. Rood is de bissectrice van hoek A.
c. Het blauwe punt Q is het snijpunt van de rode bissectrice en de y-as.

20.
Tip:
Als een punt X even ver ligt van de punten Y en Z dan ligt punt X op de middelloodlijn van YZ.
a. Zie afbeeldingAls een punt X even ver ligt van de punten Y en Z dan ligt punt X op de middelloodlijn van YZ.
b. Teken de bissectrice van hoek A. Deze is rood in de afbeelding.
c. Teken de middelloodlijn van AC. Punt Q is snijpunt van de bissectrice en de middelloodlijn.

21.
Tip:
Hoeken met gelijke tekentjes zijn even groot. Bij een hoek waar de bissectrice van is getekend, zetten we dus gelijke tekentjes.
Het gele gebied hoort bij club A. Het groene gebied hoort bij club B. Het witte gebied hoort bij club C.Hoeken met gelijke tekentjes zijn even groot. Bij een hoek waar de bissectrice van is getekend, zetten we dus gelijke tekentjes.

22.
a. Hoe construeer je de bissectrice van een hoek B? Teken eerst een hoek B. Teken dan een cirkel met middelpunt B. Kies zelf een straallengte van de cirkel. Deze cirkel snijdt de benen van de hoek B in de punten C en D.
Teken nu een cirkel met middelpunt C en straal CD. En teken tevens een cirkel met middelpunt D en straal CD. Deze 2 cirkels snijden elkaar in 2 punten. Noem deze punten E en F.
Teken nu de lijn door hoekpunt B, E en F. Deze lijn is de bissectrice van hoek B.
b. Zie afbeelding

23.
Tip:
Bij b: Construeer de bissectrices met je passer. Dus niet de hoeken opmeten en dan in 2 stukken verdelen.
a. Zie afbeeldingBij b: Construeer de bissectrices met je passer. Dus niet de hoeken opmeten en dan in 2 stukken verdelen.
b. Zie afbeelding. Let wel: construeer is met je passer. Je mag dus niet opmeten!
c. Omdat M het middelpunt is van de ingeschreven cirkel. En de straal die loodrecht op de zijde staat, is de afstand van M tot die zijde. Deze 3 afstanden zijn steeds gelijk (gelijk aan r).
d. *
e. De afstand (d) van middelpunt tot zijde AB is ongeveer 1,5 cm.
f. Zie de rode cirkel

24.
Tip:
Blauwe cirkel: een cirkel met middelpunt A en straal is 5
Groene cirkel: een cirkel met middelpunt B en straal is 9
Het snijpunt van deze 2 cirkels is punt C.
a. Zie afbeeldingBlauwe cirkel: een cirkel met middelpunt A en straal is 5
Groene cirkel: een cirkel met middelpunt B en straal is 9
Het snijpunt van deze 2 cirkels is punt C.
b. Zie afbeelding
c. volgt *

25.
Tip:
∠A1 = 1/2 x 62º = 31º
∠B2 = 1/2 x 48º = 24º
a. ∠C = 180º - 62º - 48º = 70º∠A1 = 1/2 x 62º = 31º
∠B2 = 1/2 x 48º = 24º
b. ∠D1 = 180º - 48º - 31º = 101º
c. ∠E2 = 180º - 24º - 70º = 86º
26.
Tip:
Een gestrekte hoek is 180º
De bissectrice deelt de hoek in 2 gelijke hoeken (bijvoorbeeld ∠R1 en ∠R2)
Bereken ∠M1:Een gestrekte hoek is 180º
De bissectrice deelt de hoek in 2 gelijke hoeken (bijvoorbeeld ∠R1 en ∠R2)
∠R = 180º - 44º - 38º = 98º
∠R1 = 1/2 x 98º = 49º
∠P1 + ∠M1 + ∠R1 = 180º
∠M1 = 180º - 22º - 49º
∠M1 = 109º
Bereken ∠S2:
∠P2 + ∠Q + ∠S2 = 180º
∠S2 = 180º - 22º - 38º
∠S2 = 120º
27.
∠E1 = 180º - ∠B1 - ∠A
∠E1 = 180º - 36º - 42º
∠E1 = 102º
b. ∠F1 = 360º - 36º - 102º - 90º = 132º (hoekensom vierhoek)
∠F2 = 180º - 132º = 48º
c. ∠E4 = 180º - 102º = 78º
∠S1 = 180º - ∠E4 - ∠D
∠S1 = 180º - 78º - 90º = 12º
∠S2 = 180º - 12º = 168º
28.
*
Tip:
∠B1 = 1/2 x 72º = 36º
De hoekensom van een driehoek is 180º
De hoekensom van een vierhoek is 360º
a. ∠A = 180º - 66º - 72º = 42º∠B1 = 1/2 x 72º = 36º
De hoekensom van een driehoek is 180º
De hoekensom van een vierhoek is 360º
∠E1 = 180º - ∠B1 - ∠A
∠E1 = 180º - 36º - 42º
∠E1 = 102º
b. ∠F1 = 360º - 36º - 102º - 90º = 132º (hoekensom vierhoek)
∠F2 = 180º - 132º = 48º
c. ∠E4 = 180º - 102º = 78º
∠S1 = 180º - ∠E4 - ∠D
∠S1 = 180º - 78º - 90º = 12º
∠S2 = 180º - 12º = 168º
28.
*
Andere paragrafen:
2.1. Cirkel en middelloodlijn (1 t/m 16)
2.2. De bissectrice (17 t/m 28)
2.3. Zwaartelijn en hoogtelijn (29 t/m 39)
2.4. De oppervlakte van een driehoek (40 t/m 49)
2.5. De oppervlakte van een vierhoek (50 t/m 70)
2.1. Cirkel en middelloodlijn (1 t/m 16)
2.2. De bissectrice (17 t/m 28)
2.3. Zwaartelijn en hoogtelijn (29 t/m 39)
2.4. De oppervlakte van een driehoek (40 t/m 49)
2.5. De oppervlakte van een vierhoek (50 t/m 70)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


