TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 2.3 Zwaartelijn en hoogtelijn VWO 2
Boek: Getal & Ruimte - Vlakke figuren VWO 2 (deel 1) opgaven 29 t/m 39, 2009Wat is een zwaartelijn en een hoogtelijn?
Een zwaartelijn van een hoek is een lijn die door een hoekpunt gaat en de overstaande zijde in 2 gelijke stukken verdeelt.
Zo heeft een driehoek dus altijd 3 zwaartelijnen. Deze 3 zwaartelijnen snijden elkaar in het zwaartepunt.
Een hoogtelijn horende bij een driehoek is een lijn uit een hoekpunt die loodrecht staat op de overstaande zijde.
Een zwaartelijn van een hoek is een lijn die door een hoekpunt gaat en de overstaande zijde in 2 gelijke stukken verdeelt.
Zo heeft een driehoek dus altijd 3 zwaartelijnen. Deze 3 zwaartelijnen snijden elkaar in het zwaartepunt.
Een hoogtelijn horende bij een driehoek is een lijn uit een hoekpunt die loodrecht staat op de overstaande zijde.
29.
30.
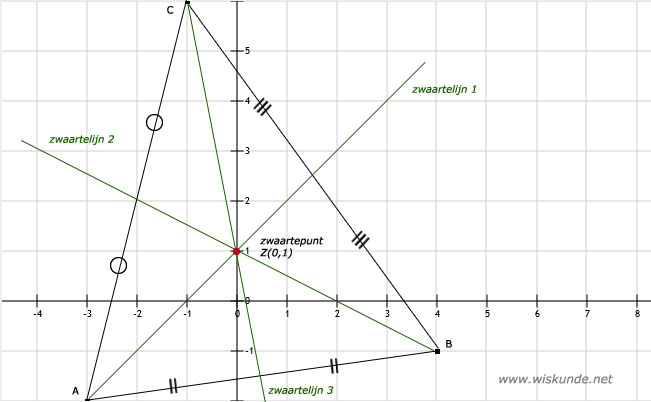
31.
a. Zie afbeelding (let op de schaal is met 2 cm)
b. *
c. Punt E is (0,-5)
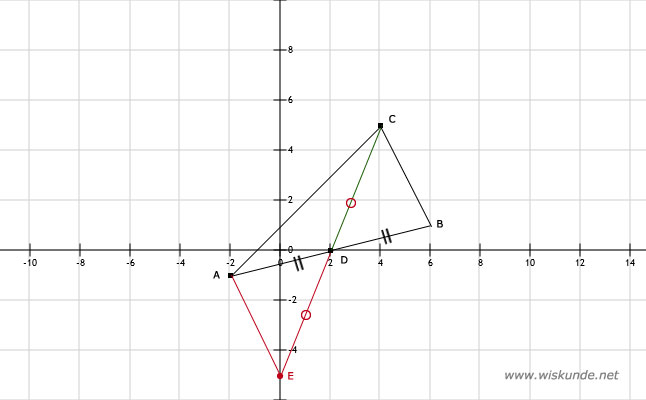
32.
Omdat RS de zwaartelijn is, deelt RS lijnstuk PQ in 2 gelijke stukken. Teken daarna Cirkel(P,4) en teken een Cirkel(S,4,5). Snijpunt deze 2 cirkels is R. Teken daarna QR.
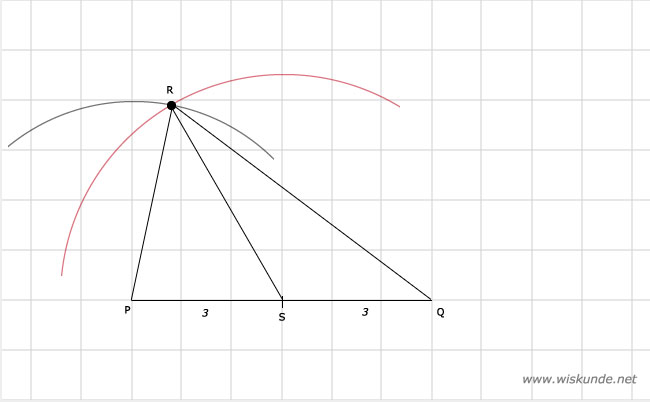
33.
*
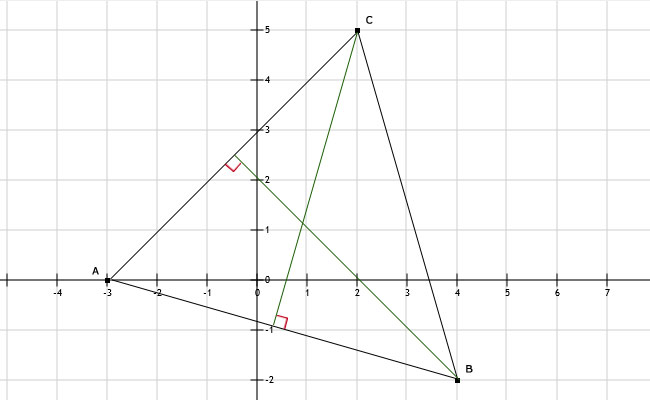
34.
b. De 2 hoogtelijnen zijn groen getekend. Let ook op de rode winkelhaak. Hierdoor weet je zeker dat het de hoogtelijnen zijn.
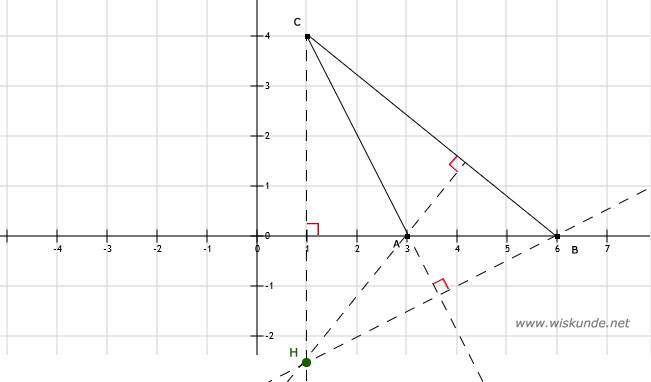
35.
b. *
c. De 3 hoogtelijnen gaan door 1 punt.
Punt H(1 ; -2,5).
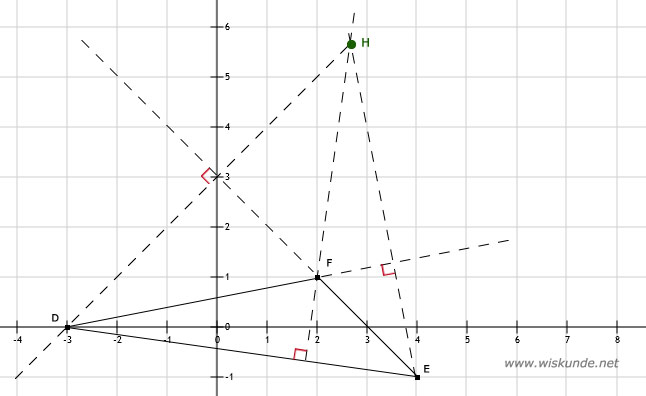
36.
a. Zie afbeelding
b. *
c. Zie het groene punt H.
37.
132º / 2 = 66º
Dus ∠A = ∠B = 66º
∠A2 = 180º - ∠C - ∠D
∠A2 = 180º - 48º - 90º
∠A2 = 42º
∠A1 = 66º - 42º = 24º
38.
a. AD is een hoogtelijn want AD staat loodrecht op BC.
BE is de bissectrice van ∠B.
b. ∠B = 180º - 50º - 90º = 40º (in driehoek ABD)
∠B1 = ∠B2 = 40º / 2 = 20º
∠S3 = 180º - 90º - 20º
∠S3 = 70º
∠C + ∠B + ∠A = 180º
∠A = 180º - 40º - 65º = 75º
∠E1 = 180º - ∠B1 - ∠A
∠E1 = 180º - 20º - 75º = 85º
Tip:
Een zwaartelijn maakt de stukken even zwaar.
Tekening a geeft de bissectrice, b gaat niet door hoek C. Het goede antwoord is tekening c.Een zwaartelijn maakt de stukken even zwaar.
30.
Tip:
De 3 zwaartelijnen van een driehoek gaan door het zwaartepunt. Plaats een spijker onder het zwaartepunt en de driehoek blijft dan mooi balanceren.
Zie afbeeldingDe 3 zwaartelijnen van een driehoek gaan door het zwaartepunt. Plaats een spijker onder het zwaartepunt en de driehoek blijft dan mooi balanceren.

31.
a. Zie afbeelding (let op de schaal is met 2 cm)
b. *
c. Punt E is (0,-5)

32.
Omdat RS de zwaartelijn is, deelt RS lijnstuk PQ in 2 gelijke stukken. Teken daarna Cirkel(P,4) en teken een Cirkel(S,4,5). Snijpunt deze 2 cirkels is R. Teken daarna QR.

33.
*
34.
Tip:
De hoogtelijn uit een punt A is een lijn door het punt A die loodrecht staat op de overstaande zijde van punt A.
a. Zie afbeeldingDe hoogtelijn uit een punt A is een lijn door het punt A die loodrecht staat op de overstaande zijde van punt A.
b. De 2 hoogtelijnen zijn groen getekend. Let ook op de rode winkelhaak. Hierdoor weet je zeker dat het de hoogtelijnen zijn.

35.
Tip:
In elke driehoek gaan de 3 hoogtelijnen door 1 punt. We noemen dit punt het hoogtepunt.
a. Zie afbeeldingIn elke driehoek gaan de 3 hoogtelijnen door 1 punt. We noemen dit punt het hoogtepunt.
b. *
c. De 3 hoogtelijnen gaan door 1 punt.
Punt H(1 ; -2,5).

36.
a. Zie afbeelding
b. *
c. Zie het groene punt H.

37.
Tip:
In een gelijkbenige driehoek zijn de basishoeken even groot.
180º - 48º = 132ºIn een gelijkbenige driehoek zijn de basishoeken even groot.
132º / 2 = 66º
Dus ∠A = ∠B = 66º
∠A2 = 180º - ∠C - ∠D
∠A2 = 180º - 48º - 90º
∠A2 = 42º
∠A1 = 66º - 42º = 24º
38.
a. AD is een hoogtelijn want AD staat loodrecht op BC.
BE is de bissectrice van ∠B.
b. ∠B = 180º - 50º - 90º = 40º (in driehoek ABD)
∠B1 = ∠B2 = 40º / 2 = 20º
∠S3 = 180º - 90º - 20º
∠S3 = 70º
∠C + ∠B + ∠A = 180º
∠A = 180º - 40º - 65º = 75º
∠E1 = 180º - ∠B1 - ∠A
∠E1 = 180º - 20º - 75º = 85º
39.
∠Q12 = 180º - 30º - 90º = 60º (in driehoek RUQ)
∠H1 = 180º - ∠S - ∠Q12
∠H1 = 180º - 90º - 60º
∠H1 = 30º
∠Q2 = 60º - 25º = 35º
∠H12 = 180º - ∠T - ∠Q2
∠H12 = 180º - 90º - 35º = 55º
∠H2 = 55º - 30º = 25º
∠Q12 = 180º - 30º - 90º = 60º (in driehoek RUQ)
∠H1 = 180º - ∠S - ∠Q12
∠H1 = 180º - 90º - 60º
∠H1 = 30º
∠Q2 = 60º - 25º = 35º
∠H12 = 180º - ∠T - ∠Q2
∠H12 = 180º - 90º - 35º = 55º
∠H2 = 55º - 30º = 25º
Andere paragrafen:
2.1. Cirkel en middelloodlijn (1 t/m 16)
2.2. De bissectrice (17 t/m 28)
2.3. Zwaartelijn en hoogtelijn (29 t/m 39)
2.4. De oppervlakte van een driehoek (40 t/m 49)
2.5. De oppervlakte van een vierhoek (50 t/m 70)
2.1. Cirkel en middelloodlijn (1 t/m 16)
2.2. De bissectrice (17 t/m 28)
2.3. Zwaartelijn en hoogtelijn (29 t/m 39)
2.4. De oppervlakte van een driehoek (40 t/m 49)
2.5. De oppervlakte van een vierhoek (50 t/m 70)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


