TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 2.5 De oppervlakte van een vierhoek VWO 2
Boek: Getal & Ruimte - Vlakke figuren VWO 2 (deel 1) opgaven 50 t/m 70, 2009Een parallellogram is een figuur met 2 paar overstaande evenwijdige zijden.
- oppervlakte parallellogram = zijde x bijbehorende hoogte
Een trapezium is een figuur met maar 1 paar overstaande evenwijdige zijden.
- oppervlakte trapezium = 1/2 x som van de evenwijdige zijden x hoogte = 1/2 x (a + b) x h
- oppervlakte parallellogram = zijde x bijbehorende hoogte
Een trapezium is een figuur met maar 1 paar overstaande evenwijdige zijden.
- oppervlakte trapezium = 1/2 x som van de evenwijdige zijden x hoogte = 1/2 x (a + b) x h
50.
b. Verschuif horizontaal de hoogtelijn uit S met hoogte gelijk aan 3 naar het punt Q. Dan is deze hoogte (h = 3) ook de hoogte van driehoek QRS. En de basis horende bij driehoek QRS is RS. Dus opp(QRS) = 1/2 x 5 x 3 = 7,5.
c. Oppervlakte is 2 x (1/2 x zijde x bijbehorende hoogte) = zijde x bijbehorende hoogte
51.
a. De hoogte die hoort bij AB is: DE = 25
b. De hoogte die hoort bij AD is: DF = 49
c. De hoogte die hoort bij CD is: DE = 25
d. BC staat niet loodrecht op AB.
52.
opp(KLMN) = ML x KS
opp(KLMN) = 29 x 43
opp(KLMN) = 1247 mm2
53.
opp(parallellogram I ) = AB x CP = 25 x 13 = 325 mm2
opp(parallellogram II ) = FG x HQ = 18 x 16 = 288 mm2
opp(parallellogram III) = MN x MR = 15 x 12 = 180 mm2
54.
a.
opp(rood) = 3 x 7 = 21
opp(blauw) = 3 x 7 = 21
opp(groen) = 3 x 7 = 21
b. Oppervlakte van elk parallellogram is gelijk, dat komt omdat ze allemaal dezelfde zijde hebben (van 3) en allemaal een hoogte van 7.
c. Kleinste omtrek heeft de blauwe en de grootste omtrek heeft de groene.
55.
56.
a. Zie afbeelding
b. *
c. *
d. We kennen de lengte van AB (die is 5) en de bijbehorende hoogte van AB is gelijk aan 3.
Oppervlakte van ABCD = 5 x 3 = 15 cm2
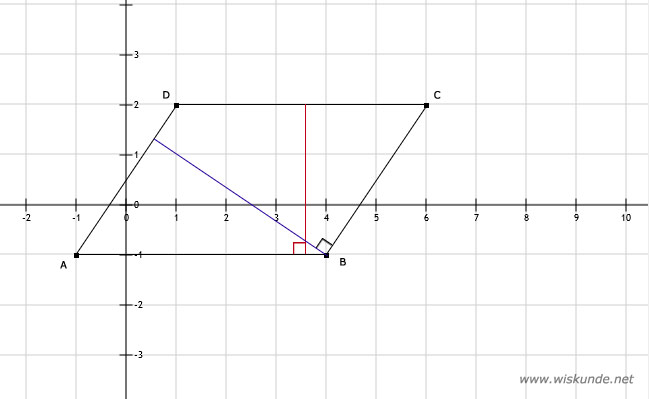
57.
a. Zie afbeelding. Punt D(-2,4) is het vierde hoekpunt. Opp(ABCD) = AD x h = 3 x 5 = 15 cm2
b. Punt E(-2,-2) is het vierde hoekpunt.
opp(AEBC) = AE x h = 3 x 5 = 15 cm2
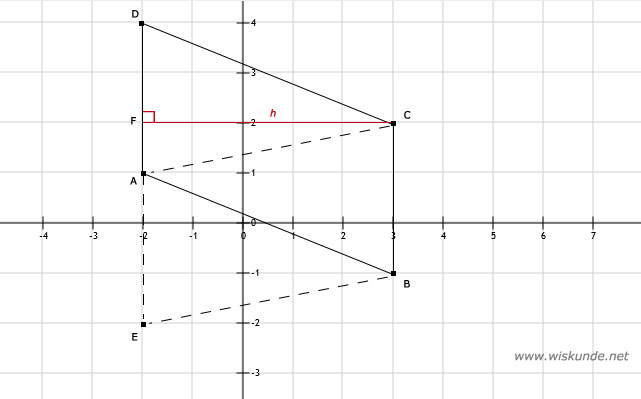
58.
oppervlakte parallellogram(ABCD) = zijde x bijbehorende hoogte
Invullen wat je weet:
28 = 4 x h
h = 7
b.
oppervlakte parallellogram(KLMN) = zijde x bijbehorende hoogte
Invullen wat je weet:
48 = 16 x h
h = 3
c.
oppmanier1(PQRS) = PQ x SU = 4 x 2,4 = 9,6
oppmanier2(PQRS) = QR x ST
9,6 = 3 x ST
ST = 3,2
d.
oppmanier1(EFGH) = 8 x 4,2 = 33,6
oppmanier2(EFGH) = FG x h
33,6 = 5 x h
h = 33,6 / 5 = 6,72
e. Maak een schets. Je ziet dat h = 4. Dan is het snijpunt met de y-as: C(0,-1) of C(0,7). Dan geldt voor punt D: D(-6,-1) of D(-6,7)
59.
opp(PQS) = 1/2 x zijde x bijbehorende hoogte
opp(PQS) = 1/2 x 6 x 3
opp(PQS) = 9
b.
opp(QRS) = 1/2 x zijde x bijbehorende hoogte
opp(QRS) = 1/2 x 2,8 x 3
opp(QRS) = 4,2
c.
opp(PQRS) = 9 + 4,2 = 13,2
Tip:
Bij een parallellogram zijn de overstaande zijden even lang. Dus PQ en RS zijn even lang.
a. opp(PQS) = 1/2 x zijde x bijbehorende hoogte = 1/2 x 5 x 3 = 7,5Bij een parallellogram zijn de overstaande zijden even lang. Dus PQ en RS zijn even lang.
b. Verschuif horizontaal de hoogtelijn uit S met hoogte gelijk aan 3 naar het punt Q. Dan is deze hoogte (h = 3) ook de hoogte van driehoek QRS. En de basis horende bij driehoek QRS is RS. Dus opp(QRS) = 1/2 x 5 x 3 = 7,5.
c. Oppervlakte is 2 x (1/2 x zijde x bijbehorende hoogte) = zijde x bijbehorende hoogte
51.
a. De hoogte die hoort bij AB is: DE = 25
b. De hoogte die hoort bij AD is: DF = 49
c. De hoogte die hoort bij CD is: DE = 25
d. BC staat niet loodrecht op AB.
52.
Tip:
Je weet niet hoelang KL of MN is. Zoek dus een andere zijde en de bijbehorende hoogte.
Bedenk: ML = NK
oppervlakte parallellogram KLMN = zijde x bijbehorende hoogteJe weet niet hoelang KL of MN is. Zoek dus een andere zijde en de bijbehorende hoogte.
Bedenk: ML = NK
opp(KLMN) = ML x KS
opp(KLMN) = 29 x 43
opp(KLMN) = 1247 mm2
53.
opp(parallellogram I ) = AB x CP = 25 x 13 = 325 mm2
opp(parallellogram II ) = FG x HQ = 18 x 16 = 288 mm2
opp(parallellogram III) = MN x MR = 15 x 12 = 180 mm2
54.
a.
opp(rood) = 3 x 7 = 21
opp(blauw) = 3 x 7 = 21
opp(groen) = 3 x 7 = 21
b. Oppervlakte van elk parallellogram is gelijk, dat komt omdat ze allemaal dezelfde zijde hebben (van 3) en allemaal een hoogte van 7.
c. Kleinste omtrek heeft de blauwe en de grootste omtrek heeft de groene.
55.
Tip:
Een rechthoek is een bijzonder parallellogram. Een rechthoek heeft alle eigenschappen van een parallellogram.
Maak een rechthoek van 6 x 2 spijkers. De oppervlakte is dan 6 x 2 = 12 en de omtrek is 6 + 2 + 6 + 2 = 16.Een rechthoek is een bijzonder parallellogram. Een rechthoek heeft alle eigenschappen van een parallellogram.
56.
a. Zie afbeelding
b. *
c. *
d. We kennen de lengte van AB (die is 5) en de bijbehorende hoogte van AB is gelijk aan 3.
Oppervlakte van ABCD = 5 x 3 = 15 cm2

57.
a. Zie afbeelding. Punt D(-2,4) is het vierde hoekpunt. Opp(ABCD) = AD x h = 3 x 5 = 15 cm2
b. Punt E(-2,-2) is het vierde hoekpunt.
opp(AEBC) = AE x h = 3 x 5 = 15 cm2

58.
Tip:
Maak bij de volgende opgaven eerst een schets. Dan zie je het beter.
a. Maak bij de volgende opgaven eerst een schets. Dan zie je het beter.
oppervlakte parallellogram(ABCD) = zijde x bijbehorende hoogte
Invullen wat je weet:
28 = 4 x h
h = 7
b.
oppervlakte parallellogram(KLMN) = zijde x bijbehorende hoogte
Invullen wat je weet:
48 = 16 x h
h = 3
c.
oppmanier1(PQRS) = PQ x SU = 4 x 2,4 = 9,6
oppmanier2(PQRS) = QR x ST
9,6 = 3 x ST
ST = 3,2
d.
oppmanier1(EFGH) = 8 x 4,2 = 33,6
oppmanier2(EFGH) = FG x h
33,6 = 5 x h
h = 33,6 / 5 = 6,72
e. Maak een schets. Je ziet dat h = 4. Dan is het snijpunt met de y-as: C(0,-1) of C(0,7). Dan geldt voor punt D: D(-6,-1) of D(-6,7)
59.
Tip:
oppervlakte driehoek = 1/2 x zijde x bijbehorende hoogte
a.oppervlakte driehoek = 1/2 x zijde x bijbehorende hoogte
opp(PQS) = 1/2 x zijde x bijbehorende hoogte
opp(PQS) = 1/2 x 6 x 3
opp(PQS) = 9
b.
opp(QRS) = 1/2 x zijde x bijbehorende hoogte
opp(QRS) = 1/2 x 2,8 x 3
opp(QRS) = 4,2
c.
opp(PQRS) = 9 + 4,2 = 13,2
60.
b. oppervlakte trapezium PQRS = 1/2 x (a + b) x h = 1/2 x (1 + 5) x 2,5 = 3 x 2,5 = 7,5
61.
108 000 x 2,588881 = 279 599 km2
62.
opp(bucket) = 1/2 x (3,6 + 6) x 5,8
opp(bucket) = 27,84 m2
63.
68 = 1/2 x (6 + 10) x h
68 = 8 x h
h = 8,5
b. opp(PQRS) = 1/2 x (a + b) x h
33,75 = 1/2 x (PS + 8) x 2,5
33,75 = 1,25 x (PS + 8)
33,75 = 1,25PS + 10
1,25PS = 23,75
PS = 19
64.
opp(driehoek) = 1/2 x zijde x bijbehorende hoogte = 1/2 x 12 x 8 = 48
opp(dak) = 2 x 128 + 2 x 48 = 352 m2
65.
opp(figuur b) = 350 mm2
opp(figuur c) = 770 mm2
66.
100 x 2 = 200 m2
200 / 10 x 80 = 1600,=
67.
opp(ABC) = 1/2 x AC x BS = 1/2 x 48 x 11 = 264
Dus: opp(ABCD) = 264 + 264 = 528
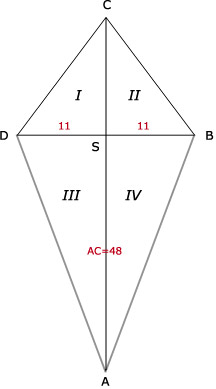
68.
opp(ABCD) = opp(ABD) + opp(BCD)
opp(ABCD) = 1/2 x BD x AS + 1/2 x BD x CS
Nu '1/2 x BD' voor de haakjes halen:
opp(ABCD) = 1/2 x BD x (AS + CS)
opp(ABCD) = 1/2 x BD x AC
opp(ABCD) = 1/2 x diagonaal1 x diagonaal2
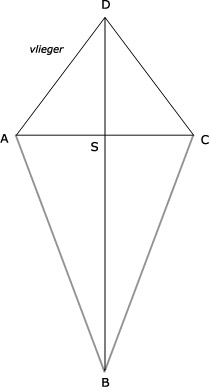
69.
a.
opp(ABCD) = 1/2 ⋅ (a + b) ⋅ h
opp(ABCD) = 1/2 ⋅ (2x + 4x) ⋅ 3x
opp(ABCD) = (x + 2x) ⋅ 3x
opp(ABCD) = 3x ⋅ 3x
opp(ABCD) = 9x2
b.
opp(EFGH) = zijde ⋅ bijbehorende hoogte
opp(EFGH) = 2x ⋅ 3x
opp(EFGH) = 6x2
c.
opp(PQRS) = 1/2 ⋅ d1 ⋅ d2
opp(PQRS) = 1/2 ⋅ 2x ⋅ 4x
opp(PQRS) = 4x2
Tip:
oppervlakte trapezium = 1/2 x (a + b) x h
a. oppervlakte trapezium ABCD = 1/2 x (a + b) x h = 1/2 x (2 + 4) x 2,5 = 3 x 2,5 = 7,5oppervlakte trapezium = 1/2 x (a + b) x h
b. oppervlakte trapezium PQRS = 1/2 x (a + b) x h = 1/2 x (1 + 5) x 2,5 = 3 x 2,5 = 7,5
61.
Tip:
1 mijl = 1,609 km
1 mijl2 = 1,6092 = 2,588881 km2
Of? Je kan ook eerst alles omrekenen naar km.
opp(nevada) = 1/2 x (475 + 200) x 320 = 108 000 mijl21 mijl = 1,609 km
1 mijl2 = 1,6092 = 2,588881 km2
Of? Je kan ook eerst alles omrekenen naar km.
108 000 x 2,588881 = 279 599 km2
62.
Tip:
De straal van de cirkel is: r = 1,8. Dus de diameter is 2 x 1,8 = 3,6
En de diameter is de 'a' die hoort bij de formule: 1/2 x (a + b) x h
opp(bucket) = 1/2 x (a + b) x hDe straal van de cirkel is: r = 1,8. Dus de diameter is 2 x 1,8 = 3,6
En de diameter is de 'a' die hoort bij de formule: 1/2 x (a + b) x h
opp(bucket) = 1/2 x (3,6 + 6) x 5,8
opp(bucket) = 27,84 m2
63.
Tip:
Maak eerst een schets, schrijf de formule op en vul in wat je weet!
a.
opp(ABCD) = 1/2 x (a + b) x hMaak eerst een schets, schrijf de formule op en vul in wat je weet!
68 = 1/2 x (6 + 10) x h
68 = 8 x h
h = 8,5
b. opp(PQRS) = 1/2 x (a + b) x h
33,75 = 1/2 x (PS + 8) x 2,5
33,75 = 1,25 x (PS + 8)
33,75 = 1,25PS + 10
1,25PS = 23,75
PS = 19
64.
Tip:
oppervlakte(dak) = 2 x oppervlakte(trapezium) + 2 x oppervlakte(driehoek)
opp(trapezium) = 1/2 x (a + b) x h = 1/2 x (10 + 22) x 8 = 128oppervlakte(dak) = 2 x oppervlakte(trapezium) + 2 x oppervlakte(driehoek)
opp(driehoek) = 1/2 x zijde x bijbehorende hoogte = 1/2 x 12 x 8 = 48
opp(dak) = 2 x 128 + 2 x 48 = 352 m2
65.
Tip:
figuur a = rechthoek - driehoek
figuur b = binnen rechthoek (20x14) + 2 driehoeken
figuur c = rechthoek + driehoek
opp(figuur a) = 898 mm2figuur a = rechthoek - driehoek
figuur b = binnen rechthoek (20x14) + 2 driehoeken
figuur c = rechthoek + driehoek
opp(figuur b) = 350 mm2
opp(figuur c) = 770 mm2
66.
Tip:
Het pad bestaat uit 100 parallellogrammen. Pak 1 parallellogram eruit. Deze is 1 m breed en heeft een hoogte van 2 m.
Oppervlakte 1 parallellogram = zijde x bijbehorende hoogte = 1 x 2 = 2 m2Het pad bestaat uit 100 parallellogrammen. Pak 1 parallellogram eruit. Deze is 1 m breed en heeft een hoogte van 2 m.
100 x 2 = 200 m2
200 / 10 x 80 = 1600,=
67.
Tip:
oppervlakte vlieger ABCD = oppervlakte driehoek ACD + oppervlakte driehoek ABC
opp(ACD) = 1/2 x AC x DS = 1/2 x 48 x 11 = 264oppervlakte vlieger ABCD = oppervlakte driehoek ACD + oppervlakte driehoek ABC
opp(ABC) = 1/2 x AC x BS = 1/2 x 48 x 11 = 264
Dus: opp(ABCD) = 264 + 264 = 528

68.
opp(ABCD) = opp(ABD) + opp(BCD)
opp(ABCD) = 1/2 x BD x AS + 1/2 x BD x CS
Nu '1/2 x BD' voor de haakjes halen:
opp(ABCD) = 1/2 x BD x (AS + CS)
opp(ABCD) = 1/2 x BD x AC
opp(ABCD) = 1/2 x diagonaal1 x diagonaal2

69.
a.
opp(ABCD) = 1/2 ⋅ (a + b) ⋅ h
opp(ABCD) = 1/2 ⋅ (2x + 4x) ⋅ 3x
opp(ABCD) = (x + 2x) ⋅ 3x
opp(ABCD) = 3x ⋅ 3x
opp(ABCD) = 9x2
b.
opp(EFGH) = zijde ⋅ bijbehorende hoogte
opp(EFGH) = 2x ⋅ 3x
opp(EFGH) = 6x2
c.
opp(PQRS) = 1/2 ⋅ d1 ⋅ d2
opp(PQRS) = 1/2 ⋅ 2x ⋅ 4x
opp(PQRS) = 4x2
70.
*
*
Andere paragrafen:
2.1. Cirkel en middelloodlijn (1 t/m 16)
2.2. De bissectrice (17 t/m 28)
2.3. Zwaartelijn en hoogtelijn (29 t/m 39)
2.4. De oppervlakte van een driehoek (40 t/m 49)
2.5. De oppervlakte van een vierhoek (50 t/m 70)
2.1. Cirkel en middelloodlijn (1 t/m 16)
2.2. De bissectrice (17 t/m 28)
2.3. Zwaartelijn en hoogtelijn (29 t/m 39)
2.4. De oppervlakte van een driehoek (40 t/m 49)
2.5. De oppervlakte van een vierhoek (50 t/m 70)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


