TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 2.1 Cirkel en middelloodlijn VWO 2
Boek: Getal & Ruimte - Vlakke figuren VWO 2 (deel 1) opgaven 1 t/m 16, 2009Een cirkel is een plat figuur die bestaat uit alle punten die een gelijke afstand hebben tot een bepaald punt.
Dit punt noemen we het middelpunt van de cirkel. Deze geven we vaak aan met M.
Een cirkel met C(M,3) betekent dat de cirkel een middelpunt M heeft en de straal gelijk is aan 3.
De omgeschreven cirkel van een driehoek gaat door de 3 hoekpunten van de driehoek.
De middelloodlijn van een lijnstuk is een rechte lijn die door het midden van dit lijnstuk gaat en loodrecht op dat lijnstuk staat.
Dit punt noemen we het middelpunt van de cirkel. Deze geven we vaak aan met M.
Een cirkel met C(M,3) betekent dat de cirkel een middelpunt M heeft en de straal gelijk is aan 3.
De omgeschreven cirkel van een driehoek gaat door de 3 hoekpunten van de driehoek.
De middelloodlijn van een lijnstuk is een rechte lijn die door het midden van dit lijnstuk gaat en loodrecht op dat lijnstuk staat.
1.
b. Zie getekende kleine cirkel in de afbeelding.
c. Zie afbeelding, in het rode gebied kun je beide zenders ontvangen.
d. Zie blauwe cirkel (met stukje rood eraf) in de afbeelding.
2.
b. Zie rode gebied in de afbeelding. Rood is het gebied dat buiten de cirkel D met straal 4 valt en binnen de cirkel E met straal 3.
c. Zie 2 blauwe stippen in de afbeelding. Dat zijn de snijpunten van de 2 cirkels: PD = 4 en PE = 3.
3.
b. Zie groene cirkelboog in de afbeelding. Ofwel: buiten de kleine cirkel en op de rand van de grote cirkel.
4.
b. Dat is de grootste cirkel met middelpunt C en straal is 5. Dus cirkel(C,5).
c. Die punten bestaan niet. Punten kunnen niet zowel buiten de grote cirkel EN binnen de kleine cirkel liggen.
d. a is dan maximaal 5.
5.
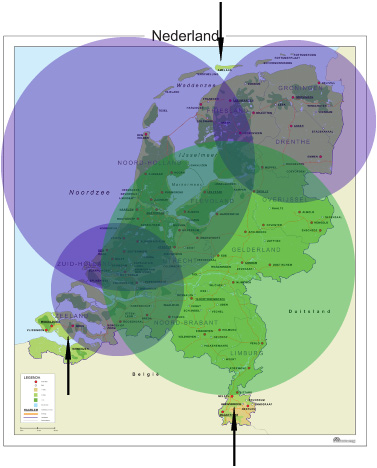
a. Zie afbeelding. De gebieden met de zwarte pijlen zijn niet te bereiken. De cirkels zijn gebieden waar een helikopter kan komen. Waar geen cirkel ligt, is het gebied niet bereikbaar.
b. Dat is de groene cirkel, die niet met een paarse cirkel overlapt.
6.
Zie afbeelding
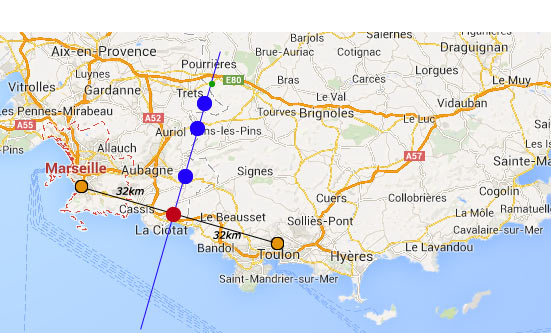
7.
a. Zie afbeelding
b. De middelloodlijn van AB is groen.
c. Teken een cirkel met middelpunt C en straal is 2 (rood). Deze rode cirkel snijdt de groene middelloodlijn in 2 blauwe punten.
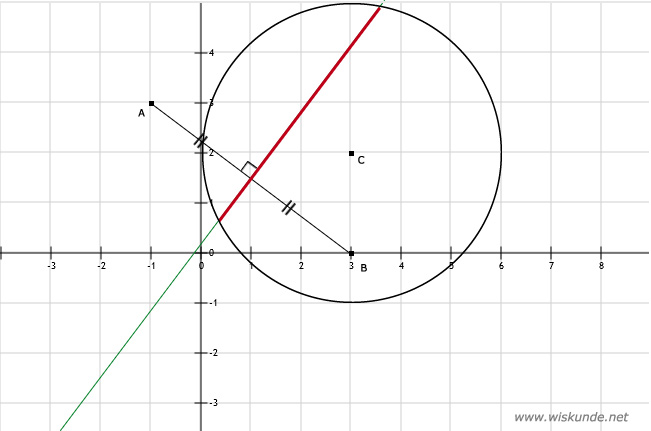
8.
b. Teken eerst de middelloodlijn (groen) van AB, want hierop liggen de punten die gelijke afstand hebben van A en B. Teken daarna de cirkel met middelpunt C en straal is 3. De punten op het rode lijnstuk liggen zowel op de groene middelloodlijn als binnen de cirkel.
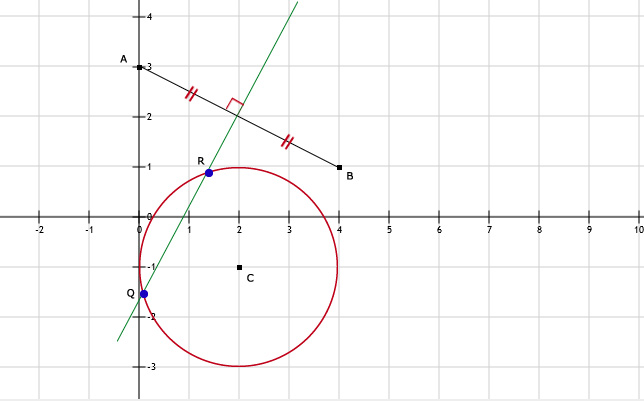
9.
a. Zie afbeelding bij b.
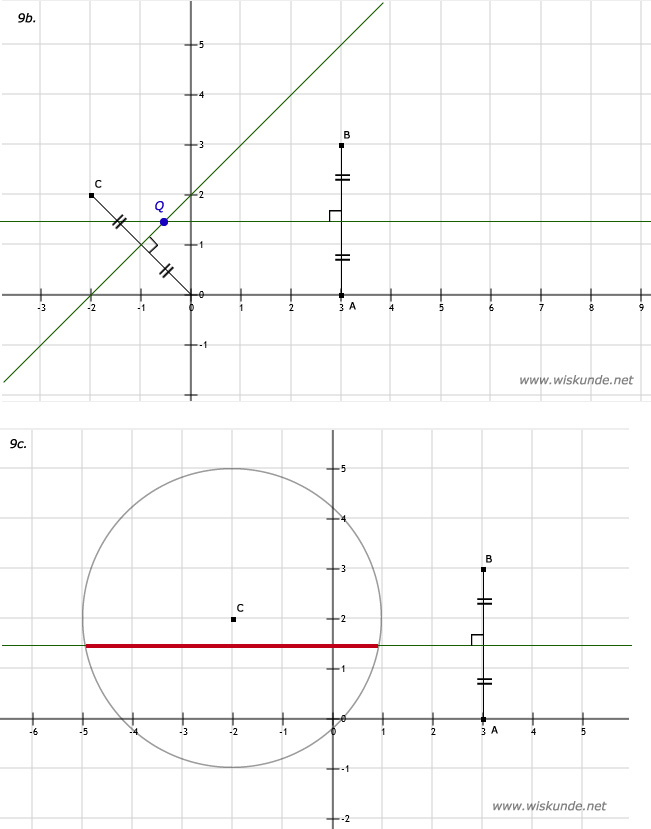
b. Teken de middelloodlijn van AB en teken de middelloodlijn van OC.
Het snijpunt is het gevraagde blauwe punt Q.
c. Rood is de lijn van alle punten die op de middelloodlijn liggen van AB en binnen de cirkel met middelpunt C en straal is 3.
10.
Teken de middelloodlijn die ligt op lijnstuk Athene - Olympia en teken de middelloodlijn die ligt op lijnstuk Dion - Dodoni. Het snijpunt van deze 2 middelloodlijnen is het gevraagde punt Delphi.
Tip:
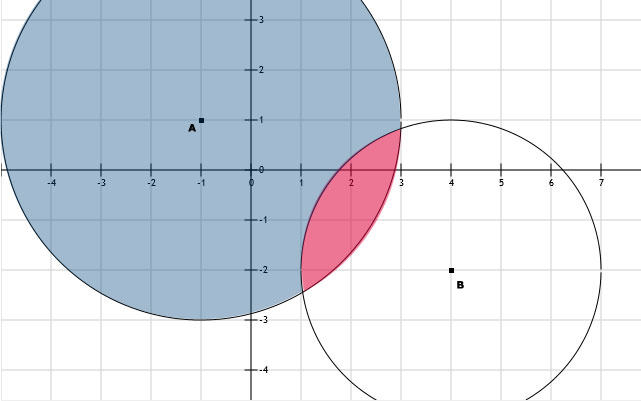
Rood is het gebied met alle punten P waarvoor geldt dat de afstand tot B kleiner is dan 3 EN de afstand tot A kleiner is dan 4. Ofwel: rood is het gebied dat binnen beide cirkels ligt (overlapping).
a. Zie getekende grote cirkel in de afbeelding.Rood is het gebied met alle punten P waarvoor geldt dat de afstand tot B kleiner is dan 3 EN de afstand tot A kleiner is dan 4. Ofwel: rood is het gebied dat binnen beide cirkels ligt (overlapping).
b. Zie getekende kleine cirkel in de afbeelding.
c. Zie afbeelding, in het rode gebied kun je beide zenders ontvangen.
d. Zie blauwe cirkel (met stukje rood eraf) in de afbeelding.

2.
Tip:
PD > 4 wil zeggen: buiten de cirkel met straal is 4
PE < 3 wil zeggen: binnen de cirkel met straal is 3
Als er zou staan PD ≥ 4 of PE ≤ 3 dan zou de rand van de cirkel ook mee doen.
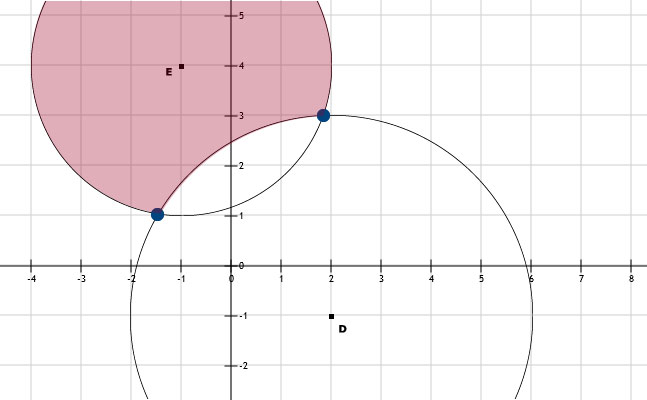
a. Zie afbeeldingPD > 4 wil zeggen: buiten de cirkel met straal is 4
PE < 3 wil zeggen: binnen de cirkel met straal is 3
Als er zou staan PD ≥ 4 of PE ≤ 3 dan zou de rand van de cirkel ook mee doen.
b. Zie rode gebied in de afbeelding. Rood is het gebied dat buiten de cirkel D met straal 4 valt en binnen de cirkel E met straal 3.
c. Zie 2 blauwe stippen in de afbeelding. Dat zijn de snijpunten van de 2 cirkels: PD = 4 en PE = 3.

3.
Tip:
PA < 2 wil zeggen: alles binnen de cirkel met straal 2 en middelpunt A.
PB > 3 wil zeggen: alles buiten de cirkel met straal 3 en middelpunt B.
PB = 3 wil zeggen: alles op de cirkel met straal 3 (rand).
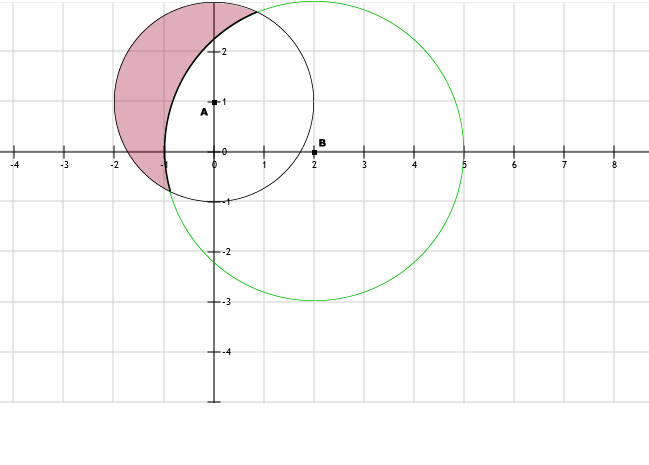
a. Zie rode gebied in de afbeelding. Ofwel: binnen de kleine cirkel en buiten de grote cirkel.PA < 2 wil zeggen: alles binnen de cirkel met straal 2 en middelpunt A.
PB > 3 wil zeggen: alles buiten de cirkel met straal 3 en middelpunt B.
PB = 3 wil zeggen: alles op de cirkel met straal 3 (rand).
b. Zie groene cirkelboog in de afbeelding. Ofwel: buiten de kleine cirkel en op de rand van de grote cirkel.

4.
Tip:
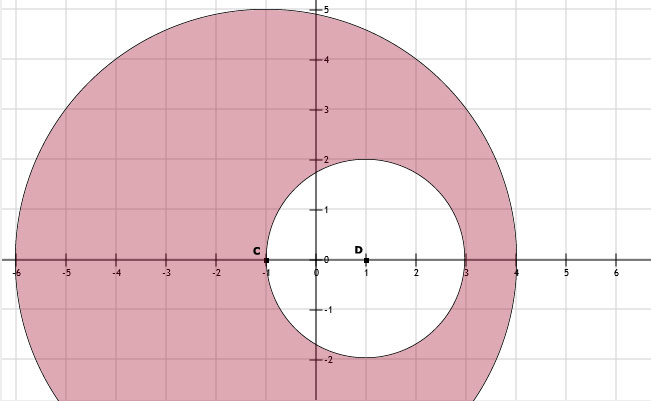
Rood is het gebied binnen de grote cirkel (PC < 5) en buiten de kleine cirkel (PD > 2).
a. Zie afbeeldingRood is het gebied binnen de grote cirkel (PC < 5) en buiten de kleine cirkel (PD > 2).
b. Dat is de grootste cirkel met middelpunt C en straal is 5. Dus cirkel(C,5).
c. Die punten bestaan niet. Punten kunnen niet zowel buiten de grote cirkel EN binnen de kleine cirkel liggen.
d. a is dan maximaal 5.

5.
a. Zie afbeelding. De gebieden met de zwarte pijlen zijn niet te bereiken. De cirkels zijn gebieden waar een helikopter kan komen. Waar geen cirkel ligt, is het gebied niet bereikbaar.
b. Dat is de groene cirkel, die niet met een paarse cirkel overlapt.

6.
Zie afbeelding

7.
a. Zie afbeelding
b. De middelloodlijn van AB is groen.
c. Teken een cirkel met middelpunt C en straal is 2 (rood). Deze rode cirkel snijdt de groene middelloodlijn in 2 blauwe punten.

8.
Tip:
Alle punten die gelijke afstand hebben van A en B liggen op de middelloodlijn van AB.
a. Zie afbeeldingAlle punten die gelijke afstand hebben van A en B liggen op de middelloodlijn van AB.
b. Teken eerst de middelloodlijn (groen) van AB, want hierop liggen de punten die gelijke afstand hebben van A en B. Teken daarna de cirkel met middelpunt C en straal is 3. De punten op het rode lijnstuk liggen zowel op de groene middelloodlijn als binnen de cirkel.

9.
a. Zie afbeelding bij b.
b. Teken de middelloodlijn van AB en teken de middelloodlijn van OC.
Het snijpunt is het gevraagde blauwe punt Q.
c. Rood is de lijn van alle punten die op de middelloodlijn liggen van AB en binnen de cirkel met middelpunt C en straal is 3.

10.
Teken de middelloodlijn die ligt op lijnstuk Athene - Olympia en teken de middelloodlijn die ligt op lijnstuk Dion - Dodoni. Het snijpunt van deze 2 middelloodlijnen is het gevraagde punt Delphi.
11.
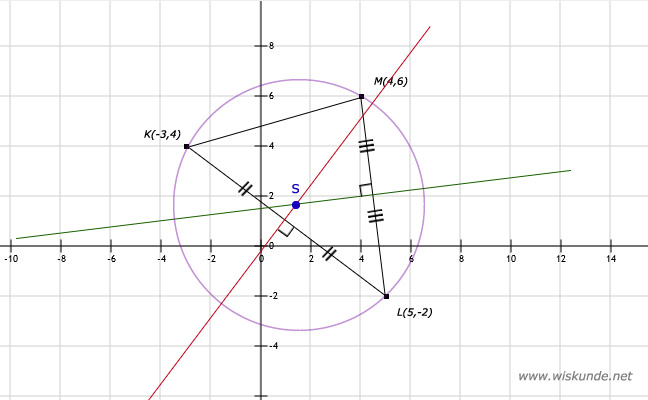
b. Teken de middelloodlijn van KL. Deze is rood in de afbeelding.
c. Teken de middelloodlijn van LM. Deze is groen in de afbeelding.
d. S is het snijpunt van de beide middelloodlijnen. S is blauw in de afbeelding.
e. Zie de paarse cirkel. Zet passerpunt in S en neem straal KS.
12.
a. Zie afbeelding
b. Teken de middelloodlijn van AB en teken de middelloodlijn van BC. Noem het snijpunt van deze 2 middelloodlijnen M. M is het middelpunt van de omgeschreven cirkel. Teken een cirkel met middelpunt M en straal is AM. Je krijgt nu de omgeschreven cirkel.
13.
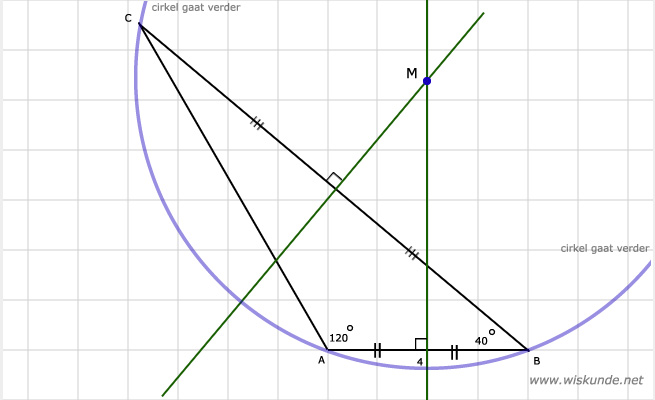
a. Zie afbeelding
b. Teken de middelloodlijn van AB en teken de middelloodlijn van BC. Noem het snijpunt van deze 2 middelloodlijnen M. M is het middelpunt van de omgeschreven cirkel van driehoek ABC. Teken een cirkel met middelpunt M en straal is AM. Je krijgt nu de omgeschreven cirkel.
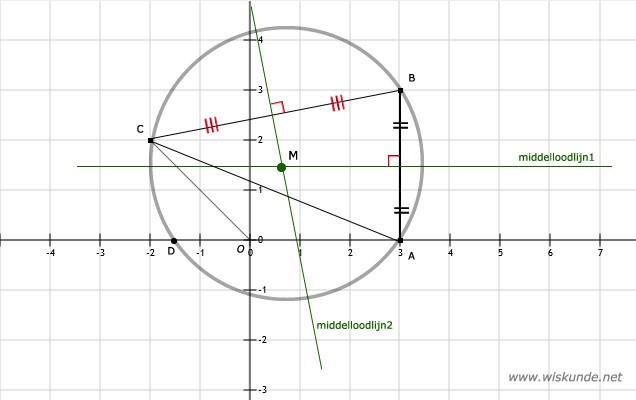
c. Want dan had punt O op de omgeschreven cirkel van driehoek ABC moeten liggen. En dat doet O nu dus niet.
d. Zie afbeelding voor punt D. Deze ligt ongeveer op D(-1,5 ; 0).
14.
a. Zie afbeelding
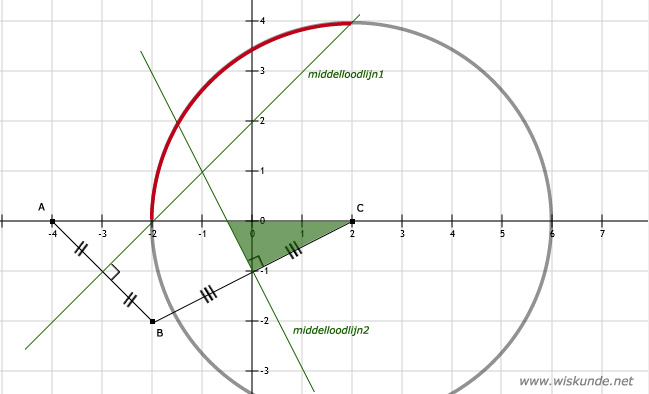
b. Teken eerst een cirkel met middelpunt C en straal is 4. Teken daarna de middelloodlijn van AB. De punten "linksboven" deze middelloodlijn1 liggen dichter bij A dan bij B. Dus teken de cirkelboog rood waar de cirkel linksboven deze middelloodlijn ligt.
c. Teken eerst de middelloodlijn van BC (middelloodlijn2). De gevraagde punten liggen rechts van deze middelloodlijn en binnen de driehoek.
15.
a. Teken een lijnstuk AB. Teken een cirkel met middelpunt A en een straal kleiner dan AB. Teken daarna een cirkel met middelpunt B en dezelfde straal.
Deze 2 cirkels snijden elkaar in 2 punten. Teken een lijn door deze 2 snijpunten. Deze lijn is de middelloodlijn.
b. Je construeert 2 punten met gelijke afstand van zowel A als B. Dus dan liggen deze punten op de middelloodlijn. En je hebt maar 2 punten nodig voor een rechte lijn.
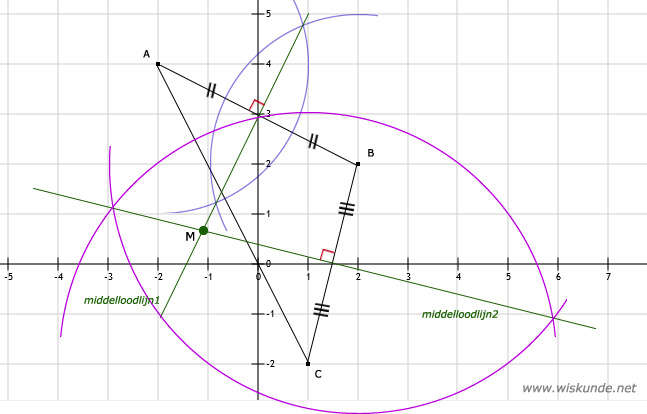
c. Zie afbeelding. Middelpunt omschreven cirkel is snijpunt middelloodlijn 1 en 2.
Deze zit ongeveer op M(-1,25 ; 0,75)
16.
*
Tip:
Om de omgeschreven cirkel van een driehoek te tekenen, hebben we genoeg aan 2 middelloodlijnen.
a. Zie afbeeldingOm de omgeschreven cirkel van een driehoek te tekenen, hebben we genoeg aan 2 middelloodlijnen.
b. Teken de middelloodlijn van KL. Deze is rood in de afbeelding.
c. Teken de middelloodlijn van LM. Deze is groen in de afbeelding.
d. S is het snijpunt van de beide middelloodlijnen. S is blauw in de afbeelding.
e. Zie de paarse cirkel. Zet passerpunt in S en neem straal KS.

12.
a. Zie afbeelding
b. Teken de middelloodlijn van AB en teken de middelloodlijn van BC. Noem het snijpunt van deze 2 middelloodlijnen M. M is het middelpunt van de omgeschreven cirkel. Teken een cirkel met middelpunt M en straal is AM. Je krijgt nu de omgeschreven cirkel.

13.
a. Zie afbeelding
b. Teken de middelloodlijn van AB en teken de middelloodlijn van BC. Noem het snijpunt van deze 2 middelloodlijnen M. M is het middelpunt van de omgeschreven cirkel van driehoek ABC. Teken een cirkel met middelpunt M en straal is AM. Je krijgt nu de omgeschreven cirkel.
c. Want dan had punt O op de omgeschreven cirkel van driehoek ABC moeten liggen. En dat doet O nu dus niet.
d. Zie afbeelding voor punt D. Deze ligt ongeveer op D(-1,5 ; 0).

14.
a. Zie afbeelding
b. Teken eerst een cirkel met middelpunt C en straal is 4. Teken daarna de middelloodlijn van AB. De punten "linksboven" deze middelloodlijn1 liggen dichter bij A dan bij B. Dus teken de cirkelboog rood waar de cirkel linksboven deze middelloodlijn ligt.
c. Teken eerst de middelloodlijn van BC (middelloodlijn2). De gevraagde punten liggen rechts van deze middelloodlijn en binnen de driehoek.

15.
a. Teken een lijnstuk AB. Teken een cirkel met middelpunt A en een straal kleiner dan AB. Teken daarna een cirkel met middelpunt B en dezelfde straal.
Deze 2 cirkels snijden elkaar in 2 punten. Teken een lijn door deze 2 snijpunten. Deze lijn is de middelloodlijn.
b. Je construeert 2 punten met gelijke afstand van zowel A als B. Dus dan liggen deze punten op de middelloodlijn. En je hebt maar 2 punten nodig voor een rechte lijn.
c. Zie afbeelding. Middelpunt omschreven cirkel is snijpunt middelloodlijn 1 en 2.
Deze zit ongeveer op M(-1,25 ; 0,75)

16.
*
Andere paragrafen:
2.1. Cirkel en middelloodlijn (1 t/m 16)
2.2. De bissectrice (17 t/m 28)
2.3. Zwaartelijn en hoogtelijn (29 t/m 39)
2.4. De oppervlakte van een driehoek (40 t/m 49)
2.5. De oppervlakte van een vierhoek (50 t/m 70)
2.1. Cirkel en middelloodlijn (1 t/m 16)
2.2. De bissectrice (17 t/m 28)
2.3. Zwaartelijn en hoogtelijn (29 t/m 39)
2.4. De oppervlakte van een driehoek (40 t/m 49)
2.5. De oppervlakte van een vierhoek (50 t/m 70)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


