TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 2.4 De oppervlakte van een driehoek VWO 2
Boek: Getal & Ruimte - Vlakke figuren VWO 2 (deel 1) opgaven 40 t/m 49, 2009oppervlakte driehoek = 1/2 x zijde x bijbehorende hoogte
Bij een stomphoekige driehoek ligt de hoogte buiten de driehoek.
Bij een stomphoekige driehoek ligt de hoogte buiten de driehoek.
40.
a. opp(ABDE) = 4 x 3 = 12 cm2
b. opp(ABDE) = opp(AFCE)) + opp(FBDC)
Nu links en rechts x 1/2 levert:
1/2 x opp(ABDE) = 1/2 x opp(AFCE)) + 1/2 x opp(FBDC)
1/2 x opp(ABDE) = opp(AFC) + opp(FBC)
1/2 x opp(ABDE) = opp(ABC)
41.
oppervlakte driehoek I = 1/2 x 3 x 2 = 3 cm2
oppervlakte driehoek II = 1/2 x 5 x 1 = 2,5 cm2
oppervlakte driehoek III = 1/2 x 1 x 6 = 3 cm2
oppervlakte driehoek IV = 1/2 x 4 x 2 = 4 cm2
oppervlakte driehoek V = 1/2 x 4 x 2 = 4 cm2
oppervlakte driehoek VI = 1/2 x 1 x 1 = 0,5 cm2
oppervlakte driehoek VII = 1/2 x 4 x 2 = 4 cm2
oppervlakte driehoek VIII = 1/2 x 2 x 3 = 3 cm2
oppervlakte driehoek IX = 1/2 x 5 x 2 = 5 cm2
42.
b. oppervlakte driehoek PQR = 1/2 x zijde x bijbehorende hoogte = 1/2 x 4 x 4 = 8 cm2
c. oppervlakte driehoek OPQ = 1/2 x zijde x bijbehorende hoogte = 1/2 x 4 x 3 = 6 cm2
d. oppervlakte driehoek QRS = 1/2 x zijde x bijbehorende hoogte = 1/2 x 4 x 3 = 6 cm2
43.
Vul in wat je weet:
24 = 1/2 x 6 x h
24 = 3 x h
h = 8
b. oppervlakte driehoek PQR = 1/2 x zijde x bijbehorende hoogte h1 (h1 is nu 7)
Vul in wat je weet:
oppervlakte driehoek PQR = 1/2 x 8 x 7
h = 28
Maar ook geldt:
oppervlakte driehoek PQR = 1/2 x QR x h2 (h2 moet je nu berekenen)
28 = 1/2 x 10 x h2
h2 = 28/5 = 5 3/5
44.
opp = 1/2 x PQ x QR = 1/2 x 20 x 15 = 150
b. QS gaat door Q en staat loodrecht op PR. Noem snijpunt S.
Nu geldt weer: oppervlakte driehoek PQR = 1/2 x zijde x bijbehorende hoogte.
We weten nu dat de opp = 150. Invullen wat je weet, levert:
150 = 1/2 x PR x QS
150 = 1/2 x 25 x QS
QS = 150 / 12,5
QS = 12
45.
a. opp(ABC) = 1/2 x AB x CD = 1/2 x 30 x 16 = 240 mm2
b. Verleng zijde BC. Dus trek de lijn CB door naar linksonder. Teken dan vanuit A de loodlijn op de verlengde BC.
Snijpunt van de hoogtelijn uit A met de verlengde BC is punt E.
c. opp(ABC) = 1/2 x BC x AE, invullen wat je weet:
240 = 1/2 x 20 x AE
240 = 10 x AE
AE = 24 mm
d. opp(ABC) = 1/2 x AC x BF, invullen wat je weet:
240 = 1/2 x 45 x BF
BF = 10 2/3 mm
46.
84 = 1/2 x KL x h
84 = 1/2 x 4 x h
h = 42
Dus de punten die M kan zijn: M(0,42) en M(0,-42).
b. Ook hier maak weer een tekening en kies even een positie voor C om de opgave inzichtelijk te krijgen. Kies even om te proberen: C(-2,0) en teken de driehoek.
Bedenk dat C over de x-as loopt, maar de hoogte (vanuit punt B) is gelijk aan h = 3. Dus nu ligt de hoogte h vast(bekend), maar is de zijde nog onbekend (variabel).
Opp(ABC) = 1/2 x AC x h
36 = 1/2 x AC x 3
36 = 1,5 x AC
AC = 24
Dus als de lengte van zijde AC gelijk is aan 24, krijgen we de coördinaten: C(28,0) of C(-20,0).
c. Kies nu bijvoorbeeld C(0,-4) om de opgave inzichtelijk te krijgen.
Als C over de y-as loopt, is de hoogte OA nu gelijk aan h = 4 (bekend) en de zijde BC onbekend.
Opp(ABC) = 1/2 x BC x h
36 = 1/2 x BC x 4
36 = 2 x BC
BC = 18
Dus als de lengte van zijde BC gelijk is aan 18, krijgen we de coördinaten: C(0,-15) of C(0,21).
47.
oppervlakte driehoek (APB) = 1/2 x 1 x 4 = 2 cm2
oppervlakte driehoek (BQC) = 1/2 x 3 x 1 = 1,5 cm2
Dus opp(GEEL) = 3 + 2 + 1,5 = 6,5 cm2
b. opp(ABC) = opp(rechthoek) - opp(geel)
opp(ABC) = (4 x 3) - 6,5
opp(ABC) = 12 - 6,5 = 5,5 cm2
48.
b.
opp(I) = 1/2 x 3 x 3 = 4,5
opp(II) = 1/2 x 1 x 2 = 1
opp(III) = 1/2 x 4 x 1 = 2
opp(3 driehoeken) = 7,5
opp(ABC) = opp(rechthoek) - opp(3 driehoeken)
opp(ABC) = (4 x 3) - 7,5
opp(ABC) = 12 - 7,5 = 4,5 cm2
c.
opp(OAB) = opp(rechthoek) - opp(3 driehoeken)
opp(OAB) = 16 - 3 - 4 - 2 = 7 cm2
49.
opp(ABC) = 1/2 x 8 x 3 = 12 m2
Dus er moet 2 x 12 = 24 m2 geschilderd worden.
Daar doet de schilder dus 24 / 3 = 8 uur over.
a. opp(ABDE) = 4 x 3 = 12 cm2
b. opp(ABDE) = opp(AFCE)) + opp(FBDC)
Nu links en rechts x 1/2 levert:
1/2 x opp(ABDE) = 1/2 x opp(AFCE)) + 1/2 x opp(FBDC)
1/2 x opp(ABDE) = opp(AFC) + opp(FBC)
1/2 x opp(ABDE) = opp(ABC)
41.
oppervlakte driehoek I = 1/2 x 3 x 2 = 3 cm2
oppervlakte driehoek II = 1/2 x 5 x 1 = 2,5 cm2
oppervlakte driehoek III = 1/2 x 1 x 6 = 3 cm2
oppervlakte driehoek IV = 1/2 x 4 x 2 = 4 cm2
oppervlakte driehoek V = 1/2 x 4 x 2 = 4 cm2
oppervlakte driehoek VI = 1/2 x 1 x 1 = 0,5 cm2
oppervlakte driehoek VII = 1/2 x 4 x 2 = 4 cm2
oppervlakte driehoek VIII = 1/2 x 2 x 3 = 3 cm2
oppervlakte driehoek IX = 1/2 x 5 x 2 = 5 cm2
42.
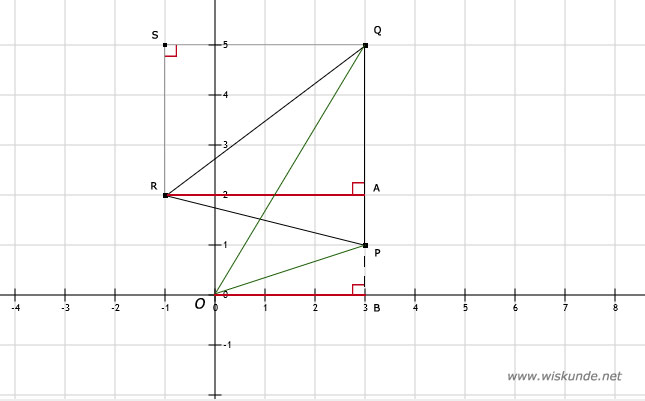
Tip:
De bijbehorende hoogte van driehoek PQR is AR.
De bijbehorende hoogte van driehoek OPQ is OB.
a. Zie afbeeldingDe bijbehorende hoogte van driehoek PQR is AR.
De bijbehorende hoogte van driehoek OPQ is OB.
b. oppervlakte driehoek PQR = 1/2 x zijde x bijbehorende hoogte = 1/2 x 4 x 4 = 8 cm2
c. oppervlakte driehoek OPQ = 1/2 x zijde x bijbehorende hoogte = 1/2 x 4 x 3 = 6 cm2
d. oppervlakte driehoek QRS = 1/2 x zijde x bijbehorende hoogte = 1/2 x 4 x 3 = 6 cm2

43.
Tip:
Maak eerst een schets van de situatie. Dan zie je het beter.
Bedenk: een driehoek heeft 3 zijden, dus ook 3 verschillende bijbehorende hoogtes.
Bijvoorbeeld: h1, h2 en h3
a. oppervlakte driehoek ABC = 1/2 x zijde x bijbehorende hoogteMaak eerst een schets van de situatie. Dan zie je het beter.
Bedenk: een driehoek heeft 3 zijden, dus ook 3 verschillende bijbehorende hoogtes.
Bijvoorbeeld: h1, h2 en h3
Vul in wat je weet:
24 = 1/2 x 6 x h
24 = 3 x h
h = 8
b. oppervlakte driehoek PQR = 1/2 x zijde x bijbehorende hoogte h1 (h1 is nu 7)
Vul in wat je weet:
oppervlakte driehoek PQR = 1/2 x 8 x 7
h = 28
Maar ook geldt:
oppervlakte driehoek PQR = 1/2 x QR x h2 (h2 moet je nu berekenen)
28 = 1/2 x 10 x h2
h2 = 28/5 = 5 3/5
44.
Tip:
Maak eerst een schets van de situatie.
a. oppervlakte driehoek PQR = 1/2 x zijde x bijbehorende hoogteMaak eerst een schets van de situatie.
opp = 1/2 x PQ x QR = 1/2 x 20 x 15 = 150
b. QS gaat door Q en staat loodrecht op PR. Noem snijpunt S.
Nu geldt weer: oppervlakte driehoek PQR = 1/2 x zijde x bijbehorende hoogte.
We weten nu dat de opp = 150. Invullen wat je weet, levert:
150 = 1/2 x PR x QS
150 = 1/2 x 25 x QS
QS = 150 / 12,5
QS = 12
45.
a. opp(ABC) = 1/2 x AB x CD = 1/2 x 30 x 16 = 240 mm2
b. Verleng zijde BC. Dus trek de lijn CB door naar linksonder. Teken dan vanuit A de loodlijn op de verlengde BC.
Snijpunt van de hoogtelijn uit A met de verlengde BC is punt E.
c. opp(ABC) = 1/2 x BC x AE, invullen wat je weet:
240 = 1/2 x 20 x AE
240 = 10 x AE
AE = 24 mm
d. opp(ABC) = 1/2 x AC x BF, invullen wat je weet:
240 = 1/2 x 45 x BF
BF = 10 2/3 mm
46.
Tip:
Bij opgave a: Maak een tekening van de situatie. Kies zelf even een plek voor M om te proberen. Bijvoorbeeld: M(0,3) om zo de situatie te snappen. Je ziet dat driehoek KLM een zijde heeft KL en een bijbehorende hoogte (nog onbekend) van h. Want je weet niet exact waar M ligt.
a. Opp(KLM) = 1/2 x zijde x bijbehorende hoogte, invullen wat je weet:Bij opgave a: Maak een tekening van de situatie. Kies zelf even een plek voor M om te proberen. Bijvoorbeeld: M(0,3) om zo de situatie te snappen. Je ziet dat driehoek KLM een zijde heeft KL en een bijbehorende hoogte (nog onbekend) van h. Want je weet niet exact waar M ligt.
84 = 1/2 x KL x h
84 = 1/2 x 4 x h
h = 42
Dus de punten die M kan zijn: M(0,42) en M(0,-42).
b. Ook hier maak weer een tekening en kies even een positie voor C om de opgave inzichtelijk te krijgen. Kies even om te proberen: C(-2,0) en teken de driehoek.
Bedenk dat C over de x-as loopt, maar de hoogte (vanuit punt B) is gelijk aan h = 3. Dus nu ligt de hoogte h vast(bekend), maar is de zijde nog onbekend (variabel).
Opp(ABC) = 1/2 x AC x h
36 = 1/2 x AC x 3
36 = 1,5 x AC
AC = 24
Dus als de lengte van zijde AC gelijk is aan 24, krijgen we de coördinaten: C(28,0) of C(-20,0).
c. Kies nu bijvoorbeeld C(0,-4) om de opgave inzichtelijk te krijgen.
Als C over de y-as loopt, is de hoogte OA nu gelijk aan h = 4 (bekend) en de zijde BC onbekend.
Opp(ABC) = 1/2 x BC x h
36 = 1/2 x BC x 4
36 = 2 x BC
BC = 18
Dus als de lengte van zijde BC gelijk is aan 18, krijgen we de coördinaten: C(0,-15) of C(0,21).
47.
Tip:
oppervlakte witte driehoek = oppervlakte gehele rechthoek - oppervlakte alle gele driehoeken
a. oppervlakte driehoek (ACR) = 1/2 x 2 x 3 = 3 cm2oppervlakte witte driehoek = oppervlakte gehele rechthoek - oppervlakte alle gele driehoeken
oppervlakte driehoek (APB) = 1/2 x 1 x 4 = 2 cm2
oppervlakte driehoek (BQC) = 1/2 x 3 x 1 = 1,5 cm2
Dus opp(GEEL) = 3 + 2 + 1,5 = 6,5 cm2
b. opp(ABC) = opp(rechthoek) - opp(geel)
opp(ABC) = (4 x 3) - 6,5
opp(ABC) = 12 - 6,5 = 5,5 cm2
48.
Tip:
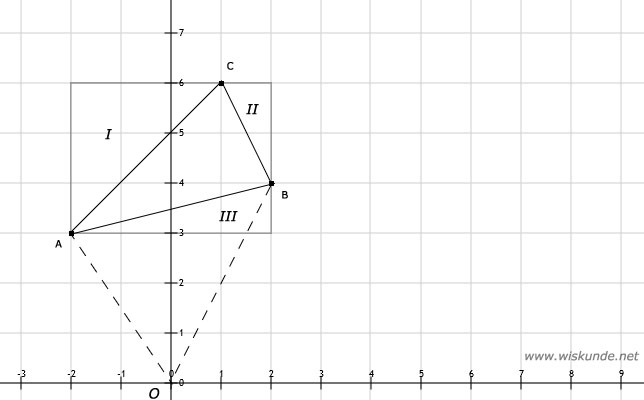
Je kunt nu niet makkelijk de lengte van een zijde of de lengte van de hoogte aflezen.
a. Zie afbeeldingJe kunt nu niet makkelijk de lengte van een zijde of de lengte van de hoogte aflezen.
b.
opp(I) = 1/2 x 3 x 3 = 4,5
opp(II) = 1/2 x 1 x 2 = 1
opp(III) = 1/2 x 4 x 1 = 2
opp(3 driehoeken) = 7,5
opp(ABC) = opp(rechthoek) - opp(3 driehoeken)
opp(ABC) = (4 x 3) - 7,5
opp(ABC) = 12 - 7,5 = 4,5 cm2
c.
opp(OAB) = opp(rechthoek) - opp(3 driehoeken)
opp(OAB) = 16 - 3 - 4 - 2 = 7 cm2

49.
Tip:
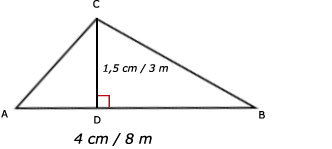
Maak een schets van de driehoek ABC met zijde AB = 4 cm en hoogte CD = 1,5 cm.
Gegeven is schaal 1 : 200. Dat betekent 1 cm in de tekening is 2 m in het echt (200 cm).
Dus 4 cm in het klein, is 8 m in het groot.
Afmetingen van de driehoek in het echt: zijde AB = 8 m en hoogte CD = 3 m.Maak een schets van de driehoek ABC met zijde AB = 4 cm en hoogte CD = 1,5 cm.
Gegeven is schaal 1 : 200. Dat betekent 1 cm in de tekening is 2 m in het echt (200 cm).
Dus 4 cm in het klein, is 8 m in het groot.
opp(ABC) = 1/2 x 8 x 3 = 12 m2
Dus er moet 2 x 12 = 24 m2 geschilderd worden.
Daar doet de schilder dus 24 / 3 = 8 uur over.

Andere paragrafen:
2.1. Cirkel en middelloodlijn (1 t/m 16)
2.2. De bissectrice (17 t/m 28)
2.3. Zwaartelijn en hoogtelijn (29 t/m 39)
2.4. De oppervlakte van een driehoek (40 t/m 49)
2.5. De oppervlakte van een vierhoek (50 t/m 70)
2.1. Cirkel en middelloodlijn (1 t/m 16)
2.2. De bissectrice (17 t/m 28)
2.3. Zwaartelijn en hoogtelijn (29 t/m 39)
2.4. De oppervlakte van een driehoek (40 t/m 49)
2.5. De oppervlakte van een vierhoek (50 t/m 70)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


