TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 6.5 Berekeningen in rechthoekige driehoeken VWO 2
Boek: Getal & Ruimte - De stelling van Pythagoras VWO 2 (deel 2) opgaven 49 t/m 60, 20091. De bach-Stelling:
Het product 'schuine zijde x bijbehorende hoogte' is gelijk aan het product van 'de 2 rechthoekszijden'.
2. De hpq-Stelling:
Als de hoogte h in een rechthoekige driehoek de schuine zijde verdeelt in de stukken p en q dan geldt: h2 = p x q.
3. De Stelling van Thales:
Gegeven een cirkel met daarin een middellijn AB en een punt C op de cirkel, dan is iedere hoek C gelijk aan 90 graden.
Het product 'schuine zijde x bijbehorende hoogte' is gelijk aan het product van 'de 2 rechthoekszijden'.
2. De hpq-Stelling:
Als de hoogte h in een rechthoekige driehoek de schuine zijde verdeelt in de stukken p en q dan geldt: h2 = p x q.
3. De Stelling van Thales:
Gegeven een cirkel met daarin een middellijn AB en een punt C op de cirkel, dan is iedere hoek C gelijk aan 90 graden.
49.
AC2 + BC2 = AB2
32 + 42 = AB2
AB2 = 9 + 16
AB2 = 25
AB = √25
AB = 5
b.
opp1(ABC) = opp2(ABC) (2 manieren)
1/2 x AB x CD = 1/2 x AC x BC
1/2 x 5 x CD = 1/2 x 3 x 4
2,5CD = 6
CD = 2,4
50.
72 + 42 = AC2
AC2 = 49 + 16
AC2 = 65
AC = √65
AC ≈ 8,06
De bach-Stelling:
AB x BC = AC x BE
7 x 4 = √65 x BE
28 = √65 x BE
BE = 28 / √65
BE ≈ 3,5 cm
51.
AC2 + BC2 = AB2
62 + BC2 = 102
BC2 = 100 - 36
BC2 = 64
BC = √64
BC = 8
De bach-Stelling:
AC x BC = AB x CD
6 x 8 = 10 x CD
48 = 10 x CD
CD = 48 / 10
CD = 4,8 cm
b.
KL2 + KM2 = LM2
62 + 62 = LM2
LM2 = 36 + 36
LM2 = 72
LM = √72
LM ≈ 8,49
De bach-Stelling:
KL x KM = LM x KN
6 x 6 = √72 x KN
36 = √72 x KN
KN = 36 / √72
KN ≈ 4,2 cm
52.
202 + 502 = PR2
PR2 = 400 + 2500
PR2 = 2900
PR = √2900
PR ≈ 53,85
De bach-Stelling:
RS x PS = PR x MS
20 x 50 = √2900 x MS
1000 = √2900 x MS
MS = 1000 / √2900
MS ≈ 18,57 cm
Dus QS + PR = (2 x MS) + PR
QS + PR = (2 x 18,57) + √2900
Dus QS + PR = 91,0 cm
Dus de latjes samen zijn 91,0 cm.
53.
a2 + b2 = c2
b.
h2 + p2 = b2
h2 + q2 = a2
--------------- +
2h2 + p2 + q2 = a2 + b2
c.
2h2 + p2 + q2 = c2
d.
c2 = (p+q)2 = (p + q)(p + q) = p2 + 2pq + q2
e.
Uit c. volgt: c2 = 2h2 + p2 + q2
Uit d. volgt: c2 = p2 + 2pq + q2
Stel nu c2 = c2, levert:
2h2 + p2 + q2 = p2 + 2pq + q2
Nu links en rechts wegstrepen: p2 en ook q2
Je houdt dan over:
2h2 = 2pq
Nu links en rechts delen door 2, levert:
h2 = pq
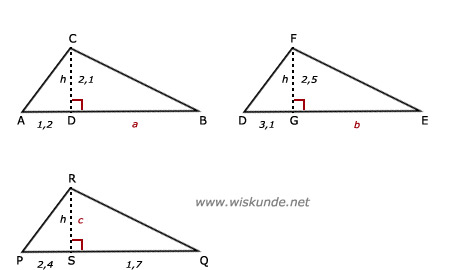
54.
CD2 = AD x BD
2,12 = 1,2 x a
4,41 = 1,2a
a = 4,41 / 1,2
a ≈ 3,7 cm
b.
FG2 = DG x EG
2,52 = 3,1 x b
6,25 = 3,1b
b = 6,25 / 3,1
b ≈ 2,0 cm
c.
RS2 = PS x QS
c2 = 2,4 x 1,7
c2 = 4,08
c = √4,08
c ≈ 2,0 cm
55.
CD2 = AD x BD
3,62 = AD x 2,4
12,96 = AD x 2,4
AD = 12,96 / 2,4
AD = 5,4
Opp(ABC) = 1/2 x basis x hoogte
Opp(ABC) = 1/2 x AB x CD
Opp(ABC) = 1/2 x (AD + BD) x CD
Opp(ABC) = 1/2 x (5,4 + 2,4) x 3,6
Opp(ABC) = 1/2 x 7,8 x 3,6
Opp(ABC) = 14,0 cm2
b.
MN2 = KN x LN
MN2 = 3,7 x 1,4
MN2 = 5,18
MN = √5,18
MN ≈ 2,28
Opp(KLM) = 1/2 x basis x hoogte
Opp(KLM) = 1/2 x KL x MN
Opp(KLM) = 1/2 x (KN + LN) x MN
Opp(KLM) = 1/2 x (3,7 + 1,4) x √5,18
Opp(KLM) = 1/2 x 5,1 x √5,18
Opp(KLM) = 5,8 cm2
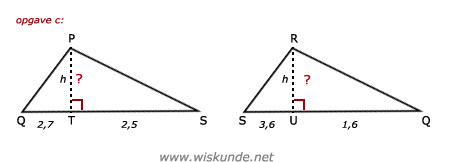
c.
Bereken PT:
PT2 = QT x ST
PT2 = 2,7 x 2,5
PT2 = 6,75
PT = √6,75
PT ≈ 2,60
Opp(PQS) = 1/2 x QS x PT = 1/2 x 5,2 x √6,75 ≈ 6,75 cm2
Bereken RU:
RU2 = SU x QU
RU2 = 3,6 x 1,6
RU2 = 5,76
RU = √5,76
RU = 2,4
Opp(QRS) = 1/2 x QS x RU = 1/2 x 5,2 x 2,4 = 6,24 cm2
Dus opp(totale figuur) = opp(PQRS) = 6,75 + 6,24 = 12,99 cm2
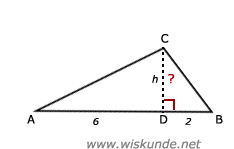
56.
CD2 = AD x BD
CD2 = 6 x 2
CD2 = 12
CD = √12
CD ≈ 3,46 m
Dus hoogte huis: CD + 5 = 3,46 + 5 = 8,46 m.
Dus afgerond is dat 8,5 meter.
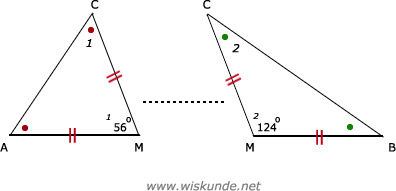
57.
AM = BM = CM omdat het steeds de straal van de cirkel is. De driehoeken zijn dus gelijkbenig.
b.
∠C1 = (180º - 56º) / 2 = 62º
∠C2 = (180º - 124º) / 2 = 28º
∠C12 = ∠C1 + ∠C2 = 62º + 28º = 90º
c.
∠C1 = (180º - 40º) / 2 = 70º
∠C2 = (180º - 140º) / 2 = 20º
∠C12 = ∠C1 + ∠C2 = 70º + 20º = 90º
b.
Hoe groot ∠M1 ook is, altijd is ∠C12 = 90º.
58.
72 + BC2 = 82
BC2 = 64 - 49
BC2 = 15
BC = √15
BC ≈ 3,87
Omtrek driehoek ABC = 8 + √15 + 7 ≈ 18,87 cm
Dat is 189 mm.
Tip:
Driehoek ABC is een bekende 3-4-5 Pythagoras driehoek.
Je kunt de oppervlakte van driehoek ABC op 2 manieren berekenen.
Formule: oppervlakte driehoek = 1/2 x basis x hoogte
a.Driehoek ABC is een bekende 3-4-5 Pythagoras driehoek.
Je kunt de oppervlakte van driehoek ABC op 2 manieren berekenen.
Formule: oppervlakte driehoek = 1/2 x basis x hoogte
AC2 + BC2 = AB2
32 + 42 = AB2
AB2 = 9 + 16
AB2 = 25
AB = √25
AB = 5
b.
opp1(ABC) = opp2(ABC) (2 manieren)
1/2 x AB x CD = 1/2 x AC x BC
1/2 x 5 x CD = 1/2 x 3 x 4
2,5CD = 6
CD = 2,4
50.
Tip:
Bereken eerst AC met de Stelling van Pythagoras.
Bereken daarna BE met de bach-Stelling.
∠ABC is recht want ABCD is een rechthoek.
AB2 + BC2 = AC2Bereken eerst AC met de Stelling van Pythagoras.
Bereken daarna BE met de bach-Stelling.
∠ABC is recht want ABCD is een rechthoek.
72 + 42 = AC2
AC2 = 49 + 16
AC2 = 65
AC = √65
AC ≈ 8,06
De bach-Stelling:
AB x BC = AC x BE
7 x 4 = √65 x BE
28 = √65 x BE
BE = 28 / √65
BE ≈ 3,5 cm
51.
Tip:
De bach-Stelling is eigenlijk niets anders dan dat je op 2 verschillende manieren de oppervlakte van een driehoek uitrekent.
Uiteraard zijn deze 2 oppervlakten aan elkaar gelijk. De 1/2 streep je links en rechts tegen elkaar weg.
Bereken eerst BC en LM met Pythagoras. Gebruik daarna de bach-Stelling.
a.De bach-Stelling is eigenlijk niets anders dan dat je op 2 verschillende manieren de oppervlakte van een driehoek uitrekent.
Uiteraard zijn deze 2 oppervlakten aan elkaar gelijk. De 1/2 streep je links en rechts tegen elkaar weg.
Bereken eerst BC en LM met Pythagoras. Gebruik daarna de bach-Stelling.
AC2 + BC2 = AB2
62 + BC2 = 102
BC2 = 100 - 36
BC2 = 64
BC = √64
BC = 8
De bach-Stelling:
AC x BC = AB x CD
6 x 8 = 10 x CD
48 = 10 x CD
CD = 48 / 10
CD = 4,8 cm
b.
KL2 + KM2 = LM2
62 + 62 = LM2
LM2 = 36 + 36
LM2 = 72
LM = √72
LM ≈ 8,49
De bach-Stelling:
KL x KM = LM x KN
6 x 6 = √72 x KN
36 = √72 x KN
KN = 36 / √72
KN ≈ 4,2 cm
52.
Tip:
Noem M het snijpunt van QS en PR.
PR kan met de Stelling van Pythagoras.
Bereken dan MS met de bach-Stelling.
QS = 2 x MS
RS2 + PS2 = PR2Noem M het snijpunt van QS en PR.
PR kan met de Stelling van Pythagoras.
Bereken dan MS met de bach-Stelling.
QS = 2 x MS
202 + 502 = PR2
PR2 = 400 + 2500
PR2 = 2900
PR = √2900
PR ≈ 53,85
De bach-Stelling:
RS x PS = PR x MS
20 x 50 = √2900 x MS
1000 = √2900 x MS
MS = 1000 / √2900
MS ≈ 18,57 cm
Dus QS + PR = (2 x MS) + PR
QS + PR = (2 x 18,57) + √2900
Dus QS + PR = 91,0 cm
Dus de latjes samen zijn 91,0 cm.
53.
Tip:
Uit deze opgave volgt de hpq-Stelling:
h2 = pq
a. Uit deze opgave volgt de hpq-Stelling:
h2 = pq
a2 + b2 = c2
b.
h2 + p2 = b2
h2 + q2 = a2
--------------- +
2h2 + p2 + q2 = a2 + b2
c.
2h2 + p2 + q2 = c2
d.
c2 = (p+q)2 = (p + q)(p + q) = p2 + 2pq + q2
e.
Uit c. volgt: c2 = 2h2 + p2 + q2
Uit d. volgt: c2 = p2 + 2pq + q2
Stel nu c2 = c2, levert:
2h2 + p2 + q2 = p2 + 2pq + q2
Nu links en rechts wegstrepen: p2 en ook q2
Je houdt dan over:
2h2 = 2pq
Nu links en rechts delen door 2, levert:
h2 = pq
54.
Tip:
Geef hoekpunten aan de driehoeken en schrijf de hpq-stelling steeds goed op.
Vul in wat je weet. Bereken zo a, b en c.
Kijk goed naar de afbeeldingen.
a.Geef hoekpunten aan de driehoeken en schrijf de hpq-stelling steeds goed op.
Vul in wat je weet. Bereken zo a, b en c.
Kijk goed naar de afbeeldingen.
CD2 = AD x BD
2,12 = 1,2 x a
4,41 = 1,2a
a = 4,41 / 1,2
a ≈ 3,7 cm
b.
FG2 = DG x EG
2,52 = 3,1 x b
6,25 = 3,1b
b = 6,25 / 3,1
b ≈ 2,0 cm
c.
RS2 = PS x QS
c2 = 2,4 x 1,7
c2 = 4,08
c = √4,08
c ≈ 2,0 cm

55.
Tip:
Zorg ervoor dat je de h, p en q weet om de hpq-stelling te gebruiken.
Bij c: Splits in 2 driehoeken: driehoek PQS en driehoek QRS.
Gebruik in beide driehoeken de hpq-stelling.
Bereken zo dus PT en RU. Dit zijn de hoogten in de 2 driehoeken.
Oppervlakte driehoek = 1/2 x basis x bijbehorende hoogte
a.Zorg ervoor dat je de h, p en q weet om de hpq-stelling te gebruiken.
Bij c: Splits in 2 driehoeken: driehoek PQS en driehoek QRS.
Gebruik in beide driehoeken de hpq-stelling.
Bereken zo dus PT en RU. Dit zijn de hoogten in de 2 driehoeken.
Oppervlakte driehoek = 1/2 x basis x bijbehorende hoogte
CD2 = AD x BD
3,62 = AD x 2,4
12,96 = AD x 2,4
AD = 12,96 / 2,4
AD = 5,4
Opp(ABC) = 1/2 x basis x hoogte
Opp(ABC) = 1/2 x AB x CD
Opp(ABC) = 1/2 x (AD + BD) x CD
Opp(ABC) = 1/2 x (5,4 + 2,4) x 3,6
Opp(ABC) = 1/2 x 7,8 x 3,6
Opp(ABC) = 14,0 cm2
b.
MN2 = KN x LN
MN2 = 3,7 x 1,4
MN2 = 5,18
MN = √5,18
MN ≈ 2,28
Opp(KLM) = 1/2 x basis x hoogte
Opp(KLM) = 1/2 x KL x MN
Opp(KLM) = 1/2 x (KN + LN) x MN
Opp(KLM) = 1/2 x (3,7 + 1,4) x √5,18
Opp(KLM) = 1/2 x 5,1 x √5,18
Opp(KLM) = 5,8 cm2
c.
Bereken PT:
PT2 = QT x ST
PT2 = 2,7 x 2,5
PT2 = 6,75
PT = √6,75
PT ≈ 2,60
Opp(PQS) = 1/2 x QS x PT = 1/2 x 5,2 x √6,75 ≈ 6,75 cm2
Bereken RU:
RU2 = SU x QU
RU2 = 3,6 x 1,6
RU2 = 5,76
RU = √5,76
RU = 2,4
Opp(QRS) = 1/2 x QS x RU = 1/2 x 5,2 x 2,4 = 6,24 cm2
Dus opp(totale figuur) = opp(PQRS) = 6,75 + 6,24 = 12,99 cm2

56.
Tip:
Maak een schets van driehoek ABC en gebruik de hpq-stelling.
Bereken dus CD, want hoogte huis is CD + 5.
hpq-Stelling:Maak een schets van driehoek ABC en gebruik de hpq-stelling.
Bereken dus CD, want hoogte huis is CD + 5.
CD2 = AD x BD
CD2 = 6 x 2
CD2 = 12
CD = √12
CD ≈ 3,46 m
Dus hoogte huis: CD + 5 = 3,46 + 5 = 8,46 m.
Dus afgerond is dat 8,5 meter.

57.
Tip:
Zie afbeelding. We snijden driehoek ABC even in 2 stukken.
In een gelijkbenige driehoek zijn de basishoeken even groot.
Gebruik: ∠M1 + ∠M2 = 180º
a.Zie afbeelding. We snijden driehoek ABC even in 2 stukken.
In een gelijkbenige driehoek zijn de basishoeken even groot.
Gebruik: ∠M1 + ∠M2 = 180º
AM = BM = CM omdat het steeds de straal van de cirkel is. De driehoeken zijn dus gelijkbenig.
b.
∠C1 = (180º - 56º) / 2 = 62º
∠C2 = (180º - 124º) / 2 = 28º
∠C12 = ∠C1 + ∠C2 = 62º + 28º = 90º
c.
∠C1 = (180º - 40º) / 2 = 70º
∠C2 = (180º - 140º) / 2 = 20º
∠C12 = ∠C1 + ∠C2 = 70º + 20º = 90º
b.
Hoe groot ∠M1 ook is, altijd is ∠C12 = 90º.

58.
Tip:
Uit de Stelling van Thales volgt: ∠ACB = 90º
Dus bereken BC met de Stelling van Pythagoras.
Omtrek driehoek ABC is: AB + BC + AC
AC2 + BC2 = AB2Uit de Stelling van Thales volgt: ∠ACB = 90º
Dus bereken BC met de Stelling van Pythagoras.
Omtrek driehoek ABC is: AB + BC + AC
72 + BC2 = 82
BC2 = 64 - 49
BC2 = 15
BC = √15
BC ≈ 3,87
Omtrek driehoek ABC = 8 + √15 + 7 ≈ 18,87 cm
Dat is 189 mm.
59.
Oppervlakte vierhoek PQRS is 15,80 cm2
60.
Oppervlakte rode gebied is 22,20 cm2
Oppervlakte vierhoek PQRS is 15,80 cm2
60.
Oppervlakte rode gebied is 22,20 cm2
Andere paragrafen:
6.1. Rechthoekige driehoeken (1 t/m 9)
6.2. Het berekenen van schuine zijden (10 t/m 21)
6.3. Berekeningen met de stelling van Pythagoras (22 t/m 37)
6.4. Pythagoras in de ruimte (38 t/m 48)
6.5. Berekeningen in rechthoekige driehoeken (49 t/m 60)
6.6. Gemengde opgaven (61 t/m 66)
6.1. Rechthoekige driehoeken (1 t/m 9)
6.2. Het berekenen van schuine zijden (10 t/m 21)
6.3. Berekeningen met de stelling van Pythagoras (22 t/m 37)
6.4. Pythagoras in de ruimte (38 t/m 48)
6.5. Berekeningen in rechthoekige driehoeken (49 t/m 60)
6.6. Gemengde opgaven (61 t/m 66)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


