TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 6.2 Het berekenen van schuine zijden VWO 2
Boek: Getal & Ruimte - De stelling van Pythagoras VWO 2 (deel 2) opgaven 10 t/m 21, 2009Als de 2 rechthoekszijden zijn gegeven in een rechthoekige driehoek dan kun je de schuine zijde berekenen met de Stelling van Pythagoras.
Maak indien nodig een schets van de situatie om meer inzicht te krijgen.
De schuine zijde noemen we ook wel de hypotenusa.
Als laatste stap nemen we altijd de wortel.
Maak indien nodig een schets van de situatie om meer inzicht te krijgen.
De schuine zijde noemen we ook wel de hypotenusa.
Als laatste stap nemen we altijd de wortel.
10.
b. 42 + 32 = BC2
Dus BC2 = 16 + 9 = 25
c. BC = √25 = 5 cm
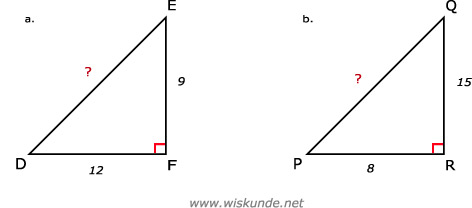
11.
DF2 + EF2 = DE2
122 + 92 = DE2
DE2 = 144 + 81
DE2 = 225
DE = √225
DE = 15
b.
PR2 + QR2 = PQ2
82 + 152 = PQ2
PQ2 = 64 + 225
PQ2 = 289
PQ = √289
PQ = 17
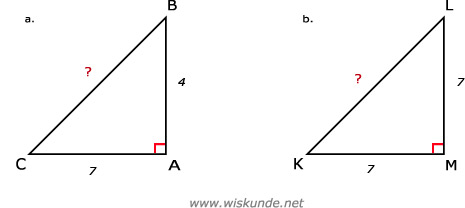
12.
AC2 + AB2 = BC2
72 + 42 = BC2
BC2 = 49 + 16
BC2 = 65
BC = √65
BC ≈ 8,1
b.
KM2 + LM2 = KL2
72 + 72 = KL2
KL2 = 49 + 49
KL2 = 98
KL = √98
KL ≈ 9,9
13.
KM2 + LM2 = KL2
1,72 + 3,52 = KL2
KL2 = 15,14
KL = √15,14
KL ≈ 3,9
b.
AB2 + AC2 = BC2
3,72 + 1,92 = BC2
BC2 = 17,3
BC = √17,3
BC ≈ 4,2
14.
1,42 + 1,92 = AC2
AC2 = 5,57
AC = √5,57
AC ≈ 2,4
BD2 + CD2 = BC2
2,42 + 1,92 = BC2
BC2 = 9,37
BC = √9,37
BC ≈ 3,1
Omtrek driehoek ABC = AD + BD + BC + AC = 1,4 + 2,4 + 3,1 + 2,4 = 9,3
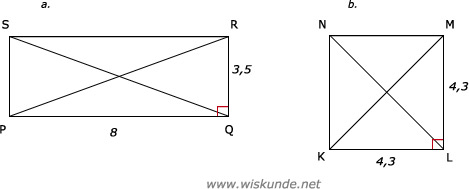
15.
PQ2 + QR2 = PR2
82 + 3,52 = PR2
PR2 = 76,25
PR = √76,25
PR ≈ 8,73
Dus de 2 diagonalen in de rechthoek zijn 8,73 cm lang.
b.
KL2 + LM2 = KM2
4,32 + 4,32 = KM2
KM2 = 36,98
KM = √36,98
KM ≈ 6,08
Dus de 2 diagonalen in het vierkant zijn 6,08 cm lang.
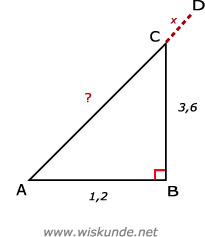
16.
1,22 + 3,62 = AC2
AC2 = 14,4
AC = √14,4
AC ≈ 3,79 meter.
Dus CD = 4,5 - AC = 4,5 - 3,79 = 0,71 meter.
Dus de ladder steekt 71 cm boven de schutting uit.
17.
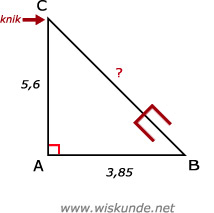
3,852 + 5,62 = BC2
BC2 = 46,1825
BC = √46,1825
BC ≈ 6,80 meter.
Hoogte mast = AC + BC = 5,6 + 6,80 = 12,4 meter.
18.
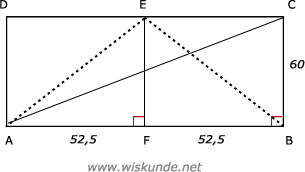
AB2 + BC2 = AC2
1052 + 602 = AC2
AC2 = 14625
AC = √14625
AC ≈ 120,93 meter.
AB + BC + AC = 105 + 60 + 120,93 = 285,93 meter.
b.
AF2 + EF2 = AE2
52,52 + 602 = AE2
AE2 = 6356,25
AE = √6356,25
AE ≈ 79,73 meter.
AB + BE + AE = 105 + 79,73 + 79,73 = 264,46 meter.
19.
2252 + 3502 = CD2
CD2 = 173125
CD = √173125
CD ≈ 416,08 meter.
Dus de lengte van de kabel is 416,1 meter.
Tip:
De 3-4-5 driehoek is een bijzondere Pythagoras-driehoek. Er zijn er meer. Zo ook de 5-12-13.
a. AB2 + AC2 = BC2 De 3-4-5 driehoek is een bijzondere Pythagoras-driehoek. Er zijn er meer. Zo ook de 5-12-13.
b. 42 + 32 = BC2
Dus BC2 = 16 + 9 = 25
c. BC = √25 = 5 cm
11.
Tip:
Maak een schets en schrijf daarna de Stelling van Pythagoras op. Vul daarna in wat je weet.
In deze opgave komen de wortels mooi uit. Dat is niet altijd zo.
a.Maak een schets en schrijf daarna de Stelling van Pythagoras op. Vul daarna in wat je weet.
In deze opgave komen de wortels mooi uit. Dat is niet altijd zo.
DF2 + EF2 = DE2
122 + 92 = DE2
DE2 = 144 + 81
DE2 = 225
DE = √225
DE = 15
b.
PR2 + QR2 = PQ2
82 + 152 = PQ2
PQ2 = 64 + 225
PQ2 = 289
PQ = √289
PQ = 17

12.
Tip:
Maak een schets en schrijf daarna de Stelling van Pythagoras op. Vul daarna in wat je weet.
In deze opgave hebben we geen mooie wortels. Rond dan netjes af. En gebruik het ≈ -teken.
a.Maak een schets en schrijf daarna de Stelling van Pythagoras op. Vul daarna in wat je weet.
In deze opgave hebben we geen mooie wortels. Rond dan netjes af. En gebruik het ≈ -teken.
AC2 + AB2 = BC2
72 + 42 = BC2
BC2 = 49 + 16
BC2 = 65
BC = √65
BC ≈ 8,1
b.
KM2 + LM2 = KL2
72 + 72 = KL2
KL2 = 49 + 49
KL2 = 98
KL = √98
KL ≈ 9,9

13.
Tip:
Bij opgave b. zie je dat BC horizontaal ligt.
Bedenk wel dat BC de schuine zijde is van driehoek ABC.
a.Bij opgave b. zie je dat BC horizontaal ligt.
Bedenk wel dat BC de schuine zijde is van driehoek ABC.
KM2 + LM2 = KL2
1,72 + 3,52 = KL2
KL2 = 15,14
KL = √15,14
KL ≈ 3,9
b.
AB2 + AC2 = BC2
3,72 + 1,92 = BC2
BC2 = 17,3
BC = √17,3
BC ≈ 4,2
14.
Tip:
Bereken eerst AC en BC met de Stelling van Pythagoras.
Tel dan alle zijden op voor de omtrek.
De omtrek is: AD + BD + BC + AC
AD2 + CD2 = AC2Bereken eerst AC en BC met de Stelling van Pythagoras.
Tel dan alle zijden op voor de omtrek.
De omtrek is: AD + BD + BC + AC
1,42 + 1,92 = AC2
AC2 = 5,57
AC = √5,57
AC ≈ 2,4
BD2 + CD2 = BC2
2,42 + 1,92 = BC2
BC2 = 9,37
BC = √9,37
BC ≈ 3,1
Omtrek driehoek ABC = AD + BD + BC + AC = 1,4 + 2,4 + 3,1 + 2,4 = 9,3
15.
Tip:
Maak bij beide opgaven een schets.
De diagonalen van een rechthoek en een vierkant zijn even lang.
a.Maak bij beide opgaven een schets.
De diagonalen van een rechthoek en een vierkant zijn even lang.
PQ2 + QR2 = PR2
82 + 3,52 = PR2
PR2 = 76,25
PR = √76,25
PR ≈ 8,73
Dus de 2 diagonalen in de rechthoek zijn 8,73 cm lang.
b.
KL2 + LM2 = KM2
4,32 + 4,32 = KM2
KM2 = 36,98
KM = √36,98
KM ≈ 6,08
Dus de 2 diagonalen in het vierkant zijn 6,08 cm lang.

16.
Tip:
Bereken eerst AC. Deze is natuurlijk korter dan de ladder (AD = 4,5). Bereken dan 4,5 - AC.
Dat is de lengte (CD = x) dat de ladder boven de schutting uitsteekt.
AB2 + BC2 = AC2Bereken eerst AC. Deze is natuurlijk korter dan de ladder (AD = 4,5). Bereken dan 4,5 - AC.
Dat is de lengte (CD = x) dat de ladder boven de schutting uitsteekt.
1,22 + 3,62 = AC2
AC2 = 14,4
AC = √14,4
AC ≈ 3,79 meter.
Dus CD = 4,5 - AC = 4,5 - 3,79 = 0,71 meter.
Dus de ladder steekt 71 cm boven de schutting uit.

17.
Tip:
Maak een Pythagoras driehoek ABC.
Hoogte mast = AC + BC.
AB2 + AC2 = BC2Maak een Pythagoras driehoek ABC.
Hoogte mast = AC + BC.
3,852 + 5,62 = BC2
BC2 = 46,1825
BC = √46,1825
BC ≈ 6,80 meter.
Hoogte mast = AC + BC = 5,6 + 6,80 = 12,4 meter.

18.
Tip:
Bij a. bereken eerst met Pythagoras de afstand AC in driehoek ABC.
Bij b. bereken met Pythagoras de afstand AE in driehoek AFE. Je weet dat AE = BE.
a.Bij a. bereken eerst met Pythagoras de afstand AC in driehoek ABC.
Bij b. bereken met Pythagoras de afstand AE in driehoek AFE. Je weet dat AE = BE.
AB2 + BC2 = AC2
1052 + 602 = AC2
AC2 = 14625
AC = √14625
AC ≈ 120,93 meter.
AB + BC + AC = 105 + 60 + 120,93 = 285,93 meter.
b.
AF2 + EF2 = AE2
52,52 + 602 = AE2
AE2 = 6356,25
AE = √6356,25
AE ≈ 79,73 meter.
AB + BE + AE = 105 + 79,73 + 79,73 = 264,46 meter.

19.
Tip:
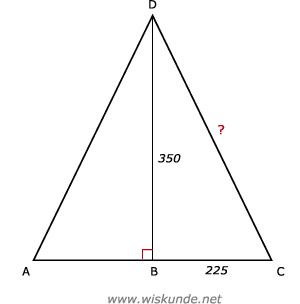
BD = 365 - 15 = 350
CD is de lengte van de kabel.
BC2 + BD2 = CD2BD = 365 - 15 = 350
CD is de lengte van de kabel.
2252 + 3502 = CD2
CD2 = 173125
CD = √173125
CD ≈ 416,08 meter.
Dus de lengte van de kabel is 416,1 meter.

20.
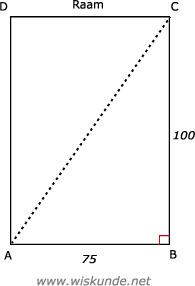
752 + 1002 = AC2
AC2 = 15625
AC = √15625
AC = 125 cm
Dus als je het blad juist draait, dan kan het blad van 122 cm er doorheen.
21.
AB = omtrek cirkel = π x diameter
AB = π x 9
AB ≈ 28,3 cm
AB2 + BC2 = AC2
28,32 + 212 = AC2
AC2 = 1241,89
AC = √1241,89
AC ≈ 35,24 cm
Dus de lengte van het rode touwtje is 352 mm.
Tip:
Bereken de lengte van AC. Dat is de maximale lengte wat het blad kan hebben om door het raam te kunnen.
AB2 + BC2 = AC2Bereken de lengte van AC. Dat is de maximale lengte wat het blad kan hebben om door het raam te kunnen.
752 + 1002 = AC2
AC2 = 15625
AC = √15625
AC = 125 cm
Dus als je het blad juist draait, dan kan het blad van 122 cm er doorheen.

21.
Tip:
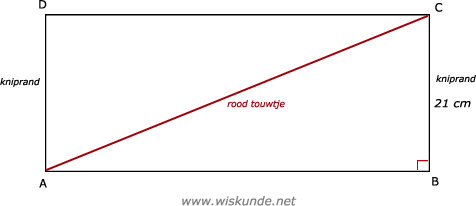
Knip de cilinder door en rol deze uit. Je krijgt dan een rechthoek.
AB (in mijn schets!) is de omtrek van de "grond" cirkel.
Omtrek cirkel = π x diameter
AC is het rode touwtje.
Je krijgt nu dus een Pythagoras driehoek ABC.
Bereken eerst AB.Knip de cilinder door en rol deze uit. Je krijgt dan een rechthoek.
AB (in mijn schets!) is de omtrek van de "grond" cirkel.
Omtrek cirkel = π x diameter
AC is het rode touwtje.
Je krijgt nu dus een Pythagoras driehoek ABC.
AB = omtrek cirkel = π x diameter
AB = π x 9
AB ≈ 28,3 cm
AB2 + BC2 = AC2
28,32 + 212 = AC2
AC2 = 1241,89
AC = √1241,89
AC ≈ 35,24 cm
Dus de lengte van het rode touwtje is 352 mm.

Andere paragrafen:
6.1. Rechthoekige driehoeken (1 t/m 9)
6.2. Het berekenen van schuine zijden (10 t/m 21)
6.3. Berekeningen met de stelling van Pythagoras (22 t/m 37)
6.4. Pythagoras in de ruimte (38 t/m 48)
6.5. Berekeningen in rechthoekige driehoeken (49 t/m 60)
6.6. Gemengde opgaven (61 t/m 66)
6.1. Rechthoekige driehoeken (1 t/m 9)
6.2. Het berekenen van schuine zijden (10 t/m 21)
6.3. Berekeningen met de stelling van Pythagoras (22 t/m 37)
6.4. Pythagoras in de ruimte (38 t/m 48)
6.5. Berekeningen in rechthoekige driehoeken (49 t/m 60)
6.6. Gemengde opgaven (61 t/m 66)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


