TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 6.4 Pythagoras in de ruimte VWO 2
Boek: Getal & Ruimte - De stelling van Pythagoras VWO 2 (deel 2) opgaven 38 t/m 48, 2009De grensvlakken van een balk zijn rechthoeken.
Een diagonaalvlak is een vlak dat gaat door de lichaamsdiagonaal van een balk of kubus.
Een balk heeft 6 diagonaalvlakken. De hoeken in een diagonaalvlak zijn recht.
Om de lengte van een lichaamsdiagonaal in een balk of kubus te berekenen, gebruik je de Stelling van Pythagoras 2 keer achter elkaar. Kijk eerst goed in welk diagonaalvlak de lichaamsdiagonaal ligt.
Een diagonaalvlak is een vlak dat gaat door de lichaamsdiagonaal van een balk of kubus.
Een balk heeft 6 diagonaalvlakken. De hoeken in een diagonaalvlak zijn recht.
Om de lengte van een lichaamsdiagonaal in een balk of kubus te berekenen, gebruik je de Stelling van Pythagoras 2 keer achter elkaar. Kijk eerst goed in welk diagonaalvlak de lichaamsdiagonaal ligt.
38.
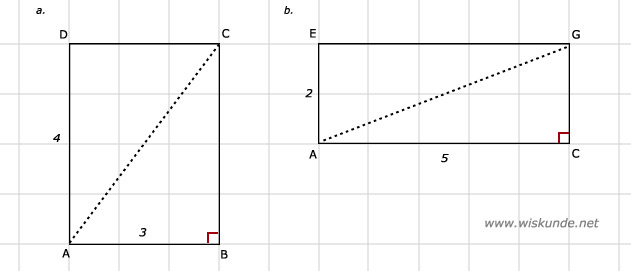
AB2 + BC2 = AC2
32 + 42 = AC2
AC2 = 9 + 16
AC2 = 25
AC = √25
AC = 5 cm
b.
Vierhoek ACGE is een rechthoek. De zijden zijn: 5 x 2 cm.
c.
AC2 + CG2 = AG2
52 + 22 = AG2
AG2 = 25 + 4
AG2 = 29
AG = √29
AG ≈ 5,39 cm
39.
AB2 + AD2 = BD2
52 + 32 = BD2
BD2 = 25 + 9
BD2 = 34
BD = √34
BD ≈ 5,83
BD2 + DH2 = BH2
34 + 32 = BH2
BH2 = 34 + 9
BH2 = 43
BH = √43
BH ≈ 6,6 cm
b.
Alle lichaamsdiagonalen in een balk of kubus zijn even lang.
40.
41.
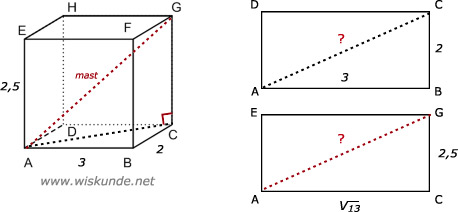
32 + 22 = AC2
AC2 = 9 + 4
AC2 = 13
AC = √13
AC ≈ 3,6 m
AC2 + CG2 = AG2
13 + 2,52 = AG2
AG2 = 19,25
AG = √19,25
AG ≈ 4,39 m
Dus de maximale lengte van de mast (AG) die in het huisje past, is 4,39 meter.
De werkelijke mast is echter 4,5 meter.
Dus je moet er: 4,5 m - 4,39 m = 0,11 meter van afzagen. Dat is 11 cm.
42.
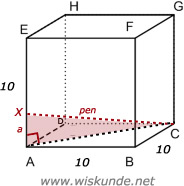
102 + 102 = AC2
AC2 = 100 + 100
AC2 = 200
AC = √200
AC ≈ 14,14
Bereken nu AX (=a) in driehoek ACX:
AC2 + AX2 = CX2
200 + AX2 = 16,52
AX2 = 16,52 - 200
AX2 = 72,25
AX = √72,25
AX = 8,5 cm
Dus de hoogte van a is 8,5 cm.
43.
Hoogte huis is: 4,95 m + 3 m = 7,95 meter
Totale oppervlakte = 2 x (26,18 + 21,86) = 96,08 m2
44.
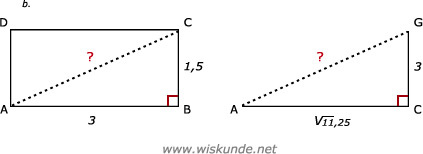
Oppervlakte totale glas = opp(ABFE) + opp(EFGH) + 2 x opp(FPG) + 2 x opp(BCPF)
opp(ABFE) = AB x BF = 3 x 1 = 3
opp(EFGH) = EF x FG = 3 x 2,5 = 7,5
opp(FPG) = 1/2 x basis x hoogte = 1/2 x FP x GP = 1/2 x 1,5 x 2 = 1,5
opp(BCPF) = BC x PC = 1,5 x 1 = 1,5
De totale oppervlakte = 3 + 7,5 + (2 x 1,5) + (2 x 1,5) = 3 + 7,5 + 3 + 3 = 16,5 m2
b.
Zie afbeelding:
AB2 + BC2 = AC2
32 + 1,52 = AC2
AC2 = 11,25
AC = √11,25
AC ≈ 3,35 meter
AC2 + CG2 = AG2
11,25 + 32 = AG2
AG2 = 20,25
AG = √20,25
AG = 4,5 meter
Aantal meter stang dat nodig is: 2 x AG = 2 x 4,5 = 9 meter.
45.
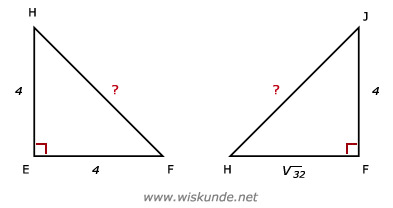
Bereken eerst FH in driehoek EFH.
EF2 + EH2 = FH2
42 + 42 = FH2
FH2 = 32
FH = √32
FH ≈ 5,66 cm
FH2 + FJ2 = HJ2
32 + 42 = HJ2
HJ2 = 48
HJ = √48
HJ ≈ 6,93 cm
Dus BH = HJ = √48 ≈ 6,93 cm.
b.
Als ∠BHJ rechthoekig is, dan moet gelden:
BH2 + HJ2 = BJ2 (is dat wel zo?)
48 + 48 =(?) 82
96 =(?) 64
Nee, je ziet dat de Stelling van Pythagoras niet geldt. Dus ∠BHJ is niet rechthoekig.
46.
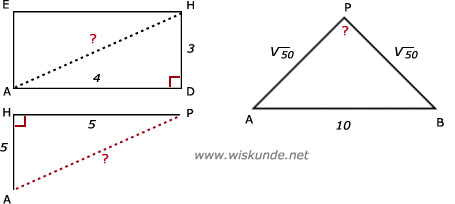
AD2 + DH2 = AH2
42 + 32 = AH2
AH2 = 25
AH = √25
AH = 5
Bereken dan AP in driehoek AHP.
AH2 + HP2 = AP2
52 + 52 = AP2
AP2 = 50
AP = √50
AP ≈ 7,07
We hebben nu een "mogelijke" Pythagoras driehoek ABP.
Dan moet dus gelden:
AP2 + BP2 = AB2 (Is dat wel zo?)
(√50)2 + (√50)2 = 102 (?)
50 + 50 = 100 (?)
100 = 100
Ja, dat klopt zeker! Dus dan moet de hoek wel 90º zijn.
Dus driehoek ABP is rechthoekig.
47.
EF2 = 122 + 32
EF2 = 144 + 9
EF2 = 153
EF = √153
EF ≈ 12,37 m
FG2 = 122 + 12
FG2 = 144 + 1
FG2 = 145
FG = √145
FG ≈ 12,04 m
GH2 = 122 + 32
GH2 = 144 + 9
GH2 = 153
GH = √153
GH ≈ 12,37 m
EH2 = 122 + 12
EH2 = 144 + 1
EH2 = 145
EH = √145
EH ≈ 12,04 m
Dus omtrek EFGH = √153 + √145 + √153 + √145 = 48,82 meter. Dat is dus 488 dm.
b.
AC2 = AB2 + BC2
AC2 = 122 + 122
AC2 = 144 + 144
AC2 = 288
AC = √288
AC ≈ 16,97 m
Nu de vraag of geldt: EF2 + FG2 = EG2 (?)
(√153)2 + (√145)2 = (√292)2 (?)
153 + 145 = 292 (?)
298 = 292 (?)
Nee, dat klopt niet. Dus ∠EFG is niet recht. Dus kan EFGH nooit een rechthoek zijn.
Tip:
AG is een lichaamsdiagonaal.
Een diagonaalvlak is een rechthoek.
a. AG is een lichaamsdiagonaal.
Een diagonaalvlak is een rechthoek.
AB2 + BC2 = AC2
32 + 42 = AC2
AC2 = 9 + 16
AC2 = 25
AC = √25
AC = 5 cm
b.
Vierhoek ACGE is een rechthoek. De zijden zijn: 5 x 2 cm.
c.
AC2 + CG2 = AG2
52 + 22 = AG2
AG2 = 25 + 4
AG2 = 29
AG = √29
AG ≈ 5,39 cm

39.
Tip:
Bereken eerst BD met Pythagoras in driehoek BAD. Bedenk: ∠BAD = 90º
Bereken daarna BH met Pythagoras in driehoek BDH. Bedenk: ∠BDH = 90º
a. Bereken eerst BD met Pythagoras in driehoek BAD. Bedenk: ∠BAD = 90º
Bereken daarna BH met Pythagoras in driehoek BDH. Bedenk: ∠BDH = 90º
AB2 + AD2 = BD2
52 + 32 = BD2
BD2 = 25 + 9
BD2 = 34
BD = √34
BD ≈ 5,83
BD2 + DH2 = BH2
34 + 32 = BH2
BH2 = 34 + 9
BH2 = 43
BH = √43
BH ≈ 6,6 cm
b.
Alle lichaamsdiagonalen in een balk of kubus zijn even lang.
40.
Tip:
Bij a:
Bereken eerst met de Stelling van Pythagoras BD in driehoek BAD. Bedenk: ∠BAD = 90º
Bereken dan met de Stelling van Pythagoras DF in driehoek FBD. Bedenk: ∠FBD = 90º
Bij b:
Bereken eerst met de Stelling van Pythagoras AH in driehoek ADH. Bedenk: ∠ADH = 90º
Bereken dan met de Stelling van Pythagoras AP in driehoek PHA. Bedenk: ∠PHA = 90º
Bij a:
Bereken eerst met de Stelling van Pythagoras BD in driehoek BAD. Bedenk: ∠BAD = 90º
Bereken dan met de Stelling van Pythagoras DF in driehoek FBD. Bedenk: ∠FBD = 90º
Bij b:
Bereken eerst met de Stelling van Pythagoras AH in driehoek ADH. Bedenk: ∠ADH = 90º
Bereken dan met de Stelling van Pythagoras AP in driehoek PHA. Bedenk: ∠PHA = 90º
|
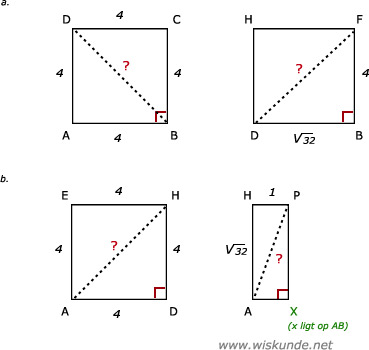
a. AB2 + AD2 = BD2 42 + 42 = BD2 BD2 = 16 + 16 BD2 = 32 BD = √32 BD ≈ 5,66 cm BD2 + BF2 = DF2 32 + 42 = DF2 DF2 = 32 + 16 DF2 = 48 DF = √48 DF ≈ 6,9 cm |
b. AD2 + DH2 = AH2 42 + 42 = AH2 AH2 = 16 + 16 AH2 = 32 AH = √32 AH ≈ 5,66 cm AH2 + HP2 = AP2 32 + 12 = AP2 AP2 = 32 + 1 AP2 = 33 AP = √33 AP ≈ 5,7 cm |

41.
Tip:
De maximale lengte van de mast is de lengte van de lichaamsdiagonaal AG.
Bereken eerst AC.
Bereken dan AG.
AB2 + BC2 = AC2De maximale lengte van de mast is de lengte van de lichaamsdiagonaal AG.
Bereken eerst AC.
Bereken dan AG.
32 + 22 = AC2
AC2 = 9 + 4
AC2 = 13
AC = √13
AC ≈ 3,6 m
AC2 + CG2 = AG2
13 + 2,52 = AG2
AG2 = 19,25
AG = √19,25
AG ≈ 4,39 m
Dus de maximale lengte van de mast (AG) die in het huisje past, is 4,39 meter.
De werkelijke mast is echter 4,5 meter.
Dus je moet er: 4,5 m - 4,39 m = 0,11 meter van afzagen. Dat is 11 cm.

42.
Tip:
Bereken eerst AC. Bereken dan AX in de rechthoekige driehoek ACX.
Als je AX weet, dan weet je ook de lengte van a.
CX is de pen. Ik heb de kubus in mijn schets een beetje gedraaid.
AB2 + BC2 = AC2Bereken eerst AC. Bereken dan AX in de rechthoekige driehoek ACX.
Als je AX weet, dan weet je ook de lengte van a.
CX is de pen. Ik heb de kubus in mijn schets een beetje gedraaid.
102 + 102 = AC2
AC2 = 100 + 100
AC2 = 200
AC = √200
AC ≈ 14,14
Bereken nu AX (=a) in driehoek ACX:
AC2 + AX2 = CX2
200 + AX2 = 16,52
AX2 = 16,52 - 200
AX2 = 72,25
AX = √72,25
AX = 8,5 cm
Dus de hoogte van a is 8,5 cm.

43.
Tip:
Bij a: Bereken eerst EG met de Stelling van Pythagoras.
Bij b: Bereken daarna TS.
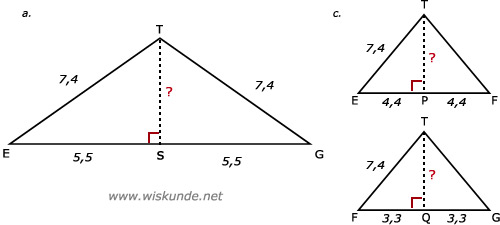
Bij c: Bereken de hoogten in de driehoeken EFT en FGT.
Bepaal dan de oppervlakte van elke driehoek. Vermenigvuldig dan maal 2.
Bij a: Bereken eerst EG met de Stelling van Pythagoras.
Bij b: Bereken daarna TS.
Bij c: Bereken de hoogten in de driehoeken EFT en FGT.
Bepaal dan de oppervlakte van elke driehoek. Vermenigvuldig dan maal 2.
|
a. Zie afbeelding EF2 + FG2 = EG2 8,82 + 6,62 = EG2 EG2 = 121 EG = √121 EG = 11 meter |
b. ST2 + GS2 = GT2 ST2 + 5,52 = 7,42 ST2 = 7,42 - 5,52 ST2 = 24,51 ST = √24,51 ST ≈ 4,95 meter |
|
c. EP2 + PT2 = ET2 4,42 + PT2 = 7,42 PT2 = 35,4 PT = √35,4 PT ≈ 5,95 m Opp(EFT) = 1/2 x basis x hoogte Opp(EFT) = 1/2 x EF x PT Opp(EFT) = 1/2 x 8,8 x √35,4 Opp(EFT) = 26,18 m2 |
FQ2 + QT2 = FT2 3,32 + QT2 = 7,42 QT2 = 43,87 QT = √43,87 QT ≈ 6,62 m Opp(FGT) = 1/2 x basis x hoogte Opp(FGT) = 1/2 x FG x QT Opp(FGT) = 1/2 x 6,6 x √43,87 Opp(FGT) = 21,86 m2 |

44.
Tip:
Bij a. Bereken FG met Pythagoras. Reken zelf na dat FG = 25.
Bij b. Bereken de lengte van de 'lichaamsdiagonaal' AG
a.Bij a. Bereken FG met Pythagoras. Reken zelf na dat FG = 25.
Bij b. Bereken de lengte van de 'lichaamsdiagonaal' AG
Oppervlakte totale glas = opp(ABFE) + opp(EFGH) + 2 x opp(FPG) + 2 x opp(BCPF)
opp(ABFE) = AB x BF = 3 x 1 = 3
opp(EFGH) = EF x FG = 3 x 2,5 = 7,5
opp(FPG) = 1/2 x basis x hoogte = 1/2 x FP x GP = 1/2 x 1,5 x 2 = 1,5
opp(BCPF) = BC x PC = 1,5 x 1 = 1,5
De totale oppervlakte = 3 + 7,5 + (2 x 1,5) + (2 x 1,5) = 3 + 7,5 + 3 + 3 = 16,5 m2
b.
Zie afbeelding:
AB2 + BC2 = AC2
32 + 1,52 = AC2
AC2 = 11,25
AC = √11,25
AC ≈ 3,35 meter
AC2 + CG2 = AG2
11,25 + 32 = AG2
AG2 = 20,25
AG = √20,25
AG = 4,5 meter
Aantal meter stang dat nodig is: 2 x AG = 2 x 4,5 = 9 meter.

45.
Tip:
BH en HJ zijn even lang. Het zijn 2 lichaamsdiagonalen in gelijke kubussen.
Als ∠BHJ rechthoekig is, dan moet de Stelling van Pythagoras kloppen in driehoek BHJ.
a.BH en HJ zijn even lang. Het zijn 2 lichaamsdiagonalen in gelijke kubussen.
Als ∠BHJ rechthoekig is, dan moet de Stelling van Pythagoras kloppen in driehoek BHJ.
Bereken eerst FH in driehoek EFH.
EF2 + EH2 = FH2
42 + 42 = FH2
FH2 = 32
FH = √32
FH ≈ 5,66 cm
FH2 + FJ2 = HJ2
32 + 42 = HJ2
HJ2 = 48
HJ = √48
HJ ≈ 6,93 cm
Dus BH = HJ = √48 ≈ 6,93 cm.
b.
Als ∠BHJ rechthoekig is, dan moet gelden:
BH2 + HJ2 = BJ2 (is dat wel zo?)
48 + 48 =(?) 82
96 =(?) 64
Nee, je ziet dat de Stelling van Pythagoras niet geldt. Dus ∠BHJ is niet rechthoekig.

46.
Tip:
Omdat P het midden is van GH weten we dus: AP = BP.
Bereken eerst AH en dan AP.
Kijk daarna of de Stelling van Pythagoras geldt in driehoek ABP.
Bereken eerst AH in driehoek ADH.Omdat P het midden is van GH weten we dus: AP = BP.
Bereken eerst AH en dan AP.
Kijk daarna of de Stelling van Pythagoras geldt in driehoek ABP.
AD2 + DH2 = AH2
42 + 32 = AH2
AH2 = 25
AH = √25
AH = 5
Bereken dan AP in driehoek AHP.
AH2 + HP2 = AP2
52 + 52 = AP2
AP2 = 50
AP = √50
AP ≈ 7,07
We hebben nu een "mogelijke" Pythagoras driehoek ABP.
Dan moet dus gelden:
AP2 + BP2 = AB2 (Is dat wel zo?)
(√50)2 + (√50)2 = 102 (?)
50 + 50 = 100 (?)
100 = 100
Ja, dat klopt zeker! Dus dan moet de hoek wel 90º zijn.
Dus driehoek ABP is rechthoekig.

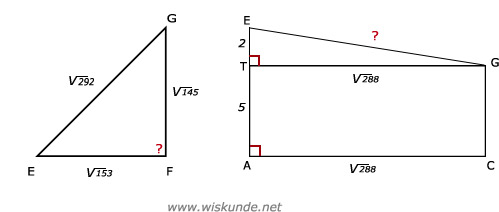
47.
Tip:
Bij a: Omtrek EFGH is: EF + FG + GH + EH
Gebruik dus 4x de Stelling van Pythagoras. Maak dus 4 rechthoekige driehoeken.
Bij b: Neem driehoek EFG en bepaal of hoek EFG 90º is. Bedenk: EG = √292.
a.Bij a: Omtrek EFGH is: EF + FG + GH + EH
Gebruik dus 4x de Stelling van Pythagoras. Maak dus 4 rechthoekige driehoeken.
Bij b: Neem driehoek EFG en bepaal of hoek EFG 90º is. Bedenk: EG = √292.
EF2 = 122 + 32
EF2 = 144 + 9
EF2 = 153
EF = √153
EF ≈ 12,37 m
FG2 = 122 + 12
FG2 = 144 + 1
FG2 = 145
FG = √145
FG ≈ 12,04 m
GH2 = 122 + 32
GH2 = 144 + 9
GH2 = 153
GH = √153
GH ≈ 12,37 m
EH2 = 122 + 12
EH2 = 144 + 1
EH2 = 145
EH = √145
EH ≈ 12,04 m
Dus omtrek EFGH = √153 + √145 + √153 + √145 = 48,82 meter. Dat is dus 488 dm.
b.
AC2 = AB2 + BC2
AC2 = 122 + 122
AC2 = 144 + 144
AC2 = 288
AC = √288
AC ≈ 16,97 m
Nu de vraag of geldt: EF2 + FG2 = EG2 (?)
(√153)2 + (√145)2 = (√292)2 (?)
153 + 145 = 292 (?)
298 = 292 (?)
Nee, dat klopt niet. Dus ∠EFG is niet recht. Dus kan EFGH nooit een rechthoek zijn.

48.
AP2 + MP2 = AM2
22 + 4,852 = AM2
AM2 = 27,5225
AM = √27,5225
AM ≈ 5,25 m
AM2 + MT2 = AT2
27,5225 + 3,52 = AT2
AT2 = 39,7725
AT = √39,7725
AT ≈ 6,31 m
b.
AP2 + PT2 = AT2
22 + PT2 = 39,7725
PT2 = 35,7725
PT = √35,7725
PT ≈ 5,98 m (hoogte driehoek)
Oppervlakte driehoek ABT = 1/2 x basis x hoogte
Oppervlakte driehoek ABT = 1/2 x AB x PT
Oppervlakte driehoek ABT = 1/2 x 4 x 5,98
Oppervlakte driehoek ABT = 11,96 m2
Dus de oppervlakte van het hele dak is: 8 x 11,96 m2 = 95,68 m2
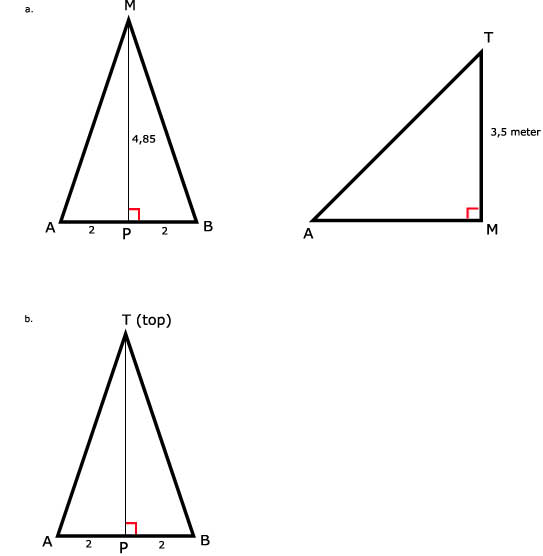
Tip:
AB = 32/8 = 4 meter
Driehoek ABM ligt horizontaal. M ligt recht onder T.
TM = 6 - 2,5 = 3,5
AF = 9,70 dus PM = 1/2 x 9,70 = 4,85
a.AB = 32/8 = 4 meter
Driehoek ABM ligt horizontaal. M ligt recht onder T.
TM = 6 - 2,5 = 3,5
AF = 9,70 dus PM = 1/2 x 9,70 = 4,85
AP2 + MP2 = AM2
22 + 4,852 = AM2
AM2 = 27,5225
AM = √27,5225
AM ≈ 5,25 m
AM2 + MT2 = AT2
27,5225 + 3,52 = AT2
AT2 = 39,7725
AT = √39,7725
AT ≈ 6,31 m
b.
AP2 + PT2 = AT2
22 + PT2 = 39,7725
PT2 = 35,7725
PT = √35,7725
PT ≈ 5,98 m (hoogte driehoek)
Oppervlakte driehoek ABT = 1/2 x basis x hoogte
Oppervlakte driehoek ABT = 1/2 x AB x PT
Oppervlakte driehoek ABT = 1/2 x 4 x 5,98
Oppervlakte driehoek ABT = 11,96 m2
Dus de oppervlakte van het hele dak is: 8 x 11,96 m2 = 95,68 m2

Andere paragrafen:
6.1. Rechthoekige driehoeken (1 t/m 9)
6.2. Het berekenen van schuine zijden (10 t/m 21)
6.3. Berekeningen met de stelling van Pythagoras (22 t/m 37)
6.4. Pythagoras in de ruimte (38 t/m 48)
6.5. Berekeningen in rechthoekige driehoeken (49 t/m 60)
6.6. Gemengde opgaven (61 t/m 66)
6.1. Rechthoekige driehoeken (1 t/m 9)
6.2. Het berekenen van schuine zijden (10 t/m 21)
6.3. Berekeningen met de stelling van Pythagoras (22 t/m 37)
6.4. Pythagoras in de ruimte (38 t/m 48)
6.5. Berekeningen in rechthoekige driehoeken (49 t/m 60)
6.6. Gemengde opgaven (61 t/m 66)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


