TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 6.3 Berekeningen met de stelling van Pythagoras VWO 2
Boek: Getal & Ruimte - De stelling van Pythagoras VWO 2 (deel 2) opgaven 22 t/m 37, 2009Met de Stelling van Pythagoras kun je naast de schuine zijde in een rechthoekige driehoek, ook 1 van de rechthoekszijde berekenen.
Stel de Stelling op en vul in wat je weet. Daaruit volgt de ontbrekende zijde.
Met de omgekeerde Stelling van Pythagoras werk je precies omgekeerd. Alle 3 de zijden zijn dan gegeven en je moet dan vaststellen of de hoek recht is.
Er moet dan zowel links als rechts van het =-teken hetzelfde staan. Is dat het geval, dan is de hoek dus 90º.
Stel de Stelling op en vul in wat je weet. Daaruit volgt de ontbrekende zijde.
Met de omgekeerde Stelling van Pythagoras werk je precies omgekeerd. Alle 3 de zijden zijn dan gegeven en je moet dan vaststellen of de hoek recht is.
Er moet dan zowel links als rechts van het =-teken hetzelfde staan. Is dat het geval, dan is de hoek dus 90º.
22.
b. Waar
c. Niet waar
d. Niet waar
e. Waar
f. Niet waar
23.
22 + QR2 = 32
4 + QR2 = 9
QR2 = 9 - 4
QR2 = 5
QR = √5
QR ≈ 2,2
DE2 + EF2 = DF2
DE2 + 12 = 42
DE2 + 1 = 16
DE2 = 16 - 1
DE2 = 15
DE = √15
DE ≈ 3,9
AC2 + BC2 = AB2
52 + BC2 = 62
25 + BC2 = 36
BC2 = 36 - 25
BC2 = 11
BC = √11
BC ≈ 3,3
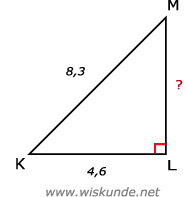
24.
4,62 + LM2 = 8,32
21,16 + LM2 = 68,89
LM2 = 68,89 - 21,16
LM2 = 47,73
LM = √47,73
LM ≈ 6,9 cm
25.
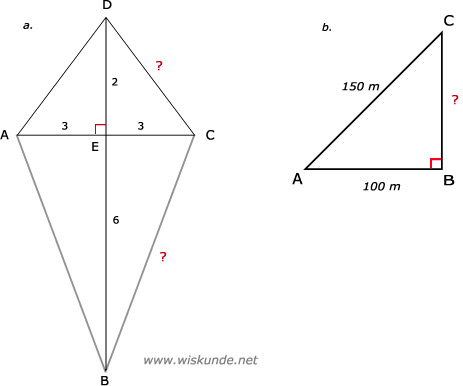
AD2 + CD2 = AC2
62 + CD2 = 102
36 + CD2 = 100
CD2 = 100 - 36
CD2 = 64
CD = √64
CD = 8 cm
b.
opp(ABC) = 1/2 x basis x hoogte
opp(ABC) = 1/2 x AB x CD
opp(ABC) = 1/2 x 12 x 8
opp(ABC) = 48 cm2
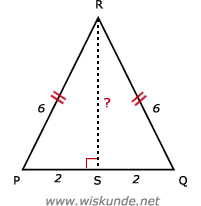
26.
22 + RS2 = 62
4 + RS2 = 36
RS2 = 36 - 4
RS2 = 32
RS = √32
RS ≈ 5,7
Dus de hoogte RS is 5,7 cm.
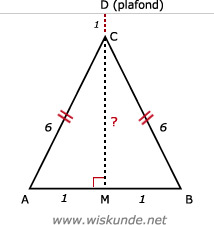
27.
12 + CM2 = 62
1 + CM2 = 36
CM2 = 36 - 1
CM2 = 35
CM = √35
CM ≈ 5,92 meter
Dus hoogte aula is 5,92 m + 1 m = 6,92 meter.
28.
BE2 + CE2 = BC2
62 + 32 = BC2
36 + 9 = BC2
BC2 = 45
BC = √45
BC ≈ 6,71 dm
CE2 + DE2 = CD2
32 + 22 = CD2
9 + 4 = CD2
CD2 = 13
CD = √13
CD ≈ 3,61 dm
Totale lengte van het groene touw = 6,71 + 6,71 + 3,61 + 3,61 = 20,64 dm. Dat is 206,4 cm.
b.
AB2 + BC2 = AC2
1002 + BC2 = 1502
10000 + BC2 = 22500
BC2 = 22500 - 10000
BC2 = 12500
BC = √12500
BC ≈ 111,80 m
Dus de hoogte van de vlieger is 111,8 meter.
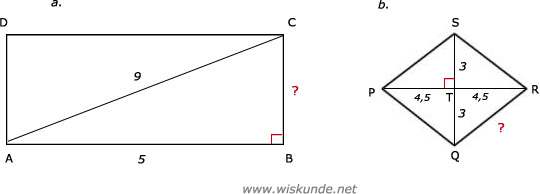
29.
AB2 + BC2 = AC2
52 + BC2 = 92
25 + BC2 = 81
BC2 = 81 - 25
BC2 = 56
BC = √56
BC ≈ 7,5 cm
b.
QT2 + RT2 = QR2
32 + 4,52 = QR2
QR2 = 29,25
QR = √29,25
QR ≈ 5,41
Omtrek ruit PQRS = 4 x QR = 4 x 5,41 = 21,6 cm.
30.
AF2 + BF2 = AB2
AF2 + 4,82 = 82
AF2 + 23,04 = 64
AF2 = 64 - 23,04
AF2 = 40,96
AF = √40,96
AF = 6,4
AE2 + DE2 = AD2
AE2 + 4,82 = 62
AE2 + 23,04 = 36
AE2 = 36 - 23,04
AE2 = 12,96
AE = √12,96
AE = 3,6
EF = AF - AE = 6,4 - 3,6 = 2,8 cm
b.
opp(ABF) = 1/2 x basis x hoogte
opp(ABF) = 1/2 x AF x BF
opp(ABF) = 1/2 x 6,4 x 4,8
opp(ABF) = 15,36 cm2
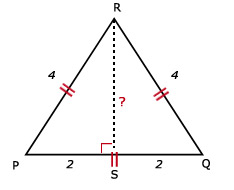
31.
22 + RS2 = 42
RS2 = 16 - 4
RS2 = 12
RS = √12
RS ≈ 3,46 cm
Opp(PQR) = 1/2 x basis x hoogte
Opp(PQR) = 1/2 x PQ x RS
Opp(PQR) = 1/2 x 4 x √12
Opp(PQR) = 2√12
Opp(PQR) ≈ 6,93 cm2
Tip:
Stel eerst op basis van de driehoek de Stelling van Pythagoras op. Bekijk dan welke bewering juist kan zijn.
a. Niet waarStel eerst op basis van de driehoek de Stelling van Pythagoras op. Bekijk dan welke bewering juist kan zijn.
b. Waar
c. Niet waar
d. Niet waar
e. Waar
f. Niet waar
23.
Tip:
Schrijf eerst de Stelling van elke driehoek goed op. Vul in wat je weet.
PQ2 + QR2 = PR2Schrijf eerst de Stelling van elke driehoek goed op. Vul in wat je weet.
22 + QR2 = 32
4 + QR2 = 9
QR2 = 9 - 4
QR2 = 5
QR = √5
QR ≈ 2,2
DE2 + EF2 = DF2
DE2 + 12 = 42
DE2 + 1 = 16
DE2 = 16 - 1
DE2 = 15
DE = √15
DE ≈ 3,9
AC2 + BC2 = AB2
52 + BC2 = 62
25 + BC2 = 36
BC2 = 36 - 25
BC2 = 11
BC = √11
BC ≈ 3,3
24.
Tip:
Maak eerst een schets met ∠L = 90º.
KL2 + LM2 = KM2Maak eerst een schets met ∠L = 90º.
4,62 + LM2 = 8,32
21,16 + LM2 = 68,89
LM2 = 68,89 - 21,16
LM2 = 47,73
LM = √47,73
LM ≈ 6,9 cm

25.
Tip:
- oppervlakte driehoek = 1/2 x basis x hoogte
- driehoek ABC is een gelijkbenige driehoek met AC = BC = 10
- CD is de symmetrieas
- AD = 1/2 x AB
a.- oppervlakte driehoek = 1/2 x basis x hoogte
- driehoek ABC is een gelijkbenige driehoek met AC = BC = 10
- CD is de symmetrieas
- AD = 1/2 x AB
AD2 + CD2 = AC2
62 + CD2 = 102
36 + CD2 = 100
CD2 = 100 - 36
CD2 = 64
CD = √64
CD = 8 cm
b.
opp(ABC) = 1/2 x basis x hoogte
opp(ABC) = 1/2 x AB x CD
opp(ABC) = 1/2 x 12 x 8
opp(ABC) = 48 cm2
26.
Tip:
Driehoek PQR is een gelijkbenige driehoek.
Teken de hoogtelijn RS.
PS2 + RS2 = PR2Driehoek PQR is een gelijkbenige driehoek.
Teken de hoogtelijn RS.
22 + RS2 = 62
4 + RS2 = 36
RS2 = 36 - 4
RS2 = 32
RS = √32
RS ≈ 5,7
Dus de hoogte RS is 5,7 cm.

27.
Tip:
Bereken eerst MC. Tel daar 1 meter bij op en je hebt de hoogte van de aula (DM).
In een schets hoeven de afmetingen niet precies te kloppen. Daarom is het ook een schets!
AM2 + CM2 = AC2Bereken eerst MC. Tel daar 1 meter bij op en je hebt de hoogte van de aula (DM).
In een schets hoeven de afmetingen niet precies te kloppen. Daarom is het ook een schets!
12 + CM2 = 62
1 + CM2 = 36
CM2 = 36 - 1
CM2 = 35
CM = √35
CM ≈ 5,92 meter
Dus hoogte aula is 5,92 m + 1 m = 6,92 meter.

28.
Tip:
Bij a: bereken eerst BC en CD door 2x de Stelling van Pythagoras te gebruiken.
a.Bij a: bereken eerst BC en CD door 2x de Stelling van Pythagoras te gebruiken.
BE2 + CE2 = BC2
62 + 32 = BC2
36 + 9 = BC2
BC2 = 45
BC = √45
BC ≈ 6,71 dm
CE2 + DE2 = CD2
32 + 22 = CD2
9 + 4 = CD2
CD2 = 13
CD = √13
CD ≈ 3,61 dm
Totale lengte van het groene touw = 6,71 + 6,71 + 3,61 + 3,61 = 20,64 dm. Dat is 206,4 cm.
b.
AB2 + BC2 = AC2
1002 + BC2 = 1502
10000 + BC2 = 22500
BC2 = 22500 - 10000
BC2 = 12500
BC = √12500
BC ≈ 111,80 m
Dus de hoogte van de vlieger is 111,8 meter.

29.
Tip:
Bij opgave b: in een ruit delen de diagonalen elkaar loodrecht middendoor (eigenschap van een ruit).
a.Bij opgave b: in een ruit delen de diagonalen elkaar loodrecht middendoor (eigenschap van een ruit).
AB2 + BC2 = AC2
52 + BC2 = 92
25 + BC2 = 81
BC2 = 81 - 25
BC2 = 56
BC = √56
BC ≈ 7,5 cm
b.
QT2 + RT2 = QR2
32 + 4,52 = QR2
QR2 = 29,25
QR = √29,25
QR ≈ 5,41
Omtrek ruit PQRS = 4 x QR = 4 x 5,41 = 21,6 cm.

30.
Tip:
Bereken eerst AF in driehoek ABF.
Bereken dan AE in driehoek AED.
Dan EF = AF - AE
a.Bereken eerst AF in driehoek ABF.
Bereken dan AE in driehoek AED.
Dan EF = AF - AE
AF2 + BF2 = AB2
AF2 + 4,82 = 82
AF2 + 23,04 = 64
AF2 = 64 - 23,04
AF2 = 40,96
AF = √40,96
AF = 6,4
AE2 + DE2 = AD2
AE2 + 4,82 = 62
AE2 + 23,04 = 36
AE2 = 36 - 23,04
AE2 = 12,96
AE = √12,96
AE = 3,6
EF = AF - AE = 6,4 - 3,6 = 2,8 cm
b.
opp(ABF) = 1/2 x basis x hoogte
opp(ABF) = 1/2 x AF x BF
opp(ABF) = 1/2 x 6,4 x 4,8
opp(ABF) = 15,36 cm2
31.
Tip:
Gelijkbenige driehoek dus PQ = QR = PR = 4
Trek de hulplijn RS
PS = QS = 2
Bereken de hoogte RS
PS2 + RS2 = PR2Gelijkbenige driehoek dus PQ = QR = PR = 4
Trek de hulplijn RS
PS = QS = 2
Bereken de hoogte RS
22 + RS2 = 42
RS2 = 16 - 4
RS2 = 12
RS = √12
RS ≈ 3,46 cm
Opp(PQR) = 1/2 x basis x hoogte
Opp(PQR) = 1/2 x PQ x RS
Opp(PQR) = 1/2 x 4 x √12
Opp(PQR) = 2√12
Opp(PQR) ≈ 6,93 cm2

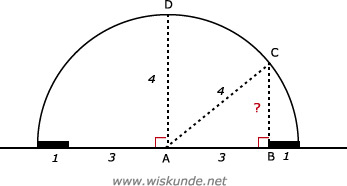
32.
32 + BC2 = 42
BC2 = 16 - 9
BC2 = 7
BC = √7
BC ≈ 2,6 meter
Dus de maximale hoogte van de camper (bij BC) is 2,6 meter.
33.
Geldt: KM2 + LM2 =(?) KL2
122 + 152 =(?) 192
144 + 225 = 361
369 = 361
Nee, dit klopt niet. Dus driehoek KLM is geen rechthoekige driehoek.
b.
Geldt: PQ2 + PR2 =(?) QR2
352 + 122 =(?) 372
1225 + 144 = 1369
1369 = 1369
Ja, dit klopt. Dus driehoek PQR is een rechthoekige driehoek. De rechte hoek is ∠P.
c.
Geldt: BC2 + AC2 =(?) AB2
12,52 + 302 =(?) 33,752
156,25 + 900 = 1139,0625
1056,25 = 1139,0625
Nee, dit klopt niet. Dus driehoek ABC is geen rechthoekige driehoek.
34.
42 + 32 = AB2
AB2 = 16 + 9
AB2 = 25
AB = √25
AB = 5
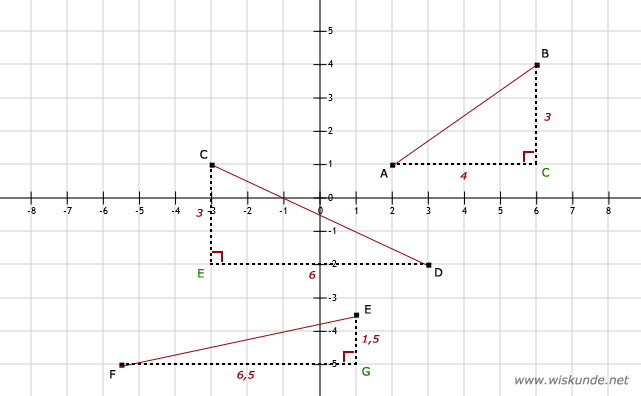
35.
c.
FG2 + EG2 = EF2
6,52 + 1,52 = EF2
EF2 = 44,5
EF = √44,5
EF ≈ 6,67
36.
c.
22 + 62 = BE2
4 + 36 = BE2
BE2 = 40
BE = √40
BE ≈ 6,3
37.
KL2 = 32 + 62 => KL2 = 45 => KL = √45
LM2 = 12 + 42 => LM2 = 17 => LM = √17
MN2 = 12 + 22 => MN2 = 5 => MN = √5
KN2 = 22 + 32 => KN2 = 13 => KN = √13
Omtrek vierhoek KLMN = √45 + √17 + √5 + √13 ≈ 16,7
Vierhoek PQRS:
PQ2 = 12 + 22 => PQ2 = 5 => PQ = √5
QR2 = 12 + 62 => QR2 = 37 => QR = √37
RS2 = 22 + 42 => RS2 = 20 => RS = √20
PS2 = 12 + 32 => PS2 = 10 => PS = √10
Omtrek vierhoek PQRS = √5 + √37 + √20 + √10 ≈ 16,0
Tip:
Maak een goede schets met AB = 3. AB is de maximale breedte van de rechter weghelft.
AC is 1/2 x diameter
AD = AC = 4 is de straal van de cirkel
Bereken hoogte BC in driehoek ABC
AB2 + BC2 = AC2Maak een goede schets met AB = 3. AB is de maximale breedte van de rechter weghelft.
AC is 1/2 x diameter
AD = AC = 4 is de straal van de cirkel
Bereken hoogte BC in driehoek ABC
32 + BC2 = 42
BC2 = 16 - 9
BC2 = 7
BC = √7
BC ≈ 2,6 meter
Dus de maximale hoogte van de camper (bij BC) is 2,6 meter.

33.
Tip:
De hoek tegenover de langste zijde is mogelijk een rechte hoek.
Schrijf de Stelling van Pythagoras op en kijk of het klopt.
Zoja, dan is de hoek recht. Zo nee, dan is de hoek niet recht.
a.De hoek tegenover de langste zijde is mogelijk een rechte hoek.
Schrijf de Stelling van Pythagoras op en kijk of het klopt.
Zoja, dan is de hoek recht. Zo nee, dan is de hoek niet recht.
Geldt: KM2 + LM2 =(?) KL2
122 + 152 =(?) 192
144 + 225 = 361
369 = 361
Nee, dit klopt niet. Dus driehoek KLM is geen rechthoekige driehoek.
b.
Geldt: PQ2 + PR2 =(?) QR2
352 + 122 =(?) 372
1225 + 144 = 1369
1369 = 1369
Ja, dit klopt. Dus driehoek PQR is een rechthoekige driehoek. De rechte hoek is ∠P.
c.
Geldt: BC2 + AC2 =(?) AB2
12,52 + 302 =(?) 33,752
156,25 + 900 = 1139,0625
1056,25 = 1139,0625
Nee, dit klopt niet. Dus driehoek ABC is geen rechthoekige driehoek.
34.
Tip:
Het is een 3-4-5 driehoek
OA2 + OB2 = AB2Het is een 3-4-5 driehoek
42 + 32 = AB2
AB2 = 16 + 9
AB2 = 25
AB = √25
AB = 5
35.
Tip:
Teken de lijnstukken en maak een Pythagoras driehoek.
Teken de lijnstukken en maak een Pythagoras driehoek.
|
a. AC2 + BC2 = AB2 42 + 32 = AB2 AB2 = 16 + 9 AB2 = 25 AB = √25 AB = 5 |
b. DE2 + CE2 = CD2 62 + 32 = CD2 CD2 = 36 + 9 CD2 = 45 CD = √45 CD ≈ 6,71 |
FG2 + EG2 = EF2
6,52 + 1,52 = EF2
EF2 = 44,5
EF = √44,5
EF ≈ 6,67

36.
Tip:
Zoek een Pythagoras driehoek en schrijf de stelling goed op. Elk hokje is 1 cm.
Zoek een Pythagoras driehoek en schrijf de stelling goed op. Elk hokje is 1 cm.
|
a. 52 + 52 = AD2 25 + 25 = AD2 AD2 = 50 AD = √50 AD ≈ 7,1 |
b. 52 + 32 = CF2 25 + 9 = CF2 CF2 = 34 CF = √34 CF ≈ 5,8 |
22 + 62 = BE2
4 + 36 = BE2
BE2 = 40
BE = √40
BE ≈ 6,3
37.
Tip:
Zoek de juiste Pythagoras driehoeken en schrijf de stelling goed op. Elk hokje is 1 cm.
Vierhoek KLMN:Zoek de juiste Pythagoras driehoeken en schrijf de stelling goed op. Elk hokje is 1 cm.
KL2 = 32 + 62 => KL2 = 45 => KL = √45
LM2 = 12 + 42 => LM2 = 17 => LM = √17
MN2 = 12 + 22 => MN2 = 5 => MN = √5
KN2 = 22 + 32 => KN2 = 13 => KN = √13
Omtrek vierhoek KLMN = √45 + √17 + √5 + √13 ≈ 16,7
Vierhoek PQRS:
PQ2 = 12 + 22 => PQ2 = 5 => PQ = √5
QR2 = 12 + 62 => QR2 = 37 => QR = √37
RS2 = 22 + 42 => RS2 = 20 => RS = √20
PS2 = 12 + 32 => PS2 = 10 => PS = √10
Omtrek vierhoek PQRS = √5 + √37 + √20 + √10 ≈ 16,0
Andere paragrafen:
6.1. Rechthoekige driehoeken (1 t/m 9)
6.2. Het berekenen van schuine zijden (10 t/m 21)
6.3. Berekeningen met de stelling van Pythagoras (22 t/m 37)
6.4. Pythagoras in de ruimte (38 t/m 48)
6.5. Berekeningen in rechthoekige driehoeken (49 t/m 60)
6.6. Gemengde opgaven (61 t/m 66)
6.1. Rechthoekige driehoeken (1 t/m 9)
6.2. Het berekenen van schuine zijden (10 t/m 21)
6.3. Berekeningen met de stelling van Pythagoras (22 t/m 37)
6.4. Pythagoras in de ruimte (38 t/m 48)
6.5. Berekeningen in rechthoekige driehoeken (49 t/m 60)
6.6. Gemengde opgaven (61 t/m 66)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


