TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 2.3 Doorsneden VMBO 3 KGT
Boek: Getal & Ruimte - Kaart en doorsnede VMBO 3 (deel 1) opgaven 42 t/m 61, 2010Ieder ruimtefiguur kun je doorsnijden. Het snijvlak noemen we de doorsnede.
De doorsnede is altijd een plat figuur. Als je bijvoorbeeld een cilinder horizontaal doorsnijdt, is de doorsnede een cirkel.
Als je een cilinder schuin doorsnijdt, is de doorsnede een ellips. Andere vormen van doorsneden kunnen zijn: vierkant, rechthoek, driehoek enz.
De doorsnede is altijd een plat figuur. Als je bijvoorbeeld een cilinder horizontaal doorsnijdt, is de doorsnede een cirkel.
Als je een cilinder schuin doorsnijdt, is de doorsnede een ellips. Andere vormen van doorsneden kunnen zijn: vierkant, rechthoek, driehoek enz.
42.
43.
b.
TM = √29 ≈ 5,4 cm
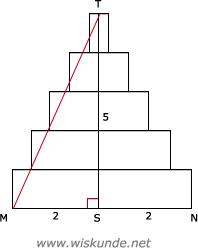
44.
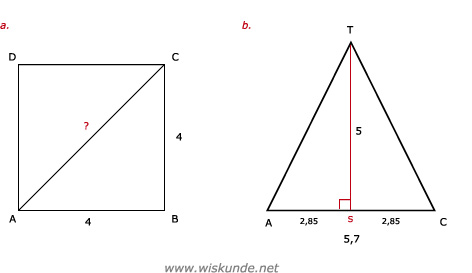
45.
Inhoud piramide = 26,7 cm3
46.
a. De ruimtefiguur die erbij hoort is een kegel.
b. Zie afbeelding
c.
PT = √512 ≈ 22,6
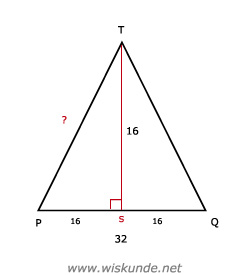
47.
cilinder a: doorsnede 4
cilinder b: doorsnede 5
cilinder c: doorsnede 6
cilinder d: doorsnede 1
cilinder e: doorsnede 2
cilinder f: doorsnede 3
b. Verticale doorsneden zijn: 1 en 4
c. Horizontale doorsnede is: 5
48.
De 3 doorsneden (vierkanten) horen bij een piramide.
49.
Bij een balk, kubus en een cilinder zijn alle horizontale doorsneden even groot.
50.
De ruimtefiguren die een cirkel als doorsnede kunnen hebben, zijn: een bol, een cilinder en een kegel.
51.
Zie afbeelding
Tip:
Bij een hoogtekaartje kijk je als het ware er bovenop.
De piramide is 5 cm hoog.Bij een hoogtekaartje kijk je als het ware er bovenop.
43.
Tip:
De Stelling van Pythagoras kan alleen in een rechthoekige driehoek.
a. Zie afbeeldingDe Stelling van Pythagoras kan alleen in een rechthoekige driehoek.
b.
| -> kwadraat | ||
| MS = 2 | | | 4 |
| ST = 5 | | | 25 |
| ----------- + | ||
| TM = ? | | | 29 |
| <- wortel |
TM = √29 ≈ 5,4 cm

44.
Tip:
Maak een schets.
ABCD is een vierkant. Dus AB = BC = 4.
Maak een schets.
ABCD is een vierkant. Dus AB = BC = 4.
a. Zie afbeelding
AC = √32 ≈ 5,7 cm |
b. Zie afbeelding
AT = √33,1225 ≈ 5,8 cm |

45.
Tip:
Inhoud piramide = 1/3 x oppervlakte grondvlak x hoogte
Inhoud piramide = 1/3 x 4 x 4 x 5Inhoud piramide = 1/3 x oppervlakte grondvlak x hoogte
Inhoud piramide = 26,7 cm3
46.
a. De ruimtefiguur die erbij hoort is een kegel.
b. Zie afbeelding
c.
| -> kwadraat | ||
| PS = 16 | | | 256 |
| ST = 16 | | | 256 |
| ----------- + | ||
| PT = ? | | | 512 |
| <- wortel |
PT = √512 ≈ 22,6

47.
Tip:
Als je een cilinder verticaal doorsnijdt, is de doorsnede een rechthoek.
a.Als je een cilinder verticaal doorsnijdt, is de doorsnede een rechthoek.
cilinder a: doorsnede 4
cilinder b: doorsnede 5
cilinder c: doorsnede 6
cilinder d: doorsnede 1
cilinder e: doorsnede 2
cilinder f: doorsnede 3
b. Verticale doorsneden zijn: 1 en 4
c. Horizontale doorsnede is: 5
48.
De 3 doorsneden (vierkanten) horen bij een piramide.
49.
Bij een balk, kubus en een cilinder zijn alle horizontale doorsneden even groot.
50.
De ruimtefiguren die een cirkel als doorsnede kunnen hebben, zijn: een bol, een cilinder en een kegel.
51.
Zie afbeelding

52.
b. Een rechthoek
c. Ribbe BF is 4 cm.
d. Langer, want HF is de schuine zijde van de rechthoekige driehoek EFH en de schuine zijde is altijd de langste zijde.
53.
BG = √32 ≈ 5,7 CM
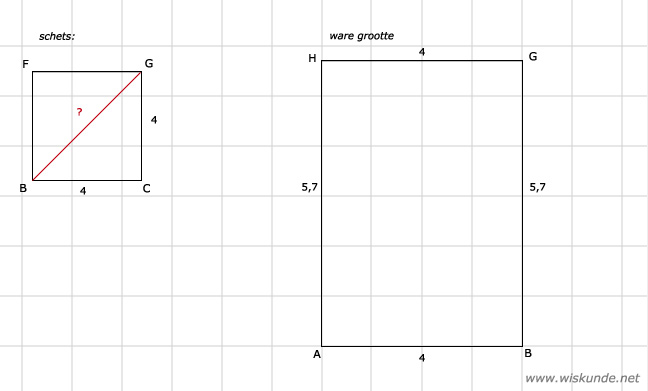
54.
LR = √41 ≈ 6,4 cm
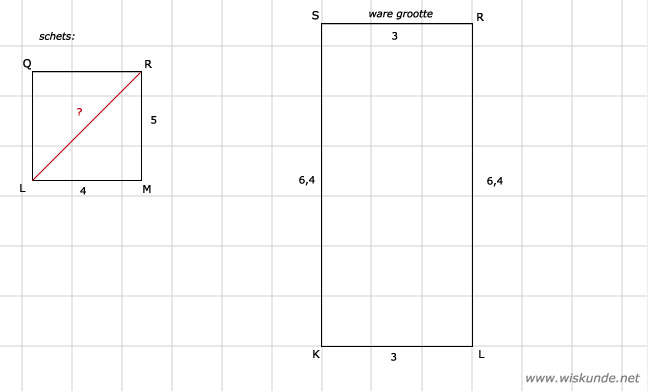
55.
1. DBFH
2. ACGE
3. DAFG
4. ABGH
5. EDCF
6. BCHE
b. Ja
c.
DB = √50 ≈ 7,1 cm
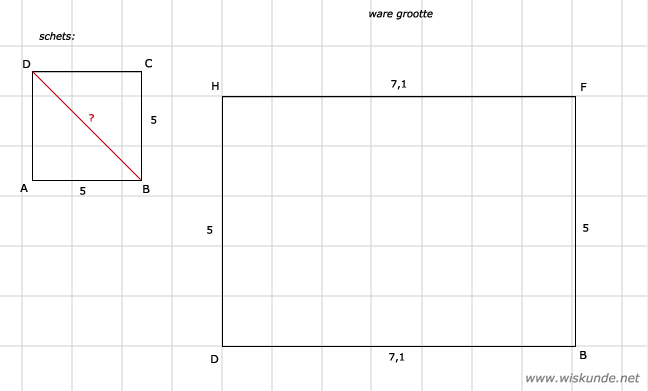
56.
c. Nee
57.
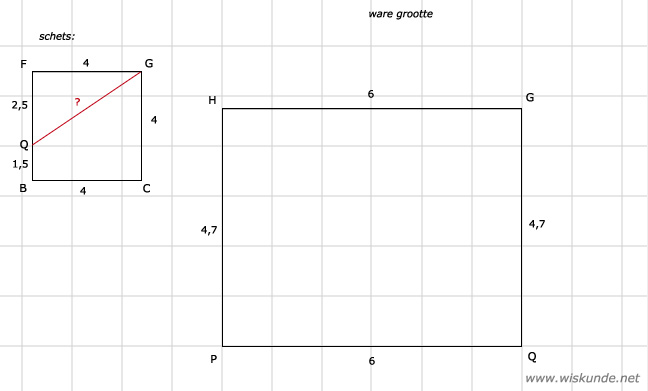
b.
GQ = √22,25 ≈ 4,7 cm
c. PQ = 6
d. Zie afbeelding
58.
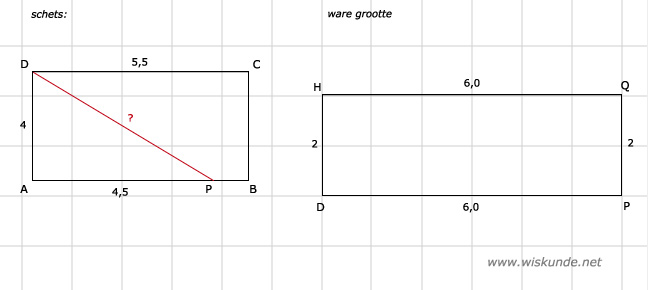
DP = √36,25 ≈ 6,0 cm
59.
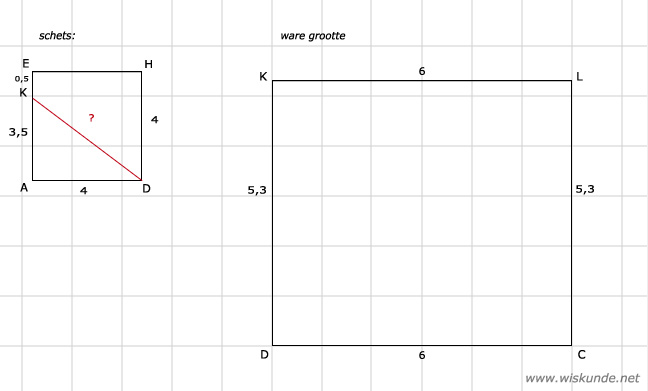
DK = √28,25 ≈ 5,3 cm
60.
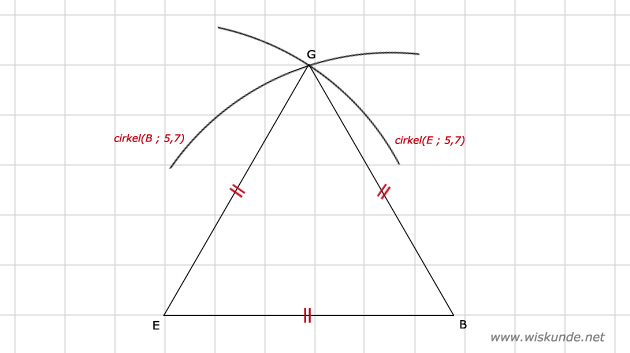
BE = √32 ≈ 5,7 cm
61.
Tip:
In een rechthoekige driehoek is de schuine zijde altijd het langst.
a. Het is een vlak door de diagonalen van het boven- en ondervlak.In een rechthoekige driehoek is de schuine zijde altijd het langst.
b. Een rechthoek
c. Ribbe BF is 4 cm.
d. Langer, want HF is de schuine zijde van de rechthoekige driehoek EFH en de schuine zijde is altijd de langste zijde.
53.
Tip:
Bereken eerst BG met de Stelling van Pythagoras.
Bereken eerst BG met de Stelling van Pythagoras.
| -> kwadraat | ||
| BC = 4 | | | 16 |
| CG = 4 | | | 16 |
| ----------- + | ||
| BG = ? | | | 32 |
| <- wortel |
BG = √32 ≈ 5,7 CM

54.
Tip:
Bereken eerst LR met de Stelling van Pythagoras.
Bij een schets hoeven de afmetingen niet te kloppen.
Bereken eerst LR met de Stelling van Pythagoras.
Bij een schets hoeven de afmetingen niet te kloppen.
| -> kwadraat | ||
| LM = 4 | | | 16 |
| RM = 5 | | | 25 |
| ----------- + | ||
| LR = ? | | | 41 |
| <- wortel |
LR = √41 ≈ 6,4 cm

55.
Tip:
Bij c: Bereken eerst DB met de Stelling van Pythagoras.
a. Bij c: Bereken eerst DB met de Stelling van Pythagoras.
1. DBFH
2. ACGE
3. DAFG
4. ABGH
5. EDCF
6. BCHE
b. Ja
c.
| -> kwadraat | ||
| AB = 5 | | | 25 |
| AD = 5 | | | 25 |
| ----------- + | ||
| DB = ? | | | 50 |
| <- wortel |
DB = √50 ≈ 7,1 cm

56.
Tip:
Bij a: Bereken eerst AC met de Stelling van Pythagoras.
Bij b: Bereken eerst FC met de Stelling van Pythagoras.
Bij een schets hoeven de afmetingen niet te kloppen.
Bij a: Bereken eerst AC met de Stelling van Pythagoras.
Bij b: Bereken eerst FC met de Stelling van Pythagoras.
Bij een schets hoeven de afmetingen niet te kloppen.
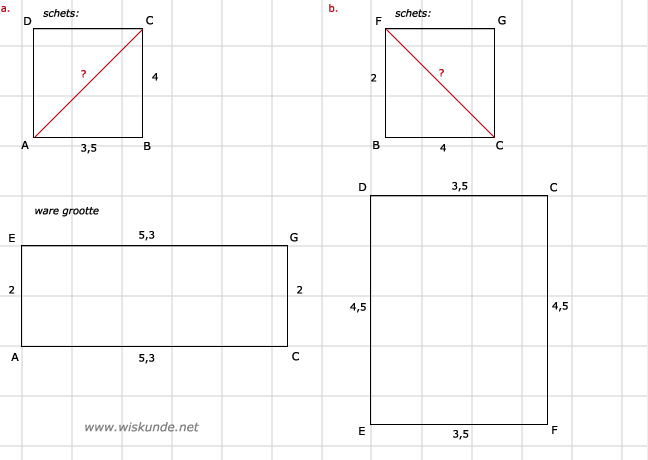
a. Zie afbeelding
AC = √28,25 ≈ 5,3 cm |
b. Zie afbeelding
FC = √20 ≈ 4,5 cm |

57.
Tip:
Bereken eerst GQ met de Stelling van Pythagoras.
a. Zie afbeeldingBereken eerst GQ met de Stelling van Pythagoras.
b.
| -> kwadraat | ||
| FQ = 2,5 | | | 6,25 |
| FG = 4 | | | 16 |
| ----------- + | ||
| GQ = ? | | | 22,25 |
| <- wortel |
GQ = √22,25 ≈ 4,7 cm
c. PQ = 6
d. Zie afbeelding

58.
Tip:
Bereken eerst DP met de Stelling van Pythagoras.
∠DAP = 90º
PQ = 2
Bereken eerst DP met de Stelling van Pythagoras.
∠DAP = 90º
PQ = 2
| -> kwadraat | ||
| AP = 4,5 | | | 20,25 |
| AD = 4 | | | 16 |
| ----------- + | ||
| DP = ? | | | 36,25 |
| <- wortel |
DP = √36,25 ≈ 6,0 cm

59.
Tip:
Bereken eerst DK met de Stelling van Pythagoras.
Bereken eerst DK met de Stelling van Pythagoras.
| -> kwadraat | ||
| AK = 3,5 | | | 12,25 |
| AD = 4 | | | 16 |
| ----------- + | ||
| DK = ? | | | 28,25 |
| <- wortel |
DK = √28,25 ≈ 5,3 cm

60.
Tip:
Gegeven een kubus. Dus: BE = EG = BG want deze diagonalen zijn even lang.
De doorsnede is dus een gelijkzijdige driehoek EBG.
Punt G van de doorsnede is het snijpunt van 2 cirkels met straal BE.
Bereken eerst BE met Pythagoras.
Gegeven een kubus. Dus: BE = EG = BG want deze diagonalen zijn even lang.
De doorsnede is dus een gelijkzijdige driehoek EBG.
Punt G van de doorsnede is het snijpunt van 2 cirkels met straal BE.
Bereken eerst BE met Pythagoras.
| -> kwadraat | ||
| AB = 4 | | | 16 |
| AE = 4 | | | 16 |
| ----------- + | ||
| BE = ? | | | 32 |
| <- wortel |
BE = √32 ≈ 5,7 cm

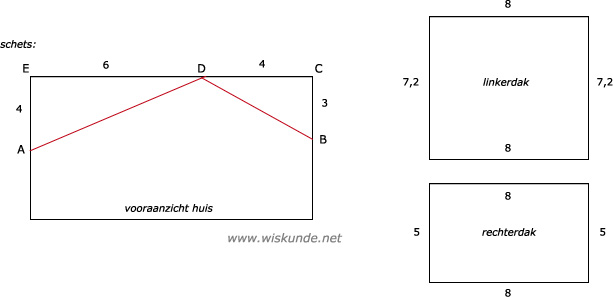
61.
Berekening AD van linkerdak:
AD = √52 ≈ 7,2 |
Berekening BD van rechterdak:
BD = √25 = 5 |

Andere paragrafen:
2.1. Koers en kaart (1 t/m 24)
2.2. Hoogtelijnen (25 t/m 41)
2.3. Doorsneden (42 t/m 61)
2.4. Pythagoras in de ruimte (62 t/m 65)
2.5. Aanzichten (66 t/m 72)
2.1. Koers en kaart (1 t/m 24)
2.2. Hoogtelijnen (25 t/m 41)
2.3. Doorsneden (42 t/m 61)
2.4. Pythagoras in de ruimte (62 t/m 65)
2.5. Aanzichten (66 t/m 72)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


