TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 3.1 Evenredig en omgekeerd evenredig VMBO 4 KGT
Boek: Getal & Ruimte - Verbanden 2 VMBO 4 (deel 1) opgaven 1 t/m 15, 2011Wat is omgekeerd evenredig?
Als je een bedrag door meerdere mensen deelt, dan daalt de prijs per persoon.
Er is dan een verband tussen het bedrag en het aantal personen.
We noemen dit dan een omgekeerd evenredig verband.
De grafiek die we hierbij kunnen tekenen, noemen we een hyperbool.
Voorbeeld van een omgekeerd evenredig verband: Bedrag in euro = 1200 / aantal personen
In het kort: B = 1200 / p
Als je een bedrag door meerdere mensen deelt, dan daalt de prijs per persoon.
Er is dan een verband tussen het bedrag en het aantal personen.
We noemen dit dan een omgekeerd evenredig verband.
De grafiek die we hierbij kunnen tekenen, noemen we een hyperbool.
Voorbeeld van een omgekeerd evenredig verband: Bedrag in euro = 1200 / aantal personen
In het kort: B = 1200 / p
1.
a. Als er 20 leerlingen meegaan: €1000,= / 20 leerlingen = €50,= per leerling
b. Als er 40 leerlingen meegaan: €1000,= / 40 leerlingen = €25,= per leerling
c. Als er 55 leerlingen meegaan: €1000,= / 55 leerlingen = €18,18 per leerling
d. Hoe meer leerlingen er meegaan, hoe minder het per persoon kost.
2.
b.
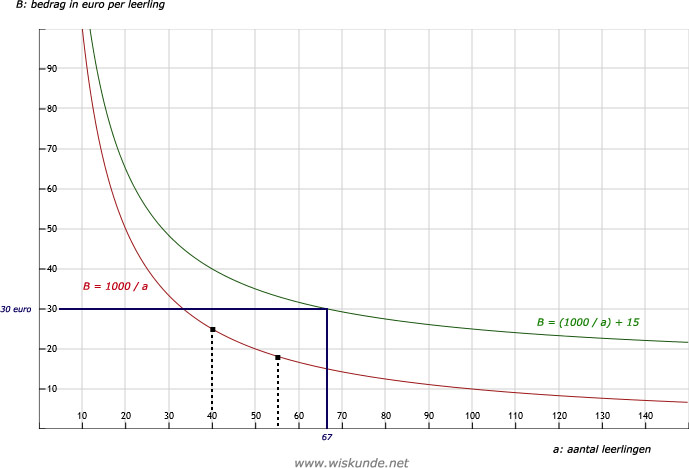
Zie afbeelding (rode grafiek)
c. Zie het gedeelte van de rode grafiek tussen de stippellijntjes.
3.
a.
Entree is 15 euro.
b.
c.
Zie afbeelding (groene grafiek): bij 30 euro hoort 67 leerlingen.
d. B = (1000 / 51) + 15 = 34,61 euro
4.
b.
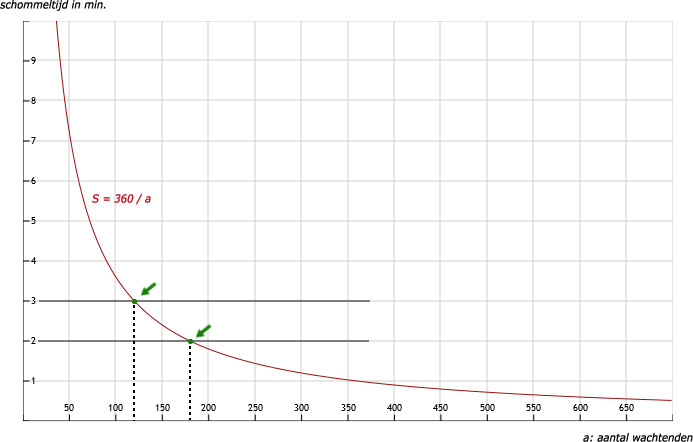
Bij a = 20 krijgen we: schommeltijd = 360 / 20 = 18 minuten
c.
Bij a = 240 krijgen we: schommeltijd = 360 / 240 = 1,5 minuut
5.
b. Bij a = 360 krijgen we: schommeltijd = 360 / 360 = 1 minuut
c. *
6.
b.
c.
Ze zijn gelijk.
7.
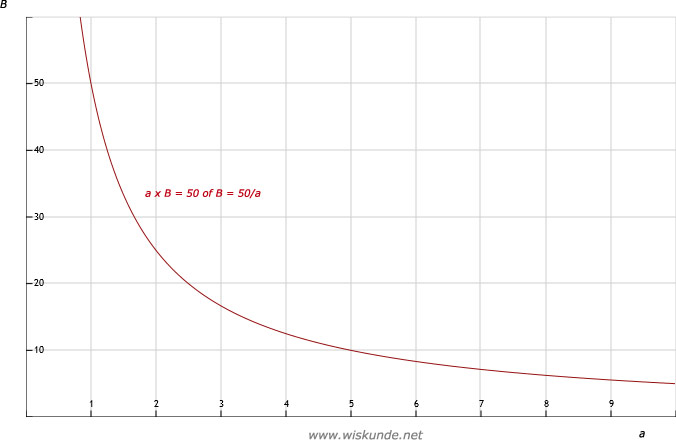
10 x B = 50 => B = 5
Dus bedrag per persoon is €5,=.
b.
c. Zie afbeelding
d. B = 50 / a
8.
a x G = 2400
12 x G = 2400
G = 2400 / 12 = 200 gram
b.
a x G = 2400
a x 600 = 2400
a = 2400 / 600
a = 4 personen
c.
G = 2400 / a (links en rechts delen door 'a')
9.
b.
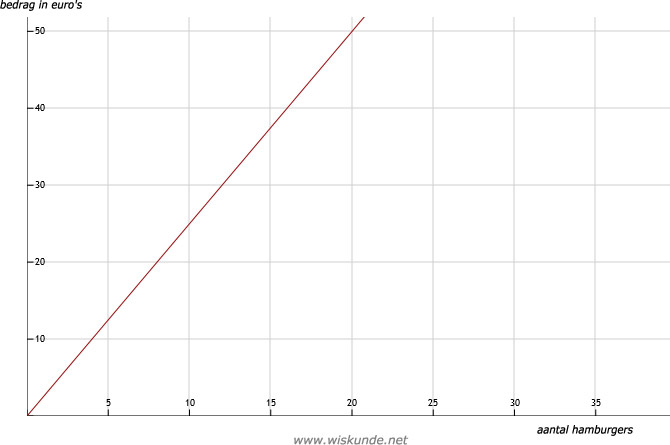
c. Hoe meer hamburgers je koopt, hoe meer je moet betalen.
d. Als je 4x zoveel hamburgers koopt, moet je ook 4x zoveel betalen.
e. Zie afbeelding
10.
Dus er is sprake van een omgekeerd evenredig verband.
b. Als a 3x zo groot wordt (zie 3 -> 9) dan wordt N ook 3x zo groot (8 -> 24).
Dus er is sprake van een evenredig verband.
c. Bij tabel I hoort een hyperbool, bij tabel II hoort een rechte lijn.
d. Tabel I:
Tabel II:
a. Als er 20 leerlingen meegaan: €1000,= / 20 leerlingen = €50,= per leerling
b. Als er 40 leerlingen meegaan: €1000,= / 40 leerlingen = €25,= per leerling
c. Als er 55 leerlingen meegaan: €1000,= / 55 leerlingen = €18,18 per leerling
d. Hoe meer leerlingen er meegaan, hoe minder het per persoon kost.
2.
Tip:
Hoe groter het aantal leerlingen (a), des te lager het bedrag (B).
Neem a maar eens 100.000 leerlingen. Dan is de prijs per leerling (B) nog maar 0,01. Dat is 1 eurocent.
Dus hoe verder de grafiek naar rechts gaat, hoe meer de prijs naar 0 gaat.
a.Hoe groter het aantal leerlingen (a), des te lager het bedrag (B).
Neem a maar eens 100.000 leerlingen. Dan is de prijs per leerling (B) nog maar 0,01. Dat is 1 eurocent.
Dus hoe verder de grafiek naar rechts gaat, hoe meer de prijs naar 0 gaat.
| a | 10 | 20 | 30 | 40 | 50 | 55 | 60 | 100 | 1000 |
| B | 100 | 50 | 33,3 | 25 | 20 | 18,18 | 16,67 | 10 | 1 |
Zie afbeelding (rode grafiek)
c. Zie het gedeelte van de rode grafiek tussen de stippellijntjes.

3.
a.
Entree is 15 euro.
b.
| a | 10 | 20 | 30 | 40 | 50 | 55 | 60 | 100 | 1000 |
| B | 115 | 65 | 48,33 | 40 | 35 | 33,18 | 31,67 | 25 | 16 |
Zie afbeelding (groene grafiek): bij 30 euro hoort 67 leerlingen.
d. B = (1000 / 51) + 15 = 34,61 euro
4.
Tip:
Hoe meer wachtenden, hoe korter de schommeltijd. Dus hoe groter a wordt, des te kleiner wordt de schommeltijd.
Er kunnen geen 0 wachtenden zijn want 360 / 0 dat kan niet!
a.Hoe meer wachtenden, hoe korter de schommeltijd. Dus hoe groter a wordt, des te kleiner wordt de schommeltijd.
Er kunnen geen 0 wachtenden zijn want 360 / 0 dat kan niet!
| aantal wachtenden | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 240 | 360 |
| schommel minuten | 36 | 18 | 12 | 9 | 7,2 | 6 | 5,1 | 4,5 | 4 | 3,6 | 1,5 | 1 |
Bij a = 20 krijgen we: schommeltijd = 360 / 20 = 18 minuten
c.
Bij a = 240 krijgen we: schommeltijd = 360 / 240 = 1,5 minuut

5.
Tip:
Zie het 1e groene punt:
Hoeveel wachtenden heb je bij 3 schommelminuten?
Voor welke a geldt: 360 / a = 3? Dat is bij a = 120.
a. Zie grafiek opgave 4: dat is het gedeelte van de grafiek tussen de 2 groene pijltjes.Zie het 1e groene punt:
Hoeveel wachtenden heb je bij 3 schommelminuten?
Voor welke a geldt: 360 / a = 3? Dat is bij a = 120.
b. Bij a = 360 krijgen we: schommeltijd = 360 / 360 = 1 minuut
c. *
6.
Tip:
Als B = 24 / a <=> B x a = 24
Zie: 3 = 6 / 2 <=> 3 x 2 = 6
a.Als B = 24 / a <=> B x a = 24
Zie: 3 = 6 / 2 <=> 3 x 2 = 6
| a | 1 | 2 | 3 | 4 | 6 | 9 | 12 | 18 | 36 |
| P | 36 | 18 | 12 | 9 | 6 | 4 | 3 | 2 | 1 |
| a | 1 | 2 | 3 | 4 | 6 | 9 | 12 | 18 | 36 |
| P | 36 | 18 | 12 | 9 | 6 | 4 | 3 | 2 | 1 |
Ze zijn gelijk.
7.
Tip:
a x B = 50
deel nu links en rechts daar 'a' volgens de balansmethode
Dan volgt hieruit: B = 50 / a
a. a x B = 50
deel nu links en rechts daar 'a' volgens de balansmethode
Dan volgt hieruit: B = 50 / a
10 x B = 50 => B = 5
Dus bedrag per persoon is €5,=.
b.
| a | 1 | 2 | 5 | 10 | 25 | 50 |
| B | 50 | 25 | 10 | 5 | 2 | 1 |
d. B = 50 / a

8.
Tip:
Gebruik de formule en vul in wat je weet.
a. Gebruik de formule en vul in wat je weet.
a x G = 2400
12 x G = 2400
G = 2400 / 12 = 200 gram
b.
a x G = 2400
a x 600 = 2400
a = 2400 / 600
a = 4 personen
c.
G = 2400 / a (links en rechts delen door 'a')
9.
Tip:
Als je de bovenste rij x5 doet, dan is dat ook zo bij de onderste rij. Dus het is een evenredig verband. En een evenredig verband is een rechte lijn.
a. 1 hamburger kost: 12,50 / 5 = 2,50 euroAls je de bovenste rij x5 doet, dan is dat ook zo bij de onderste rij. Dus het is een evenredig verband. En een evenredig verband is een rechte lijn.
b.
| aantal hamburgers | 1 | 5 | 10 | 20 | 30 |
| prijs in euro | 2,50 | 12,50 | 25 | 50 | 75 |
d. Als je 4x zoveel hamburgers koopt, moet je ook 4x zoveel betalen.
e. Zie afbeelding

10.
Tip:
Omgekeerd evenredig: Als de ene variabele 5x zo groot wordt, dan wordt de andere variabele 5x zo klein.
Evenredig: Als de ene variabele 5x zo groot wordt, dan wordt de andere variabele ook 5x zo groot.
a. Als p 2x zo groot wordt (zie 4 -> 8) dan wordt T 2x zo klein (zie 18 -> 9).Omgekeerd evenredig: Als de ene variabele 5x zo groot wordt, dan wordt de andere variabele 5x zo klein.
Evenredig: Als de ene variabele 5x zo groot wordt, dan wordt de andere variabele ook 5x zo groot.
Dus er is sprake van een omgekeerd evenredig verband.
b. Als a 3x zo groot wordt (zie 3 -> 9) dan wordt N ook 3x zo groot (8 -> 24).
Dus er is sprake van een evenredig verband.
c. Bij tabel I hoort een hyperbool, bij tabel II hoort een rechte lijn.
d. Tabel I:
| p | 3 | 4 | 8 | 9 | 36 |
| T | 24 | 18 | 9 | 8 | 2 |
Tabel II:
| a | 3 | 9 | 12 | 24 | 60 |
| N | 8 | 24 | 32 | 64 | 160 |
11.
Dus er is sprake van een omgekeerd evenredig verband.
b. Alle roosterpunten kloppen bij: G = 240 / Z en Z x G = 240
12.
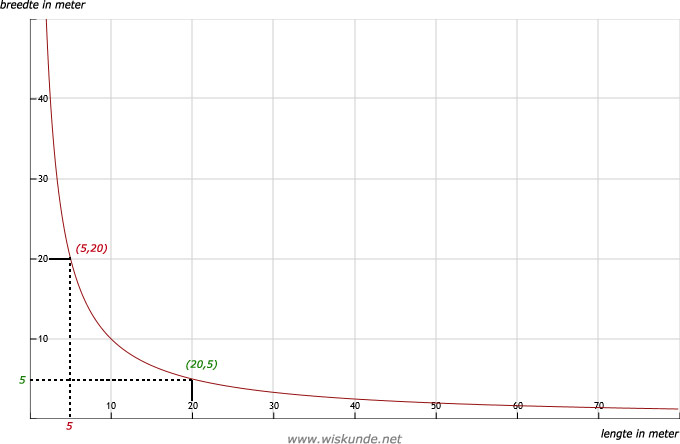
b. Als de lengte 12,5 m is, dan is de breedte 8 m. Want: oppervlakte = 12,5 x 8 = 100
c.
d. Als de lengte 5x zo groot wordt (zie 5 -> 25) dan wordt de breedte 5x zo klein (zie 20 -> 4).
Dus er is sprake van een omgekeerd evenredig verband.
13.
b. Zie afbeelding
c. Een plaats moet minimaal 5 meter hebben. Anders past er geen auto op. Dus de rode boog tussen (5,20) en (20,5) is zinvol.
14.
Dus: h = 120/12 = 10. Dus de hoogte van de doos is dan 10 dm.
b. Omgekeerd evenredig, want hoe groter het grondvlak G wordt, des te kleiner wordt de hoogte h.
c. Bij de verticale as komt h te staan. Dus op de horizontale as komt G te staan.
d.
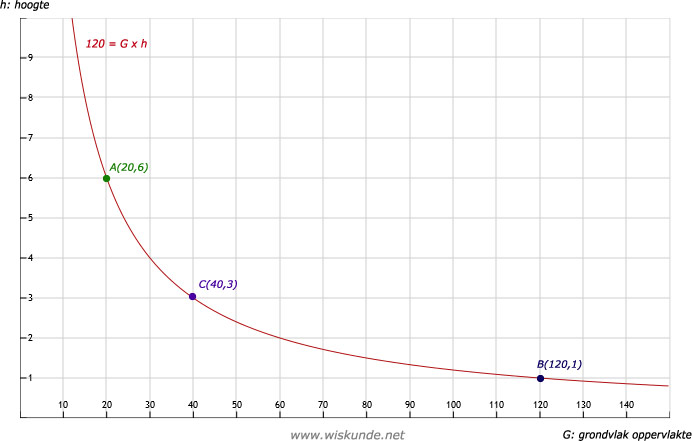
15.
Doos A: Als h = 6 dan G = 20. Dus coördinaat A(20,6).
Doos B: Als h = 1 dan G = 120. Dus coördinaat B(120,1).
Doos C: Als G = 40 dan h = 3. Dus coördinaat C(40,3).
Tip:
Bij b: Vul de roosterpunten in de formule(s) en kijk voor welke het klopt.
Roosterpunten zijn van de vorm: (G,Z). Bijvoorbeeld (2,120) en (3,80) en (6,40) enz.
a. Als G 2x zo groot wordt (zie 2 -> 4) dan wordt Z 2x zo klein (zie 120 -> 60).Bij b: Vul de roosterpunten in de formule(s) en kijk voor welke het klopt.
Roosterpunten zijn van de vorm: (G,Z). Bijvoorbeeld (2,120) en (3,80) en (6,40) enz.
Dus er is sprake van een omgekeerd evenredig verband.
b. Alle roosterpunten kloppen bij: G = 240 / Z en Z x G = 240
12.
Tip:
Je kan ook zeggen bij omgekeerd evenredig:
De bovenste rij x 2 dan de onderste rij x 1/2. En 1/2 is het omgekeerde van 2.
a. Als de lengte 20 m is, dan is de breedte 5 m. Want: oppervlakte = 20 x 5 = 100Je kan ook zeggen bij omgekeerd evenredig:
De bovenste rij x 2 dan de onderste rij x 1/2. En 1/2 is het omgekeerde van 2.
b. Als de lengte 12,5 m is, dan is de breedte 8 m. Want: oppervlakte = 12,5 x 8 = 100
c.
| l | 1 | 2 | 4 | 5 | 8 | 10 | 12,5 | 20 | 25 | 50 | 100 |
| b | 100 | 50 | 25 | 20 | 12,5 | 10 | 8 | 5 | 4 | 2 | 1 |
Dus er is sprake van een omgekeerd evenredig verband.
13.
Tip:
5x zo klein betekent: x1/5
a. l x b = 1005x zo klein betekent: x1/5
b. Zie afbeelding
c. Een plaats moet minimaal 5 meter hebben. Anders past er geen auto op. Dus de rode boog tussen (5,20) en (20,5) is zinvol.

14.
Tip:
Inhoud = G x h, de inhoud ligt vast, want die is steeds 120, dus als G stijgt, moet h wel dalen in de formule.
Anders is het links en rechts van het =-teken niet gelijk. En andersom geldt natuurlijk hetzelfde.
a. 12 x h = 120Inhoud = G x h, de inhoud ligt vast, want die is steeds 120, dus als G stijgt, moet h wel dalen in de formule.
Anders is het links en rechts van het =-teken niet gelijk. En andersom geldt natuurlijk hetzelfde.
Dus: h = 120/12 = 10. Dus de hoogte van de doos is dan 10 dm.
b. Omgekeerd evenredig, want hoe groter het grondvlak G wordt, des te kleiner wordt de hoogte h.
c. Bij de verticale as komt h te staan. Dus op de horizontale as komt G te staan.
d.
| Grondvlak G | 10 | 20 | 30 | 40 | 60 | 80 | 100 | 120 |
| Hoogte h | 12 | 6 | 4 | 3 | 2 | 1,5 | 1,2 | 1 |

15.
Tip:
In plaats van de gebruikelijke (x,y) hebben we nu (G,h) als coördinaten.
Zie de afbeelding bij opgave 14.In plaats van de gebruikelijke (x,y) hebben we nu (G,h) als coördinaten.
Doos A: Als h = 6 dan G = 20. Dus coördinaat A(20,6).
Doos B: Als h = 1 dan G = 120. Dus coördinaat B(120,1).
Doos C: Als G = 40 dan h = 3. Dus coördinaat C(40,3).
Andere paragrafen:
3.1. Evenredig en omgekeerd evenredig (1 t/m 15)
3.2. Allerlei formules en grafieken (16 t/m 27)
3.3. Gelijkwaardige formules (28 t/m 41)
3.4. Vergelijkingen oplossen (42 t/m 58)
3.6. Gemengde opgaven (79 t/m 90)
3.1. Evenredig en omgekeerd evenredig (1 t/m 15)
3.2. Allerlei formules en grafieken (16 t/m 27)
3.3. Gelijkwaardige formules (28 t/m 41)
3.4. Vergelijkingen oplossen (42 t/m 58)
3.6. Gemengde opgaven (79 t/m 90)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


