TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 3.3 Gelijkwaardige formules VMBO 4 KGT
Boek: Getal & Ruimte - Verbanden 2 VMBO 4 (deel 1) opgaven 28 t/m 41, 2011Wat zijn gelijkwaardige formules?
Formules zijn gelijkwaardig als de uitkomsten van beide formules hetzelfde zijn bij dezelfde input.
Dus als je 5 getallenparen hebt die horen bij de ene formule en deze horen ook bij de andere formule dan zijn ze gelijkwaardig.
Vaak zie je bij gelijkwaardige formules dat je bij de ene formule de ene variabele vrijschrijft en bij de andere formule de andere variabele vrijschrijft.
Je kunt ook eenvoudig zeggen dat de grafieken van deze formules samenvallen.
Formules zijn gelijkwaardig als de uitkomsten van beide formules hetzelfde zijn bij dezelfde input.
Dus als je 5 getallenparen hebt die horen bij de ene formule en deze horen ook bij de andere formule dan zijn ze gelijkwaardig.
Vaak zie je bij gelijkwaardige formules dat je bij de ene formule de ene variabele vrijschrijft en bij de andere formule de andere variabele vrijschrijft.
Je kunt ook eenvoudig zeggen dat de grafieken van deze formules samenvallen.
28.
a. Het startgeld is €5,-. Per rondje is het €0,50.
b. opbrengst in euro = 5 + 0,5 x 30 = 20. Dus het is 20 euro.
c. a = (20 - 5) / 0,5 = 15/0,5 = 30. Hij moet dus 30 rondjes lopen om 20,- op te halen.
d. Bij beide formules is de opbrengst 20,= als je 30 rondjes loopt.
29.
Vul nu opbrengst = 10 in de 2e formule:
=> a = 2 x 10 - 10 = 10
Dus het klopt!
Kies a = 20 en dan wordt de opbrengst: 5 + 0,5 x 20 = 15
Vul nu opbrengst = 15 in de 2e formule:
=> a = 2 x 15 - 10 = 20
Dus het klopt!
Dus de twee formules zijn gelijkwaardig.
30.
b. opbrengst in euro = 3 + 0,5 x 30 = 18. Dus 18 euro.
c. a = 2 x opbrengst in euro - 6
d. opbrengst = 3 + 0,5a
20 = 3 + 0,5a
0,5a = 17
a = 34
Dus hij moet 34 rondjes lopen om €20,- op te halen.
31.
32.
Bekijk de tabel van opgave 31. Daar is de tabel wat meer uitgeschreven. Je ziet dat bij rangnummer 17 je een lengte van de ribbe krijgt van 35. Dus de toren bestaat dan uit 17 blokjes.
33.
lengte ribbe = 2 x rangnummer + 1
in het kort: l = 2n + 1
34.
35.
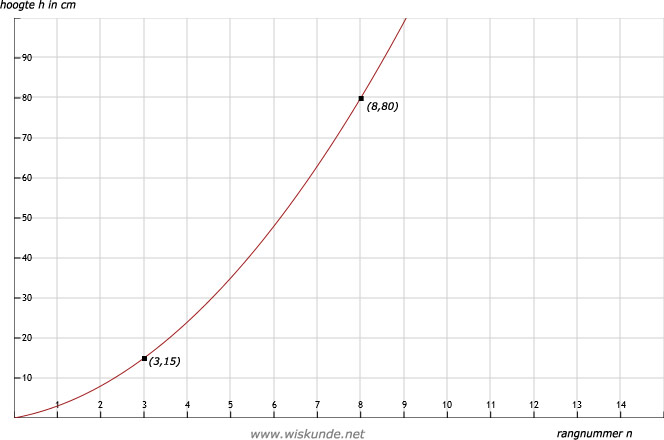
Zie afbeelding
36.
Kies n = 15 dan h = 152 + 2 x 15 = 255 cm. Dat is nog net te hoog.
Kies n = 14 dan h = 142 + 2 x 14 = 224 cm. Dat past in zijn kamer.
Dus: hij kan maximaal 14 blokken stapelen. Deze geeft een hoogte van 224 cm.
37.
2e formule: h = n(n + 2) = n x n + 2 x n = n2 + 2n
Je ziet nu dat de 1e en 2e formule precies gelijk zijn. Dus ze zijn gelijkwaardig.
a. Het startgeld is €5,-. Per rondje is het €0,50.
b. opbrengst in euro = 5 + 0,5 x 30 = 20. Dus het is 20 euro.
c. a = (20 - 5) / 0,5 = 15/0,5 = 30. Hij moet dus 30 rondjes lopen om 20,- op te halen.
d. Bij beide formules is de opbrengst 20,= als je 30 rondjes loopt.
29.
Tip:
Kies 2 getallenparen en kijk of het bij beide formules klopt.
Kies a = 10 en dan wordt de opbrengst: 5 + 0,5 x 10 = 10Kies 2 getallenparen en kijk of het bij beide formules klopt.
Vul nu opbrengst = 10 in de 2e formule:
=> a = 2 x 10 - 10 = 10
Dus het klopt!
Kies a = 20 en dan wordt de opbrengst: 5 + 0,5 x 20 = 15
Vul nu opbrengst = 15 in de 2e formule:
=> a = 2 x 15 - 10 = 20
Dus het klopt!
Dus de twee formules zijn gelijkwaardig.
30.
Tip:
Bij c. kun je bij de 1e formule ook de 'a=' vrijschrijven met de balansmethode. Kies anders 2 getallenparen.
a. opbrengst in euro = 3 + 0,5aBij c. kun je bij de 1e formule ook de 'a=' vrijschrijven met de balansmethode. Kies anders 2 getallenparen.
b. opbrengst in euro = 3 + 0,5 x 30 = 18. Dus 18 euro.
c. a = 2 x opbrengst in euro - 6
d. opbrengst = 3 + 0,5a
20 = 3 + 0,5a
0,5a = 17
a = 34
Dus hij moet 34 rondjes lopen om €20,- op te halen.
31.
Tip:
lengte ribbe is (getal bovenste rij maal 2) en dan 1 erbij
lengte ribbe is (getal bovenste rij maal 2) en dan 1 erbij
| rangnumer n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| lengte ribbe in cm | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 | 29 | 31 | 33 | 35 |
32.
Bekijk de tabel van opgave 31. Daar is de tabel wat meer uitgeschreven. Je ziet dat bij rangnummer 17 je een lengte van de ribbe krijgt van 35. Dus de toren bestaat dan uit 17 blokjes.
33.
Tip:
De formule is 2x het rangnummer en dan nog 1 erbij.
De formule wordt: De formule is 2x het rangnummer en dan nog 1 erbij.
lengte ribbe = 2 x rangnummer + 1
in het kort: l = 2n + 1
34.
Tip:
Neem n = 5 dan h = 52 + 2 x 5 = 25 + 10 = 35
Neem n = 5 dan h = 52 + 2 x 5 = 25 + 10 = 35
| rangnummer n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| hoogte h in cm | 3 | 8 | 15 | 24 | 35 | 48 | 63 | 80 | 99 | 120 |
35.
Zie afbeelding

36.
Tip:
Maak gebruik van inklemmen. Start bijvoorbeeld met n = 20.
Kies n = 20 dan h = 202 + 2 x 20 = 440 cm. Dat is dus te hoog.Maak gebruik van inklemmen. Start bijvoorbeeld met n = 20.
Kies n = 15 dan h = 152 + 2 x 15 = 255 cm. Dat is nog net te hoog.
Kies n = 14 dan h = 142 + 2 x 14 = 224 cm. Dat past in zijn kamer.
Dus: hij kan maximaal 14 blokken stapelen. Deze geeft een hoogte van 224 cm.
37.
Tip:
Werk de haakjes weg en kijk of de formules gelijkwaardig zijn. Of zoek 2 getallenparen.
Werk de haakjes weg bij de 2e formule. Je krijgt dan:Werk de haakjes weg en kijk of de formules gelijkwaardig zijn. Of zoek 2 getallenparen.
2e formule: h = n(n + 2) = n x n + 2 x n = n2 + 2n
Je ziet nu dat de 1e en 2e formule precies gelijk zijn. Dus ze zijn gelijkwaardig.
38.
p = 1000 - 4 x 73 = 708. Dus 708 punten na 73 fouten.
b.
p = 1000 - 4f
-4f = p - 1000
f = (p - 1000) / -4 = p/-4 + -1000/-4 = p/-4 + 250 = 250 - p/4
Dus: f = 250 - p/4
c.
f = 250 - p/4 vul in wat je weet:
f = 250 - 596/4
f = 250 - 149
f = 101
Dus 101 fouten
39.
Dus bij 12 rijen zijn er meer dan 50 zitplaatsen.
40.
totaal aantal zitplaatsen = 1,5 x 72 + 14,5 x 7 = 175
Dus het totaal aantal zitplaatsen is 175.
41.
totaal aantal zitplaatsen = 0,5n x 3n + 0,5n x 28 = 1,5n2 + 14n.
Je ziet een verschil van 0,5n met de 1e formule. Dus ze zijn niet gelijkwaardig.
Tevens: (7,175) is wel een oplossing van de 1e formule maar niet voor de formule van Joris.
Tip:
Bij b: schrijf f vrij door gebruik te maken van de balansmethode. Of zoek 2 getallenparen.
a.Bij b: schrijf f vrij door gebruik te maken van de balansmethode. Of zoek 2 getallenparen.
p = 1000 - 4 x 73 = 708. Dus 708 punten na 73 fouten.
b.
p = 1000 - 4f
-4f = p - 1000
f = (p - 1000) / -4 = p/-4 + -1000/-4 = p/-4 + 250 = 250 - p/4
Dus: f = 250 - p/4
c.
f = 250 - p/4 vul in wat je weet:
f = 250 - 596/4
f = 250 - 149
f = 101
Dus 101 fouten
39.
Tip:
Maak een tabel en kijk wanneer je voorbij de 50 komt.
Maak een tabel en kijk wanneer je voorbij de 50 komt.
| rijnummer | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| aantal zitplaatsen | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 |
Dus bij 12 rijen zijn er meer dan 50 zitplaatsen.
40.
Tip:
Vul in n = 7 in de formule en je krijgt het aantal zitplaatsen van rij 1 t/m rij 7.
n = 7 levert:Vul in n = 7 in de formule en je krijgt het aantal zitplaatsen van rij 1 t/m rij 7.
totaal aantal zitplaatsen = 1,5 x 72 + 14,5 x 7 = 175
Dus het totaal aantal zitplaatsen is 175.
41.
Tip:
Werk de haakjes weg van de nieuwe formule. Of neem een getallenpaar en zie dat het niet klopt bij beide formules.
De formule van Joris wordt als je de haakjes wegwerkt:Werk de haakjes weg van de nieuwe formule. Of neem een getallenpaar en zie dat het niet klopt bij beide formules.
totaal aantal zitplaatsen = 0,5n x 3n + 0,5n x 28 = 1,5n2 + 14n.
Je ziet een verschil van 0,5n met de 1e formule. Dus ze zijn niet gelijkwaardig.
Tevens: (7,175) is wel een oplossing van de 1e formule maar niet voor de formule van Joris.
Andere paragrafen:
3.1. Evenredig en omgekeerd evenredig (1 t/m 15)
3.2. Allerlei formules en grafieken (16 t/m 27)
3.3. Gelijkwaardige formules (28 t/m 41)
3.4. Vergelijkingen oplossen (42 t/m 58)
3.6. Gemengde opgaven (79 t/m 90)
3.1. Evenredig en omgekeerd evenredig (1 t/m 15)
3.2. Allerlei formules en grafieken (16 t/m 27)
3.3. Gelijkwaardige formules (28 t/m 41)
3.4. Vergelijkingen oplossen (42 t/m 58)
3.6. Gemengde opgaven (79 t/m 90)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


