TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 3.2 Allerlei formules en grafieken VMBO 4 KGT
Boek: Getal & Ruimte - Verbanden 2 VMBO 4 (deel 1) opgaven 16 t/m 27, 2011Een paar bijzondere grafieken:
Trapjesgrafiek: is een grafiek die bestaat uit horizontale lijntjes. Je krijgt die horizontale lijntjes omdat de tussenliggende waarden geen betekenis hebben.
Stippengrafiek: is een grafiek waarbij je bij elke waarneming een stip zet. Hoe meer stippen je zet, hoe beter het beeld van de grafiek. Bij een stippengrafiek zou je mogelijk een vloeiende kromme kunnen tekenen.
Trapjesgrafiek: is een grafiek die bestaat uit horizontale lijntjes. Je krijgt die horizontale lijntjes omdat de tussenliggende waarden geen betekenis hebben.
Stippengrafiek: is een grafiek waarbij je bij elke waarneming een stip zet. Hoe meer stippen je zet, hoe beter het beeld van de grafiek. Bij een stippengrafiek zou je mogelijk een vloeiende kromme kunnen tekenen.
16.
17.
b. t = 120 in 2020: de gemiddelde lengte was in 2020: 1785 mm. Ofwel 1 meter en 78 cm en 5 mm.
18.
t = -600 in 1300
t = -604 in 1296
Dus de t die erbij hoort, is t = -604.
b. lengte in mm = 1630 + 1,25 x -604 = 875 mm. Dat is 87,5 cm.
c. Een lengte van 87,5 cm is aan de lage kant voor een persoon. Maar dat komt omdat de formule niet voor alle tijden geldt.
Een groeiformule voor personen voor een periode van 700 jaar is niet realistisch. Zo'n formule zou wel kunnen voor bijvoorbeeld 25-50 jaar.
19.
b. 5,2 / 40 = 0,13 jaar
c. levensverwachting voor de vrouw = 75,4 + 0,13t
d. Bij 2050 hoort t = 90
levensverwachting voor de vrouw = 75,4 + 0,13 x 90 = 87,1 jaar
20.
b. De levensverwachting voor de man in 2050 (t=90) = 70 + 0,16 x 90 = 84,4 jaar.
De levensverwachting voor de vrouw in 2050 (t=90) = 75,4 + 0,13 x 90 = 87,1 jaar.
Dus in 2050 wordt een vrouw gemiddeld 2,7 jaar ouder dan een man.
21.
Levensverwachtingen in 1296 vrouw: 75,4 + 0,13 x -664 = -10,92 jaar
Je krijgt negatieve levensverwachtingen in 1296. Dat kan natuurlijk niet.
22.
b. k = B / 2 = 103 / 2 = 51,5, dus zijn kledingmaat wordt 52.
c. k = B / 2 = 105 / 2 = 52,5, dus zijn kledingmaat wordt 54.
d. 54 = B / 2 => B = 54 x 2 = 108
Andere mogelijkheden zijn: 105, 106, 107 en 108.
Je zag bij c. dat een borstomvang van 105 ook een kledingmaat van 54 geeft. Dus de waarden tussen 105 en 108 ook.
23.
24.
a.
b.
Zie afbeelding
25.
Zie afbeelding
| Verband | Letter |
| kwadratisch verband | (v) |
| wortel verband | (e) |
| dalend lineair verband | (r) |
| exponentieel verband | (b) |
| machts verband | (a) |
| evenredig verband | (n) |
| periodiek verband | (d) |
| stijgend lineair verband | (e) |
| omgekeerd evenredig verband | (n) |
17.
Tip:
Als t = 0 in 1900 dan:
t = 20 in 1920
t = 100 in 2000
a. t = 100 in 2000: de gemiddelde lengte was in 2000: 1750 mm. Ofwel 1 meter en 75 cm.Als t = 0 in 1900 dan:
t = 20 in 1920
t = 100 in 2000
b. t = 120 in 2020: de gemiddelde lengte was in 2020: 1785 mm. Ofwel 1 meter en 78 cm en 5 mm.
18.
Tip:
Als t = 0 in 1900 dan:
t = -100 in 1800
a. Als t = 0 in 1900 dan:Als t = 0 in 1900 dan:
t = -100 in 1800
t = -600 in 1300
t = -604 in 1296
Dus de t die erbij hoort, is t = -604.
b. lengte in mm = 1630 + 1,25 x -604 = 875 mm. Dat is 87,5 cm.
c. Een lengte van 87,5 cm is aan de lage kant voor een persoon. Maar dat komt omdat de formule niet voor alle tijden geldt.
Een groeiformule voor personen voor een periode van 700 jaar is niet realistisch. Zo'n formule zou wel kunnen voor bijvoorbeeld 25-50 jaar.
19.
Tip:
De beginwaarde die hoort bij t = 0 is bij het jaar 1960. Dus de beginwaarde is 75,4.
Dus t = 1 is het jaar 1961 (1960 + 1).
Dus t = 90 is het jaar 2050 (1960 + 90).
a. De levensverwachting is met 80,6 - 75,4 = 5,2 jaar gestegen in 40 jaar tijd.De beginwaarde die hoort bij t = 0 is bij het jaar 1960. Dus de beginwaarde is 75,4.
Dus t = 1 is het jaar 1961 (1960 + 1).
Dus t = 90 is het jaar 2050 (1960 + 90).
b. 5,2 / 40 = 0,13 jaar
c. levensverwachting voor de vrouw = 75,4 + 0,13t
d. Bij 2050 hoort t = 90
levensverwachting voor de vrouw = 75,4 + 0,13 x 90 = 87,1 jaar
20.
Tip:
Bij 1960 hoort t = 0.
a. De levensverwachting voor de man in 1960 (t=0) = 70 + 0,16 x 0 = 70 jaar.Bij 1960 hoort t = 0.
b. De levensverwachting voor de man in 2050 (t=90) = 70 + 0,16 x 90 = 84,4 jaar.
De levensverwachting voor de vrouw in 2050 (t=90) = 75,4 + 0,13 x 90 = 87,1 jaar.
Dus in 2050 wordt een vrouw gemiddeld 2,7 jaar ouder dan een man.
21.
Tip:
Bij t = 0 hoort 1960
Bij t = -700 hoort 1260
Bij t = -664 hoort 1296 (het jaar van Floris V)
Levensverwachtingen in 1296 man: 70 + 0,16 x -664 = -36,24 jaarBij t = 0 hoort 1960
Bij t = -700 hoort 1260
Bij t = -664 hoort 1296 (het jaar van Floris V)
Levensverwachtingen in 1296 vrouw: 75,4 + 0,13 x -664 = -10,92 jaar
Je krijgt negatieve levensverwachtingen in 1296. Dat kan natuurlijk niet.
22.
Tip:
Maak formule:
kledingmaat = Borstomvang / 2
In het kort: k = B / 2
a. k = B / 2 = 102 / 2 = 51, dus zijn kledingmaat wordt 52.Maak formule:
kledingmaat = Borstomvang / 2
In het kort: k = B / 2
b. k = B / 2 = 103 / 2 = 51,5, dus zijn kledingmaat wordt 52.
c. k = B / 2 = 105 / 2 = 52,5, dus zijn kledingmaat wordt 54.
d. 54 = B / 2 => B = 54 x 2 = 108
Andere mogelijkheden zijn: 105, 106, 107 en 108.
Je zag bij c. dat een borstomvang van 105 ook een kledingmaat van 54 geeft. Dus de waarden tussen 105 en 108 ook.
23.
| Borstomvang | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 |
| maat | 48 | 48 | 48 | 48 | 50 | 50 | 50 | 50 | 52 | 52 | 52 |
| Borstomvang | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 |
| maat | 52 | 54 | 54 | 54 | 54 | 56 | 56 | 56 | 56 | 58 |
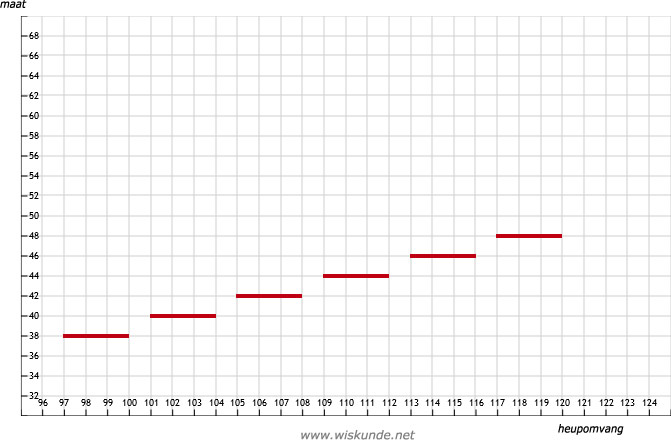
24.
a.
| Heupomvang | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 |
| maat | 36 | 38 | 38 | 38 | 38 | 40 | 40 | 40 | 40 | 42 | 42 | 42 | 42 |
| Heupomvang | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 |
| maat | 44 | 44 | 44 | 44 | 46 | 46 | 46 | 46 | 48 | 48 | 48 | 48 |
b.
Zie afbeelding

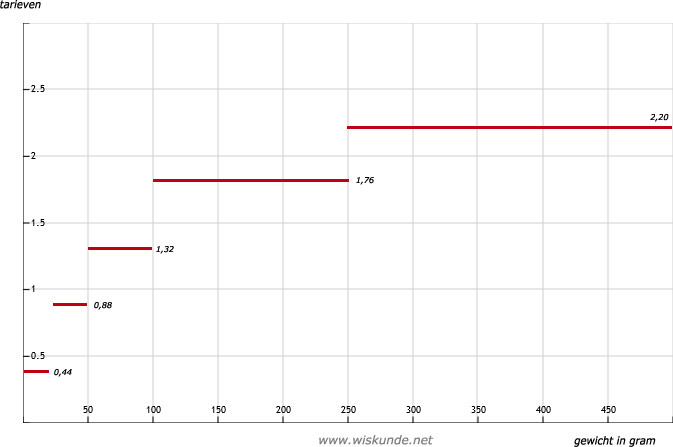
25.
Zie afbeelding

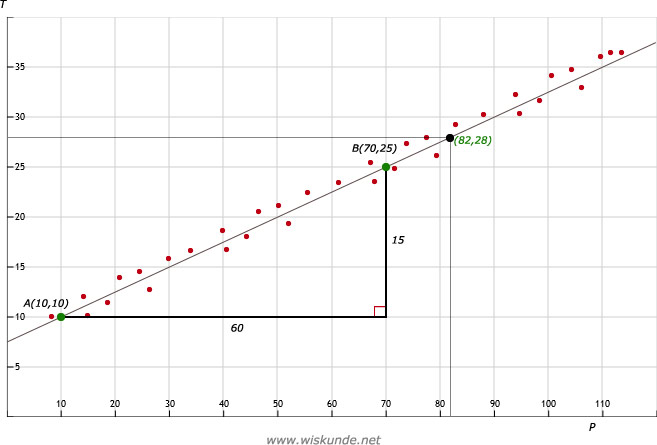
26.
b. Zie afbeelding
c. Stapgrootte = toename verticaal / toename horizontaal = 15 / 60 = 1/4
Begingetal is snijpunt met de verticale as (T-as): 7,5
De formule wordt dus: T = 7,5 + 1/4P
27.
a. T = 7,5 + 1/4P
T = 7,5 + 1/4 x 82
T = 28
Dus T is 28º.
b. Zie afbeelding opgave 26. Zie punt (zwart/groen): (82,28).
Tip:
Bepaal de stapgrootte met de punten A en B.
a. minderBepaal de stapgrootte met de punten A en B.
b. Zie afbeelding
c. Stapgrootte = toename verticaal / toename horizontaal = 15 / 60 = 1/4
Begingetal is snijpunt met de verticale as (T-as): 7,5
De formule wordt dus: T = 7,5 + 1/4P

27.
a. T = 7,5 + 1/4P
T = 7,5 + 1/4 x 82
T = 28
Dus T is 28º.
b. Zie afbeelding opgave 26. Zie punt (zwart/groen): (82,28).
Andere paragrafen:
3.1. Evenredig en omgekeerd evenredig (1 t/m 15)
3.2. Allerlei formules en grafieken (16 t/m 27)
3.3. Gelijkwaardige formules (28 t/m 41)
3.4. Vergelijkingen oplossen (42 t/m 58)
3.6. Gemengde opgaven (79 t/m 90)
3.1. Evenredig en omgekeerd evenredig (1 t/m 15)
3.2. Allerlei formules en grafieken (16 t/m 27)
3.3. Gelijkwaardige formules (28 t/m 41)
3.4. Vergelijkingen oplossen (42 t/m 58)
3.6. Gemengde opgaven (79 t/m 90)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


