TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 1.3 Lineaire formules VWO 3
Boek: Getal & Ruimte - Lineaire problemen VWO 3 (deel 1) opgaven 30 t/m 49, 2011Wat is een lineaire formule?
Een lineaire formule is een rechte lijn en deze is van de vorm y = ax + b. De richtingscoëfficient is het getal dat voor de x staat.
In de algemene formulering is dat dus 'a'. Het snijpunt met de y-as krijgen we door x = 0 in te vullen in de formule. Snijpunt y-as is dus (0,b). Een voorbeeld van een lineaire formule is y = 4x - 3.
In dit voorbeeld is de richtingscoëfficient dus gelijk aan 4 en het snijpunt met de y-as: (0,-3).
We noteren dat ook wel als rclijn = 4. Om de grafiek te tekenen, beginnen we bij (0,-3) en gaan daarna 1 naar rechts en 4 omhoog.
Om te controleren of het punt A(1,1) op de lijn ligt, vul je dit punt in de formule en kijk of de vergelijking klopt.
Een lineaire formule is een rechte lijn en deze is van de vorm y = ax + b. De richtingscoëfficient is het getal dat voor de x staat.
In de algemene formulering is dat dus 'a'. Het snijpunt met de y-as krijgen we door x = 0 in te vullen in de formule. Snijpunt y-as is dus (0,b). Een voorbeeld van een lineaire formule is y = 4x - 3.
In dit voorbeeld is de richtingscoëfficient dus gelijk aan 4 en het snijpunt met de y-as: (0,-3).
We noteren dat ook wel als rclijn = 4. Om de grafiek te tekenen, beginnen we bij (0,-3) en gaan daarna 1 naar rechts en 4 omhoog.
Om te controleren of het punt A(1,1) op de lijn ligt, vul je dit punt in de formule en kijk of de vergelijking klopt.
30.
b. Bij x = 0 hoort y = 3
c. De 3 in de formule geeft het snijpunt met de y-as: (0,3)
d. -1/2 is de richtingscoëfficient. Het betekent: 1 naar rechts en dan 1/2 omlaag.
e. y = 2x + 1
31.
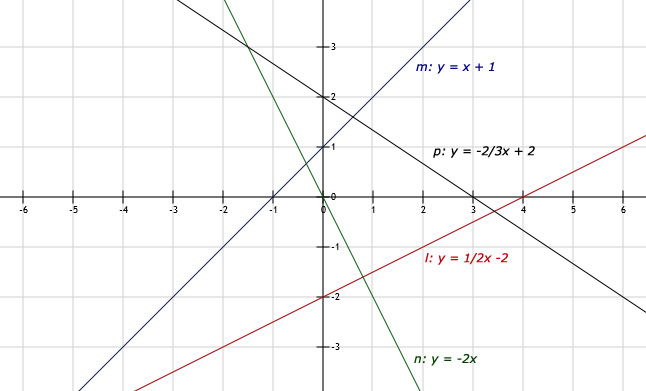
Zie afbeelding
32.
33.
a. Vul in x = 7. Dit levert y = 56 - 13 = 43. Dus het punt P(7,43) ligt op de lijn l:.
b. Vul in x = 10. Dit levert y = 80 - 13 = 67. Dus het punt P(10,93) ligt niet op de lijn. Maar punt (10,67) dus wel.
c. Vul in x = -4. Dit levert y = -45. Dus het punt A(-4,-45) ligt op de lijn.
d. Vul B(20,p) in l: levert: p = 8 x 20 - 13 = 147. Dus p = 147.
34.
a. a = 64
b. b = 1/7
c. c = 1
35.
a. Achtlo hoort bij N = 30t + 1800. Want 1800 is het snijpunt met de y-as bij t = 0.
b. Los op: 18t + 2100 = 30t + 1800, levert t = 25.
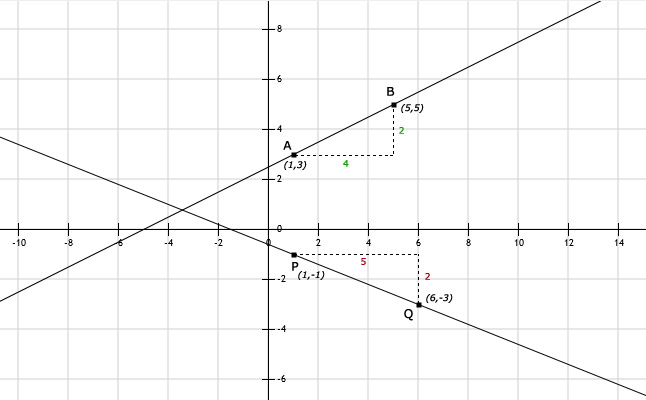
c. 18t + 2100 + 30t + 1800 = 5000 levert bij t = 1100/48 ≈ 22,91.
36.
a. Omdat er ieder jaar steeds een gelijke daling is van 3000 bedrijven.
b. Aantal bedrijven op 1 januari zou kunnen zijn: 92 + 3 + 3 -> 98 000
c. 3 000
d. N = -3t + 98
e. *
37.
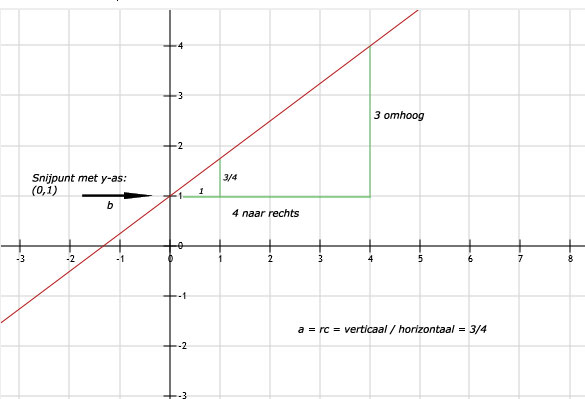
a. Snijpunt met de y-as is (0,1). Dus b = 1.
b. De grafiek gaat 4 naar rechts en 3 omhoog. Ofwel 1 naar rechts en 3/4 omhoog.
c. Dus a = 3/4.
d. De formule van deze lijn wordt dan: y = 3/4x + 1
38.
De formule van lijn l: is: y = x + 2
De formule van lijn m: is: y = -1½x + 1
De formule van lijn n: is: y = -1/3x + 4
b. De formule van lijn k: is: y = -1/3x - 3
39.
De formule van lijn q: is: y = ½x - 1½
De formule van lijn r: is: y = -2x
Tip:
Snijpunt met de y-as? Dan is x = 0. Snijpunt met de x-as? Dan y = 0.
Bedenk: -1/2 omhoog is hetzelfde als 1/2 omlaag!
a. Bij x = 2 hoort y = 2Snijpunt met de y-as? Dan is x = 0. Snijpunt met de x-as? Dan y = 0.
Bedenk: -1/2 omhoog is hetzelfde als 1/2 omlaag!
b. Bij x = 0 hoort y = 3
c. De 3 in de formule geeft het snijpunt met de y-as: (0,3)
d. -1/2 is de richtingscoëfficient. Het betekent: 1 naar rechts en dan 1/2 omlaag.
e. y = 2x + 1
31.
Zie afbeelding

32.
Tip:
Om een lijn te tekenen, heb je maar 2 punten nodig. Neem dan 2 makkelijke punten. Bijvoorbeeld de snijpunten met de x-as (0,b) en y-as.
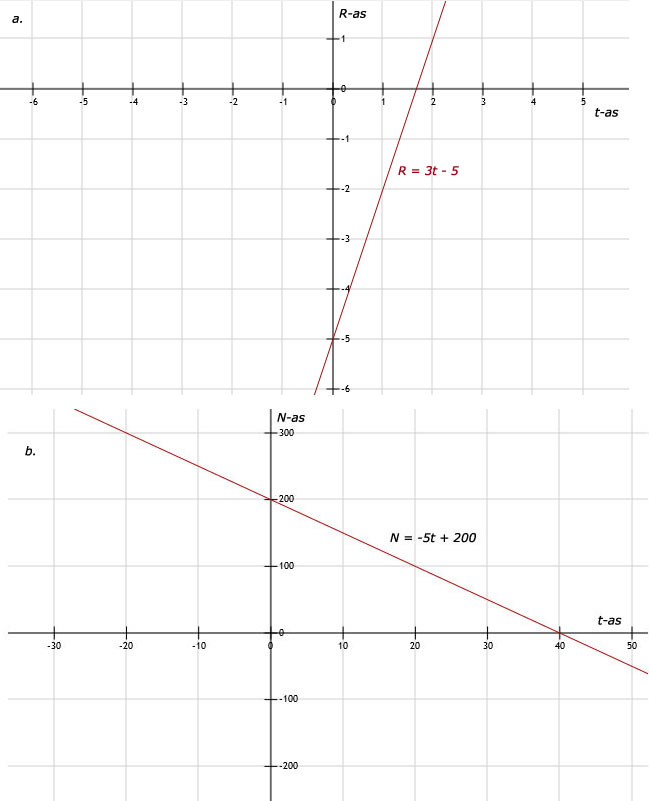
Zie afbeeldingOm een lijn te tekenen, heb je maar 2 punten nodig. Neem dan 2 makkelijke punten. Bijvoorbeeld de snijpunten met de x-as (0,b) en y-as.

33.
Tip:
Om te bepalen of een punt A(2,3) op een lijn l: ligt, vul x = 2 in en kijk of de y-waarde van de lijn l: gelijk is aan 3. Zoja, dan ligt het punt A op de lijn l:.
Gegeven de lijn l: y = 8x - 13.Om te bepalen of een punt A(2,3) op een lijn l: ligt, vul x = 2 in en kijk of de y-waarde van de lijn l: gelijk is aan 3. Zoja, dan ligt het punt A op de lijn l:.
a. Vul in x = 7. Dit levert y = 56 - 13 = 43. Dus het punt P(7,43) ligt op de lijn l:.
b. Vul in x = 10. Dit levert y = 80 - 13 = 67. Dus het punt P(10,93) ligt niet op de lijn. Maar punt (10,67) dus wel.
c. Vul in x = -4. Dit levert y = -45. Dus het punt A(-4,-45) ligt op de lijn.
d. Vul B(20,p) in l: levert: p = 8 x 20 - 13 = 147. Dus p = 147.
34.
a. a = 64
b. b = 1/7
c. c = 1
35.
a. Achtlo hoort bij N = 30t + 1800. Want 1800 is het snijpunt met de y-as bij t = 0.
b. Los op: 18t + 2100 = 30t + 1800, levert t = 25.
c. 18t + 2100 + 30t + 1800 = 5000 levert bij t = 1100/48 ≈ 22,91.
36.
a. Omdat er ieder jaar steeds een gelijke daling is van 3000 bedrijven.
b. Aantal bedrijven op 1 januari zou kunnen zijn: 92 + 3 + 3 -> 98 000
c. 3 000
d. N = -3t + 98
e. *
37.
a. Snijpunt met de y-as is (0,1). Dus b = 1.
b. De grafiek gaat 4 naar rechts en 3 omhoog. Ofwel 1 naar rechts en 3/4 omhoog.
c. Dus a = 3/4.
d. De formule van deze lijn wordt dan: y = 3/4x + 1

38.
Tip:
Lijnen die evenwijdig zijn, hebben dezelfde richtingscoëfficient. Dus dezelfde 'a'.
a. Lijnen die evenwijdig zijn, hebben dezelfde richtingscoëfficient. Dus dezelfde 'a'.
De formule van lijn l: is: y = x + 2
De formule van lijn m: is: y = -1½x + 1
De formule van lijn n: is: y = -1/3x + 4
b. De formule van lijn k: is: y = -1/3x - 3
39.
Tip:
a = rc = verticaal / horizontaal
De formule van lijn p: is: y = -2/5x + 3a = rc = verticaal / horizontaal
De formule van lijn q: is: y = ½x - 1½
De formule van lijn r: is: y = -2x
40.
a. Snijpunt met de B-as is (0,50) dus b = 50.
a = rc = verticaal / horizontaal = 50/20 = 2½
b. k: B = -6⅔t + 250
c. m: B = -5t + 150
41.
a. Formule van het aantal koopwoningen is N = 0,06t + 3,3.
b. Neem t = 19 levert N = 4,44.
c. Neem t = 14 levert N = 4,14.
42.
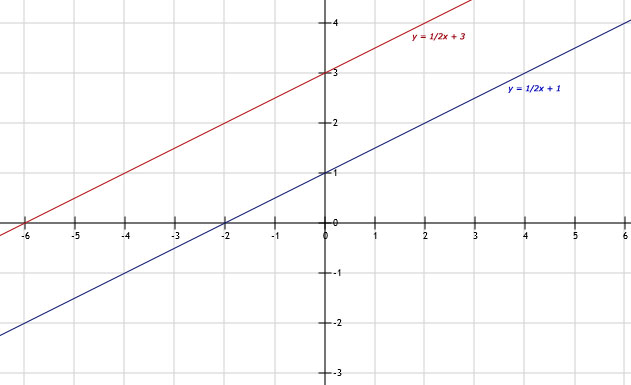
b. Zie afbeelding: 2 punten: (0,1) en (2,2)
c. Snijpunt y-as is (0,b) dus ze heeft voor 8 gekozen.
d. Grafiek door (8,0) dus invullen levert: y = 1/2 x 8 + b = 4 + b.
4 + b = 0 levert b = -4. Ze heeft dus voor -4 gekozen.
43.
44.
12 = 2 ⋅ 8 + b
b = -4
Dus: b = -4
45.
b = 0,5
46.
47.
48.
49.
b. m: y = -2/5x - 3/5
a. Snijpunt met de B-as is (0,50) dus b = 50.
a = rc = verticaal / horizontaal = 50/20 = 2½
b. k: B = -6⅔t + 250
c. m: B = -5t + 150
41.
a. Formule van het aantal koopwoningen is N = 0,06t + 3,3.
b. Neem t = 19 levert N = 4,44.
c. Neem t = 14 levert N = 4,14.
42.
Tip:
Om een rechte lijn te tekenen, heb je genoeg aan 2 punten. Vul x = 0 in en je hebt dan meteen al het snijpunt met de y-as. Als 1e punt x = 0 kiezen, is altijd de gemakkelijkste.
a. Zie afbeelding: 2 punten: (0,3) en (2,4)Om een rechte lijn te tekenen, heb je genoeg aan 2 punten. Vul x = 0 in en je hebt dan meteen al het snijpunt met de y-as. Als 1e punt x = 0 kiezen, is altijd de gemakkelijkste.
b. Zie afbeelding: 2 punten: (0,1) en (2,2)
c. Snijpunt y-as is (0,b) dus ze heeft voor 8 gekozen.
d. Grafiek door (8,0) dus invullen levert: y = 1/2 x 8 + b = 4 + b.
4 + b = 0 levert b = -4. Ze heeft dus voor -4 gekozen.

43.
Tip:
Lijnen die evenwijdig zijn, hebben dezelfde richtingscoëfficient. Dus dezelfde 'a'.
Hij heeft 8 gekozen.Lijnen die evenwijdig zijn, hebben dezelfde richtingscoëfficient. Dus dezelfde 'a'.
44.
Tip:
Vul het punt A(8,12) in en je krijgt b. Bij (8,12) is de x gelijk aan 8 en de y gelijk aan 12.
(x,y) <-> (8,12)
y = 2x + bVul het punt A(8,12) in en je krijgt b. Bij (8,12) is de x gelijk aan 8 en de y gelijk aan 12.
(x,y) <-> (8,12)
12 = 2 ⋅ 8 + b
b = -4
Dus: b = -4
45.
b = 0,5
46.
Tip:
Evenwijdig dus a = rck = rcl = 5, om b te bepalen vul P(1,6) in y = 5x + b.
a = 5 en b = 1, dus de formule van lijn k: is y = 5x + 1.Evenwijdig dus a = rck = rcl = 5, om b te bepalen vul P(1,6) in y = 5x + b.
47.
Tip:
Evenwijdig dus a = rcp = rcq = -2, om b te bepalen vul S(-5,-1) in y = -2x + b.
a = -2 en b = -11, dus de formule van lijn p: is y = -2x - 11.Evenwijdig dus a = rcp = rcq = -2, om b te bepalen vul S(-5,-1) in y = -2x + b.
48.
Tip:
Evenwijdig dus a = rcp = rcl = 5, om b te bepalen vul R(8,-16) in y = 5x + b. Dit levert b = -56.
De formule van lijn l: is y = 5x - 56Evenwijdig dus a = rcp = rcl = 5, om b te bepalen vul R(8,-16) in y = 5x + b. Dit levert b = -56.
49.
Tip:
rcl = verticaal / horizontaal = 2/4 = 1/2
rcm = verticaal / horizontaal = -2/5
a. l: y = ½x + 2½rcl = verticaal / horizontaal = 2/4 = 1/2
rcm = verticaal / horizontaal = -2/5
b. m: y = -2/5x - 3/5

Andere paragrafen:
1.1. Lineaire vergelijkingen (1 t/m 15)
1.2. Lineaire ongelijkheden (16 t/m 29)
1.3. Lineaire formules (30 t/m 49)
1.4. Lineaire functies (50 t/m 61)
1.5. Snijpunten van grafieken (62 t/m 73)
1.1. Lineaire vergelijkingen (1 t/m 15)
1.2. Lineaire ongelijkheden (16 t/m 29)
1.3. Lineaire formules (30 t/m 49)
1.4. Lineaire functies (50 t/m 61)
1.5. Snijpunten van grafieken (62 t/m 73)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


