TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 1.4 Lineaire functies VWO 3
Boek: Getal & Ruimte - Lineaire problemen VWO 3 (deel 1) opgaven 50 t/m 61, 2011De basisformulering van een formule is van de vorm: y = ax + b. We kunnen ook de haakjesnotatie gebruiken: f(x) = ax + b.
Dus bij de formule y = 4x - 5 hoort de functie f(x) = 4x - 5. Het is een andere manier van noteren, maar het gaat over hetzelfde.
Een functie moet je zien als een soort machientje. Je stopt er iets in, en er komt iets uit. Wat je er in stopt, is 'x' en wat er uitkomt, is 'y'.
Zo levert f(3) als uitkomst 7. We noemen 3 dan het origineel en 7 het beeld (of functiewaarde).
Dus bij de formule y = 4x - 5 hoort de functie f(x) = 4x - 5. Het is een andere manier van noteren, maar het gaat over hetzelfde.
Een functie moet je zien als een soort machientje. Je stopt er iets in, en er komt iets uit. Wat je er in stopt, is 'x' en wat er uitkomt, is 'y'.
Zo levert f(3) als uitkomst 7. We noemen 3 dan het origineel en 7 het beeld (of functiewaarde).
50.
a. 2 x 5 + 8 = 10 + 8 = 18 dus een ritje van 5 km kost € 18,=.
2 x 12 + 8 = 24 + 8 = 32 dus een ritje van 12 km kost € 32,=.
b. De formule die hoort bij een taxirit: y = 2x + 8
51.
a. Het beeld van 5: 7 x 5 - 4 = 35 - 4 = 31
b. Het beeld van -4: 7 x -4 - 4 = -28 - 4 = -32
c. y = 7x - 4
52.
a. Het beeld van 18: 1/2 x 18 + 6 = 9 + 6 = 15
b.
c. y = ½x + 6
53.
b. Bij x = -3 hoort y = -3 ⋅ -3 + 18 = 27. Dus bij origineel x = -3 hoort beeld y = 27.
54.
f(3) = -4 ⋅ 3 + 9 = -12 + 9 = -3
f(8) = -4 ⋅ 8 + 9 = -32 + 9 = -23
b. g(-8) = -(-8) = 8
g(7) = -(7) = -7
g(0) = -(0) = 0
c. f(5) + g(3) = -11 - 3 = -14
d. De formule die hoort bij de functie van f: y = -4x + 9
De formule die hoort bij de functie van g: y = -x
55.
g(8) = -3 ⋅ (8 - 7) = -3 ⋅ 1 = -3
b. f(-2) = 7 ⋅ -2 - 8 = -14 - 8 = -22
g(-2) = -3 ⋅ (-2 - 7) = -3 ⋅ -9 = 27
c. f(0) = 7 ⋅ 0 - 8 = 0 - 8 = -8
d. f(7) + g(7) = 41 + 0 = 41
e. De formule die hoort bij de functie g is y = -3(x - 7) of y = -3x + 21
56.
b. Zie afbeelding
c. f(-3) levert y = 13, dus (-3,13) ligt op de grafiek van f.
d. f(80) levert y = -153, dus (80,-167) ligt niet op de grafiek van f.
e. f(x) = 21, dus -2x + 7 = 21 hieruit volgt x = -7.
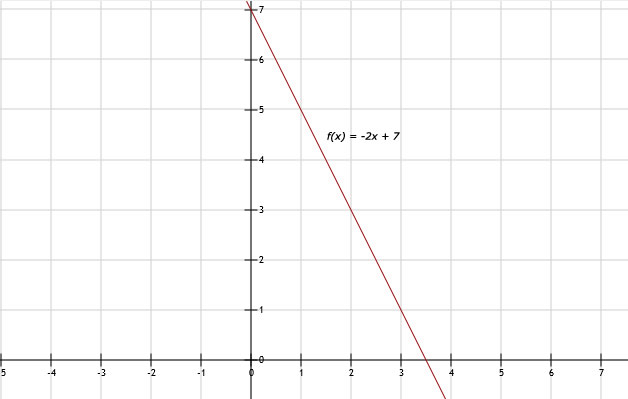
57.
Zie afbeelding
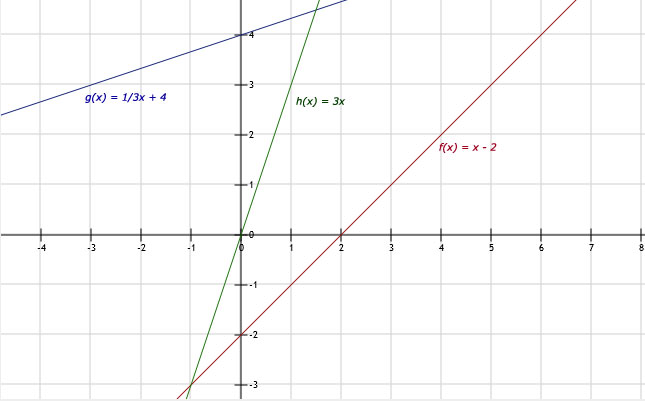
58.
a. Zie afbeelding
b. Het punt A(12,21) ligt op de grafiek van f, want f(12) = 21.
c. Het punt B(-18,-28) ligt niet op de grafiek van g, want g(-18) = -26.
d. g(x) = -8 levert XP = -6
e. f(x) = 0 levert XQ = 1½
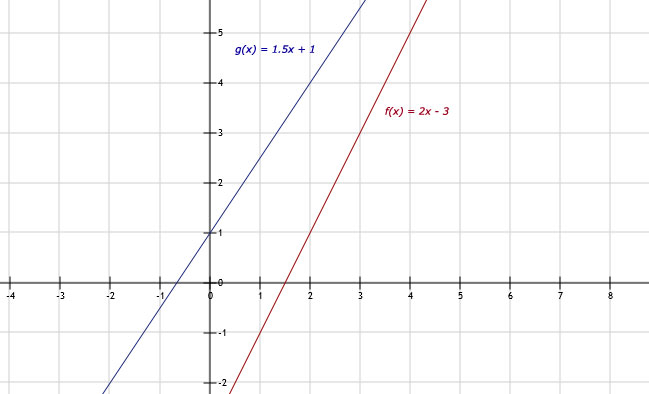
59.
a. Door (-8,80) levert:
80 = -8a + 8
-8a = 72
a = -9
b. Evenwijdig aan y = -5x + 6 levert dezelfde rc, dus a = -5.
c. Door (-5,a) levert:
a = -5a + 8
6a = 8
a = 8/6 = 4/3 = 1⅓
d. Door (a,24) levert:
24 = a x a + 8
24 = a2 + 8
a2 = 16
a = 4 v a = -4
a. 2 x 5 + 8 = 10 + 8 = 18 dus een ritje van 5 km kost € 18,=.
2 x 12 + 8 = 24 + 8 = 32 dus een ritje van 12 km kost € 32,=.
b. De formule die hoort bij een taxirit: y = 2x + 8
51.
a. Het beeld van 5: 7 x 5 - 4 = 35 - 4 = 31
b. Het beeld van -4: 7 x -4 - 4 = -28 - 4 = -32
c. y = 7x - 4
52.
a. Het beeld van 18: 1/2 x 18 + 6 = 9 + 6 = 15
b.
| origineel | -3 | 0 | 5 | 8 |
| beeld | 4,5 | 6 | 8,5 | 10 |
c. y = ½x + 6
53.
Tip:
f(4) = 6, dat wil zeggen dat bij de functie f is het origineel gelijk aan 4 en het beeld is 6.
a. Bij x = 4 hoort y = -3 ⋅ 4 + 18 = 6. Dus bij origineel x = 4 hoort beeld y = 6.f(4) = 6, dat wil zeggen dat bij de functie f is het origineel gelijk aan 4 en het beeld is 6.
b. Bij x = -3 hoort y = -3 ⋅ -3 + 18 = 27. Dus bij origineel x = -3 hoort beeld y = 27.
54.
Tip:
f(-5) = 29 betekent dat het punt (-5, 29) op de grafiek ligt.
a. f(-5) = -4 ⋅ -5 + 9 = 20 + 9 = 29f(-5) = 29 betekent dat het punt (-5, 29) op de grafiek ligt.
f(3) = -4 ⋅ 3 + 9 = -12 + 9 = -3
f(8) = -4 ⋅ 8 + 9 = -32 + 9 = -23
b. g(-8) = -(-8) = 8
g(7) = -(7) = -7
g(0) = -(0) = 0
c. f(5) + g(3) = -11 - 3 = -14
d. De formule die hoort bij de functie van f: y = -4x + 9
De formule die hoort bij de functie van g: y = -x
55.
Tip:
Bij f(0) is dus x = 0 en is dus ook het snijpunt met de y-as.
a. f(8) = 7 ⋅ 8 - 8 = 56 - 8 = 48Bij f(0) is dus x = 0 en is dus ook het snijpunt met de y-as.
g(8) = -3 ⋅ (8 - 7) = -3 ⋅ 1 = -3
b. f(-2) = 7 ⋅ -2 - 8 = -14 - 8 = -22
g(-2) = -3 ⋅ (-2 - 7) = -3 ⋅ -9 = 27
c. f(0) = 7 ⋅ 0 - 8 = 0 - 8 = -8
d. f(7) + g(7) = 41 + 0 = 41
e. De formule die hoort bij de functie g is y = -3(x - 7) of y = -3x + 21
56.
Tip:
Bij het punt A(2,3) geldt het volgende: XA = 2 en YA = 3.
Dus XA is de x-coördinaat van het punt A en YA is de y-coördinaat van het punt A.
a. f(3) = 1 en f(-2) = 11Bij het punt A(2,3) geldt het volgende: XA = 2 en YA = 3.
Dus XA is de x-coördinaat van het punt A en YA is de y-coördinaat van het punt A.
b. Zie afbeelding
c. f(-3) levert y = 13, dus (-3,13) ligt op de grafiek van f.
d. f(80) levert y = -153, dus (80,-167) ligt niet op de grafiek van f.
e. f(x) = 21, dus -2x + 7 = 21 hieruit volgt x = -7.

57.
Zie afbeelding

58.
a. Zie afbeelding
b. Het punt A(12,21) ligt op de grafiek van f, want f(12) = 21.
c. Het punt B(-18,-28) ligt niet op de grafiek van g, want g(-18) = -26.
d. g(x) = -8 levert XP = -6
e. f(x) = 0 levert XQ = 1½

59.
Tip:
Bij vraag d.
Als (a,24) op de lijn y = ax + 8 ligt dan vul je in deze lijn voor de x de waarde a in en voor de y de waarde 24. Dus je krijgt dan:
y = ax + 8 -> 24 = a ⋅ a + 8
Dit levert: 24 = a2 + 8 -> a = 4 of a = -4
Dus het punt (4,24) ligt op de lijn y = 4x + 8 en het punt (-4,24) ligt op de lijn y = -4x + 8.
Begin met y = ax + 8Bij vraag d.
Als (a,24) op de lijn y = ax + 8 ligt dan vul je in deze lijn voor de x de waarde a in en voor de y de waarde 24. Dus je krijgt dan:
y = ax + 8 -> 24 = a ⋅ a + 8
Dit levert: 24 = a2 + 8 -> a = 4 of a = -4
Dus het punt (4,24) ligt op de lijn y = 4x + 8 en het punt (-4,24) ligt op de lijn y = -4x + 8.
a. Door (-8,80) levert:
80 = -8a + 8
-8a = 72
a = -9
b. Evenwijdig aan y = -5x + 6 levert dezelfde rc, dus a = -5.
c. Door (-5,a) levert:
a = -5a + 8
6a = 8
a = 8/6 = 4/3 = 1⅓
d. Door (a,24) levert:
24 = a x a + 8
24 = a2 + 8
a2 = 16
a = 4 v a = -4
60.
Begin met y = 3x + b
a. Door (-5,20) levert:
20 = -15 + b
b = 35
b. Door (8,0) levert:
0 = 24 + b
b = -24
c. Door (b,12) levert:
12 = 3b + b
12 = 4b
b = 3
61.
Begin met y = ⅓ax + 12
a. Door (-6,20) levert:
20 = -2a + 12
-2a = 8
a = -4
b. Evenwijdig dus rc moet 9 zijn.
Dus rck = rcf
Dus 1/3a = 9
a = 27
c. Door (15,a) levert:
a = 1/3⋅a⋅15 + 12
a = 5a + 12
-4a = 12
a = -3
Begin met y = 3x + b
a. Door (-5,20) levert:
20 = -15 + b
b = 35
b. Door (8,0) levert:
0 = 24 + b
b = -24
c. Door (b,12) levert:
12 = 3b + b
12 = 4b
b = 3
61.
Begin met y = ⅓ax + 12
a. Door (-6,20) levert:
20 = -2a + 12
-2a = 8
a = -4
b. Evenwijdig dus rc moet 9 zijn.
Dus rck = rcf
Dus 1/3a = 9
a = 27
c. Door (15,a) levert:
a = 1/3⋅a⋅15 + 12
a = 5a + 12
-4a = 12
a = -3
Andere paragrafen:
1.1. Lineaire vergelijkingen (1 t/m 15)
1.2. Lineaire ongelijkheden (16 t/m 29)
1.3. Lineaire formules (30 t/m 49)
1.4. Lineaire functies (50 t/m 61)
1.5. Snijpunten van grafieken (62 t/m 73)
1.1. Lineaire vergelijkingen (1 t/m 15)
1.2. Lineaire ongelijkheden (16 t/m 29)
1.3. Lineaire formules (30 t/m 49)
1.4. Lineaire functies (50 t/m 61)
1.5. Snijpunten van grafieken (62 t/m 73)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


