TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 6.2 Rechthoekige driehoek VMBO 2 KGT
Boek: Getal & Ruimte - Stelling van Pythagoras VMBO 2 (deel 2) opgaven 19 t/m 29, 2009Een rechthoekige driehoek is een driehoek waarvan 1 hoek een rechte hoek is, oftewel gelijk is aan 90º (graden).
De langste zijde ligt tegenover de rechte hoek. De andere 2 zijden zitten vast aan de rechte hoek. Daarom noemen we deze rechthoekszijden.
19.
b. Driehoek e is gelijkzijdig.
c. Rechthoekige driehoeken zijn b, c, d, i en j.
d. Driehoeken b en i zijn zowel gelijkbenig als rechthoekig.
20.
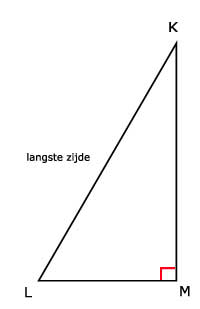
b. BC is de langste zijde, deze is 5 cm

21.
a. Zie afbeelding
b. PQ is de langste zijde, deze is 5 cm

22.
b. De langste zijde is de zijde met de andere 2 letters dan die van de rechte hoek.
23.
*
24.
a.
KLM: LM
DEF: DE
ABC: AB
PQR: QR
RST: RT
b.
KLM: KM en KL
DEF: EF en DF
ABC: AC en BC
PQR: PQ en PR
RST: RS en ST
25.
26.
a. ADHE is een rechthoek
b. en c. Zie afbeelding
d. Van driehoek ADH en driehoek AEH

27.
b. AC
c. EF en GF
d. ∠H is recht
28.
a. en b. Zie afbeelding
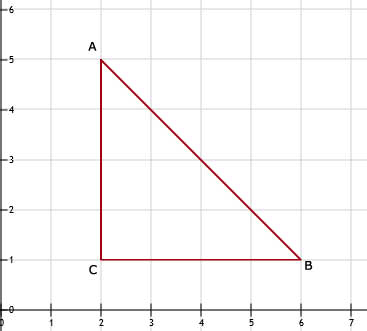
c. AB is de langste zijde
d. De 2 korte zijden zijn 4 cm
Tip:
Een gelijkzijdige driehoek is een bijzondere gelijkbenige driehoek.
a. Gelijkbenige driehoeken zijn: a, b en iEen gelijkzijdige driehoek is een bijzondere gelijkbenige driehoek.
b. Driehoek e is gelijkzijdig.
c. Rechthoekige driehoeken zijn b, c, d, i en j.
d. Driehoeken b en i zijn zowel gelijkbenig als rechthoekig.
20.
Tip:
Een rechte hoek (∠A) geven we aan met een (rode) winkelhaak.
a. Zie afbeeldingEen rechte hoek (∠A) geven we aan met een (rode) winkelhaak.
b. BC is de langste zijde, deze is 5 cm

21.
a. Zie afbeelding
b. PQ is de langste zijde, deze is 5 cm

22.
Tip:
Gegeven driehoek XYZ. Als ∠X de rechte hoek is, dan vormen de 2 overgebleven letters de langste zijde. Dus YZ is de langste / schuine zijde.
a. Zie afbeelding. Ja, het klopt wat hij zegt.Gegeven driehoek XYZ. Als ∠X de rechte hoek is, dan vormen de 2 overgebleven letters de langste zijde. Dus YZ is de langste / schuine zijde.
b. De langste zijde is de zijde met de andere 2 letters dan die van de rechte hoek.

23.
*
24.
a.
KLM: LM
DEF: DE
ABC: AB
PQR: QR
RST: RT
b.
KLM: KM en KL
DEF: EF en DF
ABC: AC en BC
PQR: PQ en PR
RST: RS en ST
25.
| driehoek | langste zijde | 2 korte zijden |
| ABC | AC | AB en BC |
| ABD | AB | AD en BD |
| BDE | BD | BE en DE |
| BDC | BC | BD en CD |
| DEC | DC | DE en CE |
26.
a. ADHE is een rechthoek
b. en c. Zie afbeelding
d. Van driehoek ADH en driehoek AEH

27.
Tip:
In een getekende kubus zijn er vele rechte hoeken die op het eerst gezicht niet recht lijken.
a. ∠B is rechtIn een getekende kubus zijn er vele rechte hoeken die op het eerst gezicht niet recht lijken.
b. AC
c. EF en GF
d. ∠H is recht
28.
a. en b. Zie afbeelding
c. AB is de langste zijde
d. De 2 korte zijden zijn 4 cm

29.
a. Zie afbeelding
b. R kan liggen op (3,3) en (-1,-2)
c. *
d. De 2 korte zijden zijn 4 en 5 cm.
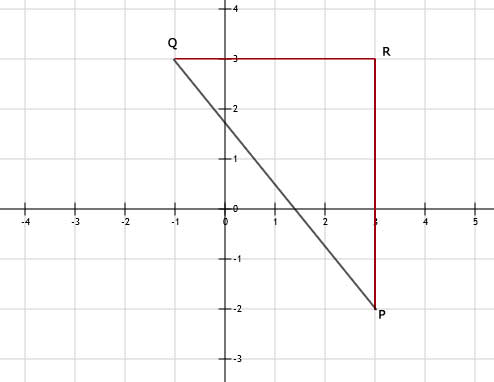
a. Zie afbeelding
b. R kan liggen op (3,3) en (-1,-2)
c. *
d. De 2 korte zijden zijn 4 en 5 cm.

Andere paragrafen:
6.1. Kwadraten en wortels (1 t/m 18)
6.2. Rechthoekige driehoek (19 t/m 29)
6.3. De stelling van Pythagoras (30 t/m 40)
6.4. Toepassingen van Pythagoras (41 t/m 52)
6.5. Gemengde opgaven (53 t/m 61)
6.1. Kwadraten en wortels (1 t/m 18)
6.2. Rechthoekige driehoek (19 t/m 29)
6.3. De stelling van Pythagoras (30 t/m 40)
6.4. Toepassingen van Pythagoras (41 t/m 52)
6.5. Gemengde opgaven (53 t/m 61)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


