TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 6.4 Toepassingen van Pythagoras VMBO 2 KGT
Boek: Getal & Ruimte - Stelling van Pythagoras VMBO 2 (deel 2) opgaven 41 t/m 52, 2009Je kunt onderzoeken of een driehoek rechthoekig is. Als de Stelling van Pythagoras in die driehoek geldt, dan is de hoek een rechte hoek.
Trek een hulplijn in een figuur om een rechthoekige driehoek te krijgen. Pas dan de Stelling van Pythagoras toe.
Ook om de afstand tussen roosterpunten te berekenen, maken we gebruik van de Stelling van Pythagoras.
Trek een hulplijn in een figuur om een rechthoekige driehoek te krijgen. Pas dan de Stelling van Pythagoras toe.
Ook om de afstand tussen roosterpunten te berekenen, maken we gebruik van de Stelling van Pythagoras.
41.
b. Ja het klopt, want 64 + 36 = 100
42.
Driehoek ABC is rechthoekig in hoek C
Driehoek DEF is niet rechthoekig
Driehoek KLM is rechthoekig in hoek L
43.
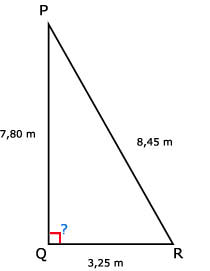
44.
c. BC = √1,8 ≈ 1,342 km ≈ 1342 meter
d. Dat is 458 meter korter
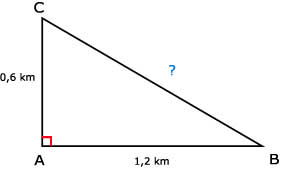
45.
BD ≈ 2,75
Hoogte lokaal is dus 3,5 m
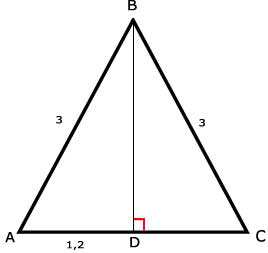
46.
CD ≈ 3,20 m
47.
BC = 10 m
Omtrek is 42 meter
48.
BC ≈ 2,84 m
Hoogte kas is dus: 3,2m + 2,84m = 6,04 meter.
En dat is 604 cm.
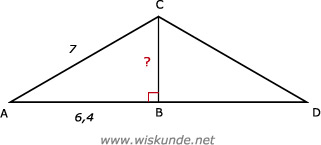
49.
b. DC = √45 ≈ 6,71 cm
50.
EF = √40 ≈ 6,32 cm
Tip:
Omdat geldt: 64 + 36 = 100 weten we zeker dat de hoek recht is.
a.
Omdat geldt: 64 + 36 = 100 weten we zeker dat de hoek recht is.
| korte zijde | AC = 8 | | | 64 |
| korte zijde | BC = 6 | | | 36 |
| langste zijde | AB = 10 | | | 100 |
b. Ja het klopt, want 64 + 36 = 100
42.
Driehoek ABC is rechthoekig in hoek C
Driehoek DEF is niet rechthoekig
Driehoek KLM is rechthoekig in hoek L
43.
Tip:
Geldt: 3,252 + 7,802 = 8,452 ?
Ja, dat klopt, dus de hoeken zijn recht. Dus de paal staat recht.Geldt: 3,252 + 7,802 = 8,452 ?

44.
Tip:
1 km = 1000 m
a. en b. Zie afbeelding1 km = 1000 m
c. BC = √1,8 ≈ 1,342 km ≈ 1342 meter
d. Dat is 458 meter korter

45.
Tip:
Hoogte ladder + 75 cm is hoogte lokaal.
BD2 = 7,56Hoogte ladder + 75 cm is hoogte lokaal.
BD ≈ 2,75
Hoogte lokaal is dus 3,5 m

46.
Tip:
Je krijgt een driehoek met korte zijden: 2,5 m en 2 m
CD2 = 10,25Je krijgt een driehoek met korte zijden: 2,5 m en 2 m
CD ≈ 3,20 m
47.
Tip:
Omtrek is de som van AB + BC + CD + AD
BC2 = 100Omtrek is de som van AB + BC + CD + AD
BC = 10 m
Omtrek is 42 meter
48.
Tip:
Maak een rechthoekige driehoek ABC met zijden: AB = 6,4 en AC = 7 (langste) en hoogte BC. Deze hoogte is dan 2,84 m. Tel daar 3,2 bij op en reken dan om naar cm.
BC = √8,04Maak een rechthoekige driehoek ABC met zijden: AB = 6,4 en AC = 7 (langste) en hoogte BC. Deze hoogte is dan 2,84 m. Tel daar 3,2 bij op en reken dan om naar cm.
BC ≈ 2,84 m
Hoogte kas is dus: 3,2m + 2,84m = 6,04 meter.
En dat is 604 cm.

49.
Tip:
De ene korte zijde is het verschil in de x-waarden en de andere korte zijde is het verschil in de y-waarden.
a. AB = √25 = 5 cmDe ene korte zijde is het verschil in de x-waarden en de andere korte zijde is het verschil in de y-waarden.
b. DC = √45 ≈ 6,71 cm
50.
EF = √40 ≈ 6,32 cm
51.
a. *
b. Omtrek driehoek ABC ≈ 15,3 cm.
52.
a. *
b. Omtrek driehoek ABC ≈ 15,3 cm.
52.
Tip:
Bereken 4x de langste zijde van 4 rechthoekige driehoeken.
Omtrek van parallellogram = 18,4 cmBereken 4x de langste zijde van 4 rechthoekige driehoeken.
Andere paragrafen:
6.1. Kwadraten en wortels (1 t/m 18)
6.2. Rechthoekige driehoek (19 t/m 29)
6.3. De stelling van Pythagoras (30 t/m 40)
6.4. Toepassingen van Pythagoras (41 t/m 52)
6.5. Gemengde opgaven (53 t/m 61)
6.1. Kwadraten en wortels (1 t/m 18)
6.2. Rechthoekige driehoek (19 t/m 29)
6.3. De stelling van Pythagoras (30 t/m 40)
6.4. Toepassingen van Pythagoras (41 t/m 52)
6.5. Gemengde opgaven (53 t/m 61)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


