TIP: Wil je ook toegang tot meer dan 16.500 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 2.1 Kruisproducten HAVO 3
Boek: Getal & Ruimte - Gelijkvormigheid HAVO 3 (deel 1) opgaven 1 t/m 16, 2010Wat zijn kruisproducten?
In een verhoudingstabel kunnen we kruisproducten maken.
Daarbij vermenigvuldigen we de waarde linksboven met de waarde rechtsonder.
En we vermenigvuldigen de waarde rechtsboven met de waarde linksonder. De uitkomsten zijn gelijk aan elkaar.
Bijvoorbeeld: 10 x 60 = 20 x 30. Op deze manier kunnen we ontbrekende waarde berekenen in een verhoudingstabel.
Later gaan we kruisproducten gebruiken in gelijkvormige driehoeken om de lengte van zijden te berekenen.
In een verhoudingstabel kunnen we kruisproducten maken.
Daarbij vermenigvuldigen we de waarde linksboven met de waarde rechtsonder.
En we vermenigvuldigen de waarde rechtsboven met de waarde linksonder. De uitkomsten zijn gelijk aan elkaar.
Bijvoorbeeld: 10 x 60 = 20 x 30. Op deze manier kunnen we ontbrekende waarde berekenen in een verhoudingstabel.
Later gaan we kruisproducten gebruiken in gelijkvormige driehoeken om de lengte van zijden te berekenen.
1.
b.
2.
10 x 21 = 14 x 15 (210)
Je ziet dat de uitkomsten gelijk zijn.
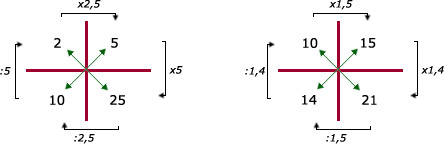
3.
2 ⋅ x = 28
x = 14
b.
2,3 ⋅ 12 = 4 ⋅ x
27,6 = 4x
4x = 27,6
x = 6,9
c.
18 ⋅ 20 = 16 ⋅ x
360 = 16x
16x = 360
x = 22,5
d.
x ⋅ 8 = 6,8 ⋅ 5,2
8x = 35,36
x = 4,42
4.
a.
9 ⋅ x = 5 ⋅ 30
9x = 150
x = 16,7
b.
15 ⋅ x = 8 ⋅ 95
15x = 760
x = 50,7
c.
15,3 ⋅ 7,6 = x ⋅ 27,8
27,8x = 116,28
x = 4,2
d.
x ⋅ 0,7 = 2,7 ⋅ 3,1
0,7x = 8,37
x = 12,0
5.
b. 3(x + 3) = 5(x - 1)
3x + 9 = 5x - 5
-2x = -14
x = 7
6.
a.
2(x - 5) = 7(x + 1)
2x - 10 = 7x + 7
-5x = 17
x = -17/5
x = -3,4
b.
3(2x + 1) = 4(x - 1)
6x + 3 = 4x - 4
2x = -7
x = -3,5
c.
7,9x = 2,3(3x + 2)
7,9x = 6,9x + 4,6
7,9x - 6,9x = 4,6
x = 4,6
7.
50a = 16 x 43
a = (16 x 43) / 50
a = 13,76
16b = 50 x 50
b = (50 x 50) / 16
b = 156,25
b.
32c = 17 x 80
c = (17 x 80) / 32
c = 42,5
80d = 32 x 15
d = (32 x 15) / 80
d = 6
8.
a.
11p = 5 x 18
p = (5 x 18) / 11
p ≈ 8,2
18q = 11 x 10
q = (11 x 10) / 18
q ≈ 6,1
b.
2,1r = 5 x 1,6
r = (5 x 1,6) / 2,1
r ≈ 3,8
2,1s = 1,6 x 1,5
s = (1,6 x 1,5) / 2,1
s ≈ 1,1
9.
x = (18 x 17) / 23
x ≈ 13,30
23y = 18 x 53
y = (18 x 53) / 23
y ≈ 41,48
18z = 23 x 73
z = (23 x 73) / 18
z ≈ 93,28
10.
23(2x + 1) = 18 x 17
46x + 23 = 306
46x = 283
x ≈ 6,15
23(2y - 3) = 18(y + 1)
46y - 69 = 18y + 18
28y = 87
y = 87/28
y ≈ 3,11
b.
15x = 7(x + 3)
15x = 7x + 21
8x = 21
x = 21/8
x ≈ 2,63
7y = 15(y - 5)
7y = 15y - 75
-8y = -75
y = -75/-8
y ≈ 9,38
Tip:
Bij a. van bovenste rij naar de onderste rij steeds :18
Bij b. van bovenste rij naar de onderste rij steeds :22
a. Bij a. van bovenste rij naar de onderste rij steeds :18
Bij b. van bovenste rij naar de onderste rij steeds :22
| diameter velg in cm | 36 | 27 | 14,4 | 40,5 |
| breedte velg in cm | 2 | 1,5 | 0,8 | 2,25 |
b.
| diameter velg in cm | 99 | 61,6 | 38,5 |
| breedte velg in cm | 4,5 | 2,8 | 1,75 |
2.
Tip:
Bij een verhoudingstabel zijn de diverse kruisproducten gelijk.
Als er geen sprake is van een verhoudingstabel dan zijn de uitkomsten dus niet gelijk.
2 x 25 = 10 x 5 (50)Bij een verhoudingstabel zijn de diverse kruisproducten gelijk.
Als er geen sprake is van een verhoudingstabel dan zijn de uitkomsten dus niet gelijk.
10 x 21 = 14 x 15 (210)
Je ziet dat de uitkomsten gelijk zijn.
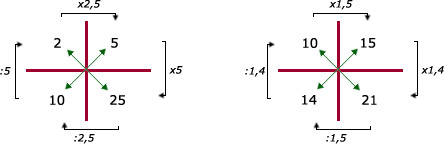
3.
Tip:
(puntje ertussen)
x⋅5 is hetzelfde als 5⋅x is hetzelfde als 5x
a. (puntje ertussen)
x⋅5 is hetzelfde als 5⋅x is hetzelfde als 5x
2 ⋅ x = 28
x = 14
b.
2,3 ⋅ 12 = 4 ⋅ x
27,6 = 4x
4x = 27,6
x = 6,9
c.
18 ⋅ 20 = 16 ⋅ x
360 = 16x
16x = 360
x = 22,5
d.
x ⋅ 8 = 6,8 ⋅ 5,2
8x = 35,36
x = 4,42
4.
a.
9 ⋅ x = 5 ⋅ 30
9x = 150
x = 16,7
b.
15 ⋅ x = 8 ⋅ 95
15x = 760
x = 50,7
c.
15,3 ⋅ 7,6 = x ⋅ 27,8
27,8x = 116,28
x = 4,2
d.
x ⋅ 0,7 = 2,7 ⋅ 3,1
0,7x = 8,37
x = 12,0
5.
Tip:
Vul de uitkomst x = 7 maar in in de tabel. Je krijgt dan de verhoudingstabel 3 / 5 met 6 / 10 en dat klopt.
En kruisproduct 5 x 6 = 3 x 10 klopt ook.
a. kruisproduct: 3(x + 3) = 5(x - 1)Vul de uitkomst x = 7 maar in in de tabel. Je krijgt dan de verhoudingstabel 3 / 5 met 6 / 10 en dat klopt.
En kruisproduct 5 x 6 = 3 x 10 klopt ook.
b. 3(x + 3) = 5(x - 1)
3x + 9 = 5x - 5
-2x = -14
x = 7
6.
a.
2(x - 5) = 7(x + 1)
2x - 10 = 7x + 7
-5x = 17
x = -17/5
x = -3,4
b.
3(2x + 1) = 4(x - 1)
6x + 3 = 4x - 4
2x = -7
x = -3,5
c.
7,9x = 2,3(3x + 2)
7,9x = 6,9x + 4,6
7,9x - 6,9x = 4,6
x = 4,6
7.
Tip:
Om 'b' te berekenen heb je 2 mogelijkheden:
1. Gebruik het kruisproduct van 16 x b = 50 x 50 (aangeraden)
2. Bereken eerst 'a' en gebruik dat antwoord in het kruisproduct om 'b' te berekenen
a.Om 'b' te berekenen heb je 2 mogelijkheden:
1. Gebruik het kruisproduct van 16 x b = 50 x 50 (aangeraden)
2. Bereken eerst 'a' en gebruik dat antwoord in het kruisproduct om 'b' te berekenen
50a = 16 x 43
a = (16 x 43) / 50
a = 13,76
16b = 50 x 50
b = (50 x 50) / 16
b = 156,25
b.
32c = 17 x 80
c = (17 x 80) / 32
c = 42,5
80d = 32 x 15
d = (32 x 15) / 80
d = 6
8.
a.
11p = 5 x 18
p = (5 x 18) / 11
p ≈ 8,2
18q = 11 x 10
q = (11 x 10) / 18
q ≈ 6,1
b.
2,1r = 5 x 1,6
r = (5 x 1,6) / 2,1
r ≈ 3,8
2,1s = 1,6 x 1,5
s = (1,6 x 1,5) / 2,1
s ≈ 1,1
9.
Tip:
Maak bij elke kruisproduct steeds gebruik van de verhouding 18 / 23
23x = 18 x 17Maak bij elke kruisproduct steeds gebruik van de verhouding 18 / 23
x = (18 x 17) / 23
x ≈ 13,30
23y = 18 x 53
y = (18 x 53) / 23
y ≈ 41,48
18z = 23 x 73
z = (23 x 73) / 18
z ≈ 93,28
10.
Tip:
Ook hier maak bij elk kruisproduct steeds gebruik van de verhouding 18 / 23 (opgave a.) en 15 / 7 (opgave b.).
a.Ook hier maak bij elk kruisproduct steeds gebruik van de verhouding 18 / 23 (opgave a.) en 15 / 7 (opgave b.).
23(2x + 1) = 18 x 17
46x + 23 = 306
46x = 283
x ≈ 6,15
23(2y - 3) = 18(y + 1)
46y - 69 = 18y + 18
28y = 87
y = 87/28
y ≈ 3,11
b.
15x = 7(x + 3)
15x = 7x + 21
8x = 21
x = 21/8
x ≈ 2,63
7y = 15(y - 5)
7y = 15y - 75
-8y = -75
y = -75/-8
y ≈ 9,38
11.
*
12.
6 kubussen -> 9 cm (dus x1,5)
b. 24/1,5 = 24:1,5 levert dus 16 kubussen
c.
13.
=>
B'C' = (3 x 5) / 2 = 7,5
C'D' = (3 x 6) / 2 = 9
14.
a = (22 x 30) / 20 = 33
b = (18 x 22) / 20 = 19,8
c = (22 x 15) / 20 = 16,5
15.
a. y = (22 x 40) / 32 = 27,5
Hoogte van de toren = 27,5 + 20 + 40 = 87,5 meter
b. x = (20 x 32) / 40 = 16
Hoogte van de schaduw = 22 + 16 + 32 = 70 meter
16.
PS = PQ + QR + RS
PS = (x + 2) + (x + 1) + x
PS = 3x + 3
=>
17,50(x + 1) = 18,75x
17,50x + 17,50 = 18,75x
-1,25x = -17,50
x = 14
Als RS = x = 14 dan:
QR = x + 1 = 14 + 1 = 15
PQ = x + 2 = 14 + 2 = 16
PS = 3x + 3 = 3*14 + 3 = 55
b.
P'Q' = 18,75(x + 2) / (x + 1)
Invullen x = 14 levert:
P'Q' = 20
*
12.
Tip:
Van aantal kubussen naar lengte schaduw => x1,5
Van lengte schaduw naar aantal kubussen => :1,5
a. 4 kubussen -> 6 cm (dus x1,5)Van aantal kubussen naar lengte schaduw => x1,5
Van lengte schaduw naar aantal kubussen => :1,5
6 kubussen -> 9 cm (dus x1,5)
b. 24/1,5 = 24:1,5 levert dus 16 kubussen
c.
| aantal kubussen | 4 | 6 | 16 | 20 | 40 |
| lengte schaduw | 6 | 9 | 24 | 30 | 60 |
13.
| AB | BC | CD |
| A'B' | B'C' | C'D' |
| 2 | 5 | 6 |
| 3 | B'C' | C'D' |
B'C' = (3 x 5) / 2 = 7,5
C'D' = (3 x 6) / 2 = 9
14.
Tip:
Neem 20 / 22 als basis voor al je kruisproducten. Maar dat hoeft niet. Je kunt om 'b' te berekenen ook 30 / 33 (als je 'a' hebt) gebruiken.
Neem 20 / 22 als basis voor al je kruisproducten. Maar dat hoeft niet. Je kunt om 'b' te berekenen ook 30 / 33 (als je 'a' hebt) gebruiken.
| 20 | 30 | 18 | 15 |
| 22 | a | b | c |
a = (22 x 30) / 20 = 33
b = (18 x 22) / 20 = 19,8
c = (22 x 15) / 20 = 16,5
15.
Tip:
Maak een verhoudingstabel met in de eerste rij de afmetingen van de torenstukken en in de tweede rij de afmetingen van de schaduwstukken.
Tevens: hoogte toren = y + 20 + 40.
Maak een verhoudingstabel met in de eerste rij de afmetingen van de torenstukken en in de tweede rij de afmetingen van de schaduwstukken.
Tevens: hoogte toren = y + 20 + 40.
| y | 20 | 40 |
| 22 | x | 32 |
a. y = (22 x 40) / 32 = 27,5
Hoogte van de toren = 27,5 + 20 + 40 = 87,5 meter
b. x = (20 x 32) / 40 = 16
Hoogte van de schaduw = 22 + 16 + 32 = 70 meter
16.
Tip:
Als RS = x dan is:
QR = x + 1
PQ = x + 2
a.Als RS = x dan is:
QR = x + 1
PQ = x + 2
PS = PQ + QR + RS
PS = (x + 2) + (x + 1) + x
PS = 3x + 3
| PQ | QR | RS |
| P'Q' | Q'R' | R'S' |
| x + 2 | x + 1 | x |
| P'Q' | 18,75 | 17,50 |
17,50(x + 1) = 18,75x
17,50x + 17,50 = 18,75x
-1,25x = -17,50
x = 14
Als RS = x = 14 dan:
QR = x + 1 = 14 + 1 = 15
PQ = x + 2 = 14 + 2 = 16
PS = 3x + 3 = 3*14 + 3 = 55
b.
P'Q' = 18,75(x + 2) / (x + 1)
Invullen x = 14 levert:
P'Q' = 20
Andere paragrafen:
2.1. Kruisproducten (1 t/m 16)
2.2. Gelijkvormigheid (17 t/m 26)
2.3. Gelijkvormige driehoeken (27 t/m 40)
2.4. Snavel- en zandloperfiguren (41 t/m 54)
2.1. Kruisproducten (1 t/m 16)
2.2. Gelijkvormigheid (17 t/m 26)
2.3. Gelijkvormige driehoeken (27 t/m 40)
2.4. Snavel- en zandloperfiguren (41 t/m 54)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


