TIP: Wil je ook toegang tot meer dan 16.500 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 2.2 Gelijkvormigheid HAVO 3
Boek: Getal & Ruimte - Gelijkvormigheid HAVO 3 (deel 1) opgaven 17 t/m 26, 2010Bij een vergroting van driehoek ABC met een vergrotingsfactor 2 krijgen we een nieuwe driehoek DEF.
ABC noemen we het origineel en DEF noemen we het beeld. Bij een vergroting zijn de driehoeken gelijkvormig en zijn de overeenkomstige hoeken gelijk.
Om de zijden te bepalen, stellen we een verhoudingstabel op.
ABC noemen we het origineel en DEF noemen we het beeld. Bij een vergroting zijn de driehoeken gelijkvormig en zijn de overeenkomstige hoeken gelijk.
Om de zijden te bepalen, stellen we een verhoudingstabel op.
17.
a. AC' = 6 en AB' = 3 dus de vergrotingsfactor = 2
b. CC' = 2 x BB' = 2 x 1,6 = 3,2
AC = 2 x AB = 2 x 2,4 = 4,8
BC = AC - AB = 4,8 - 2,4 = 2,4
c.
Ja, dit is een verhoudingstabel.
18.
b.
=>
PR = (16 x 32) / 36 = 14,2
QP = (16 x 24) / 36 = 10,7
19.
a. driehoek PQR ∼ driehoek STU
b.
=>
ST = (38 x 22) / 35 = 23,9
TU = (15 x 22) / 35 = 9,4
20.
a. driehoek KLM ∼ driehoek FHG
b.
=>
LM = (14 x 31) / 23 = 18,9
KM = (14 x 35) / 23 = 21,3
21.
b.
=>
BD = (15 x 34) / 19 = 26,8
EB = (28 x 34) / 19 = 50,1
22.
a.
QS2 = QR2 + RS2
QS2 = 122 + 52
QS2 = 169
QS = √169 = 13
b. driehoek PQT ∼ driehoek RQS
c.
=>
QT = (30 x 13) / 12 = 32,5
PT = (30 x 5) / 12 = 12,5
23.
b. driehoek ABC ∼ driehoek DEF
=>
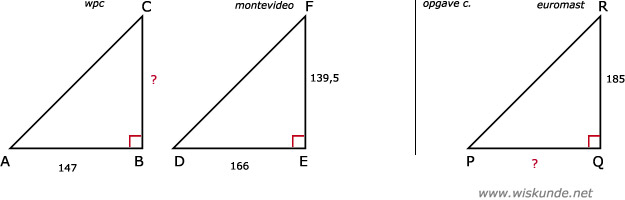
BC = (147 x 139,5) / 166 = 123,5
Dus de hoogte van WPC is 123,5 meter.
c.
driehoek DEF ∼ driehoek PQR
=>
PQ = (166 x 185) / 139,5 = 220,1
Dus de lengte van de schaduw van de euromast is 220,1 meter.
24.
b.
=>
TS = (5 x 8) / 12 = 3,3
PS = (5 x 7) / 12 = 2,9
25.
b.
DE2 + EF2 = DF2
DE2 + 122 = 202
DE2 = 400 - 144 = 256
DE = √256 = 16
c.
=>
GH = (5 x 12) / 16 = 3,75
DH = (5 x 20) / 16 = 6,25
d.
driehoek DEF ∼ driehoek KLF
=>
LF = (4 x 12) / 16 = 3
KF = (4 x 20) / 16 = 5
e.
HK = DF - DH - KF
HK = 20 - 6,25 - 5
HK = 8,75
26.
b.
=>
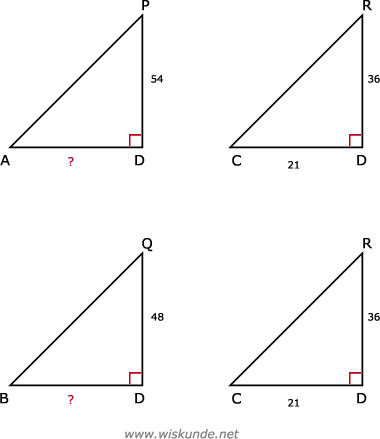
AD = (21 x 54) / 36 = 31,5
driehoek BDQ ∼ driehoek CDR
=>
BD = (21 x 48) / 36 = 28
c.
AB = AD - BD = 31,5 - 28 = 3,5
BC = AD - AB - CD = 31,5 - 3,5 - 21 = 7
a. AC' = 6 en AB' = 3 dus de vergrotingsfactor = 2
b. CC' = 2 x BB' = 2 x 1,6 = 3,2
AC = 2 x AB = 2 x 2,4 = 4,8
BC = AC - AB = 4,8 - 2,4 = 2,4
c.
| 2,4 | 1,6 | 3 |
| 4,8 | 3,2 | 6 |
18.
Tip:
'slangetje' betekent: is gelijkvormig met
a. driehoek ABC ∼ driehoek QRP'slangetje' betekent: is gelijkvormig met
b.
| driehoek ABC | AB | BC | AC |
| driehoek QRP | QR | PR | QP |
| 36 | 32 | 24 |
| 16 | PR | QP |
PR = (16 x 32) / 36 = 14,2
QP = (16 x 24) / 36 = 10,7
19.
a. driehoek PQR ∼ driehoek STU
b.
| driehoek PQR | PQ | QR | PR |
| driehoek STU | ST | TU | SU |
| 38 | 15 | 35 |
| ST | TU | 22 |
ST = (38 x 22) / 35 = 23,9
TU = (15 x 22) / 35 = 9,4
20.
a. driehoek KLM ∼ driehoek FHG
b.
| driehoek KLM | KL | LM | KM |
| driehoek FHG | FH | HG | FG |
| 14 | LM | KM |
| 23 | 31 | 35 |
LM = (14 x 31) / 23 = 18,9
KM = (14 x 35) / 23 = 21,3
21.
Tip:
Teken eerst driehoek ABC op een los blaadje. Teken daarnaast driehoek EBD alsof deze een juiste vergroting is van driehoek ABC. Op deze wijze kun je weer heel gemakkelijk de verhoudingstabel maken.
a. driehoek ABC ∼ driehoek EBDTeken eerst driehoek ABC op een los blaadje. Teken daarnaast driehoek EBD alsof deze een juiste vergroting is van driehoek ABC. Op deze wijze kun je weer heel gemakkelijk de verhoudingstabel maken.
b.
| driehoek ABC | AB | BC | AC |
| driehoek EBD | EB | BD | DE |
| 28 | 15 | 19 |
| EB | BD | 34 |
BD = (15 x 34) / 19 = 26,8
EB = (28 x 34) / 19 = 50,1
22.
a.
QS2 = QR2 + RS2
QS2 = 122 + 52
QS2 = 169
QS = √169 = 13
b. driehoek PQT ∼ driehoek RQS
c.
| driehoek PQT | PQ | QT | PT |
| driehoek RQS | RQ | QS | RS |
| 30 | QT | PT |
| 12 | 13 | 5 |
QT = (30 x 13) / 12 = 32,5
PT = (30 x 5) / 12 = 12,5
23.
Tip:
In een verhoudingstabel staat de langste zijde onder de langste zijde en de kortste zijde onder de kortste zijde.
a. Zie afbeeldingIn een verhoudingstabel staat de langste zijde onder de langste zijde en de kortste zijde onder de kortste zijde.
b. driehoek ABC ∼ driehoek DEF
| driehoek ABC | AB | BC | AC |
| driehoek DEF | DE | EF | DF |
| 147 | BC | AC |
| 166 | 139,5 | DF |
BC = (147 x 139,5) / 166 = 123,5
Dus de hoogte van WPC is 123,5 meter.
c.
driehoek DEF ∼ driehoek PQR
| driehoek DEF | DE | EF | DF |
| driehoek PQR | PQ | QR | PR |
| 166 | 139,5 | DF |
| PQ | 185 | PR |
PQ = (166 x 185) / 139,5 = 220,1
Dus de lengte van de schaduw van de euromast is 220,1 meter.

24.
Tip:
Je kunt ook de 2 driehoeken naast elkaar tekenen. Dan zie je het beter en kun je de verhoudingstabel beter maken.
a. driehoek PQR ∼ driehoek PTSJe kunt ook de 2 driehoeken naast elkaar tekenen. Dan zie je het beter en kun je de verhoudingstabel beter maken.
b.
| driehoek PQR | PQ | QR | PR |
| driehoek PTS | PT | TS | PS |
| 12 | 8 | 7 |
| 5 | TS | PS |
TS = (5 x 8) / 12 = 3,3
PS = (5 x 7) / 12 = 2,9
25.
Tip:
DE kun je berekenen met de Stelling van Pythagoras.
a. driehoek DEF ∼ driehoek DGH en driehoek DEF ∼ driehoek KLFDE kun je berekenen met de Stelling van Pythagoras.
b.
DE2 + EF2 = DF2
DE2 + 122 = 202
DE2 = 400 - 144 = 256
DE = √256 = 16
c.
| driehoek DEF | DE | EF | DF |
| driehoek DGH | DG | GH | DH |
| 16 | 12 | 20 |
| 5 | GH | DH |
GH = (5 x 12) / 16 = 3,75
DH = (5 x 20) / 16 = 6,25
d.
driehoek DEF ∼ driehoek KLF
| driehoek DEF | DE | EF | DF |
| driehoek KLF | KL | LF | KF |
| 16 | 12 | 20 |
| 4 | LF | KF |
LF = (4 x 12) / 16 = 3
KF = (4 x 20) / 16 = 5
e.
HK = DF - DH - KF
HK = 20 - 6,25 - 5
HK = 8,75
26.
Tip:
Van de rechthoekige driehoek CDR weet je 2 zijden (en dus altijd de 3e met Pythagoras) dus neem deze driehoek altijd mee in je berekeningen.
a. driehoek ADP ∼ driehoek BDQ en driehoek ADP ∼ driehoek CDRVan de rechthoekige driehoek CDR weet je 2 zijden (en dus altijd de 3e met Pythagoras) dus neem deze driehoek altijd mee in je berekeningen.
b.
| driehoek ADP | AD | DP | AP |
| driehoek CDR | CD | DR | CR |
| AD | 54 | AP |
| 21 | 36 | CR |
AD = (21 x 54) / 36 = 31,5
driehoek BDQ ∼ driehoek CDR
| driehoek BDQ | BD | DQ | BQ |
| driehoek CDR | CD | DR | CR |
| BD | 48 | BQ |
| 21 | 36 | CR |
BD = (21 x 48) / 36 = 28
c.
AB = AD - BD = 31,5 - 28 = 3,5
BC = AD - AB - CD = 31,5 - 3,5 - 21 = 7

Andere paragrafen:
2.1. Kruisproducten (1 t/m 16)
2.2. Gelijkvormigheid (17 t/m 26)
2.3. Gelijkvormige driehoeken (27 t/m 40)
2.4. Snavel- en zandloperfiguren (41 t/m 54)
2.1. Kruisproducten (1 t/m 16)
2.2. Gelijkvormigheid (17 t/m 26)
2.3. Gelijkvormige driehoeken (27 t/m 40)
2.4. Snavel- en zandloperfiguren (41 t/m 54)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


