TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 2.3 Gelijkvormige driehoeken HAVO 3
Boek: Getal & Ruimte - Gelijkvormigheid HAVO 3 (deel 1) opgaven 27 t/m 40, 2010Wat zijn gelijkvormige driehoeken?
Twee driehoeken zijn gelijkvormig als er 2 hoeken zijn in de ene driehoek die gelijk zijn met 2 hoeken in de andere driehoek.
Uiteraard volgt hieruit dat de derde hoeken van beide driehoeken dan ook gelijk moeten zijn.
Dus als we zeker weten dat 2 driehoeken 2 gelijke hoeken hebben dan kunnen we met een verhoudingstabel weer de diverse zijden uitrekenen.
Twee driehoeken zijn gelijkvormig als er 2 hoeken zijn in de ene driehoek die gelijk zijn met 2 hoeken in de andere driehoek.
Uiteraard volgt hieruit dat de derde hoeken van beide driehoeken dan ook gelijk moeten zijn.
Dus als we zeker weten dat 2 driehoeken 2 gelijke hoeken hebben dan kunnen we met een verhoudingstabel weer de diverse zijden uitrekenen.
27.
∠C = 180º - ∠A - ∠B = 180º - 80º - 30º = 70º
∠P = 180º - ∠Q - ∠R = 180º - 80º - 30º = 70º
Dus: ∠C = ∠P = 70º
28.
∠A1 = ∠A2
∠B = ∠E
(dus de 3e hoeken zijn ook gelijk!)
Hieruit volgt dat: driehoek ABC ∼ driehoek AED
b.
=>
AD = (8 x 3) / 6 = 4
ED = (8 x 4) / 6 = 5,3
CD = AD - AC = 4 - 3 = 1
29.
a.
∠Q1 = ∠Q2
∠R = ∠S
(dus de 3e hoeken zijn ook gelijk!)
Hieruit volgt dat: driehoek PQR ∼ driehoek TQS
b.
=>
PQ = (8 x 10) / 6 = 13,3
TS = (6 x 8) / 10 = 4,8
PT = PQ - TQ = 13,3 - 8 = 5,3
30.
∠A = ∠A
∠C1 = ∠D = 90º
(dus de 3e hoeken zijn ook gelijk!)
Hieruit volgt dat: driehoek ABC ∼ driehoek AED
b.
=>
AE = (5 x 9) / 4 = 11,25
AD = (3 x 9) / 4 = 6,75
31.
∠B = ∠B
(dus de 3e hoeken zijn ook gelijk: ∠C = ∠D)
Hieruit volgt dat: driehoek ABC ∼ driehoek EBD
=>
BC = (18 x 13) / 12 = 19,5
AC = (18 x 5) / 12 = 7,5
32.
∠S = ∠Q = 90º
(dus de 3e hoeken zijn ook gelijk: ∠T = ∠R)
Hieruit volgt dat: driehoek PST ∼ driehoek PQR
=>
PS = (24 x 12) / 30 = 9,6
ST = (18 x 12) / 30 = 7,2
∠R = ∠R
∠Q = ∠V = 90º
(dus de 3e hoeken zijn ook gelijk: ∠P = ∠U)
Hieruit volgt dat: driehoek PQR ∼ driehoek UVR
=>
VR = (4 x 18) / 24 = 3
UR = (4 x 30) / 24 = 5
TV = PR - PT - VR = 30 - 12 - 3 = 15
33.
∠F1 = ∠F2 (overstaande hoeken)
∠E = ∠H (i.v.m. Z-hoeken)
(dus de 3e hoeken zijn ook gelijk: ∠D = ∠G)
Hieruit volgt dat: driehoek EFD ∼ driehoek HFG
=>
FG = (4,2 x 2,6) / 1,4 = 7,8
HG = (4,2 x 2,2) / 1,4 = 6,6
b.
DG = DF + FG = 2,6 + 7,8 = 10,4
34.
∠B = ∠E1 (i.v.m. F-hoeken)
(dus de 3e hoeken zijn ook gelijk: ∠C = ∠C)
Hieruit volgt dat: driehoek ABC ∼ driehoek DEC
=>
AC = (30 x 24) / 20 = 36
AD = AC - CD = 36 - 24 = 12
BC = (30 x 21) / 20 = 31,5
BE = BC - CE = 31,5 - 21 = 10,5
35.
∠Q1 = ∠Q2 (overstaande hoeken)
(dus de 3e hoeken zijn ook gelijk: ∠T = ∠S)
Hieruit volgt dat: driehoek PQT ∼ driehoek RQS
=>
PT = (20 x 6) / 8 = 15
QT = (20 x 10) / 8 = 25
36.
∠D1 = ∠C (i.v.m. F-hoeken)
(dus de 3e hoeken zijn ook gelijk: ∠E1 = ∠B)
Hieruit volgt dat: driehoek AED ∼ driehoek ABC
=>
AB = (27 x 26) / 18 = 39
BC = (20 x 26) / 18 = 28,9
BE = AB - AE = 39 - 27 = 12
∠C = 180º - ∠A - ∠B = 180º - 80º - 30º = 70º
∠P = 180º - ∠Q - ∠R = 180º - 80º - 30º = 70º
Dus: ∠C = ∠P = 70º
28.
Tip:
Als driehoek ABC gelijkvormig is met driehoek DEF dan:
∠A = ∠D
∠B = ∠E
∠C = ∠F
a.Als driehoek ABC gelijkvormig is met driehoek DEF dan:
∠A = ∠D
∠B = ∠E
∠C = ∠F
∠A1 = ∠A2
∠B = ∠E
(dus de 3e hoeken zijn ook gelijk!)
Hieruit volgt dat: driehoek ABC ∼ driehoek AED
b.
| driehoek ABC | AB | BC | AC |
| driehoek AED | AE | ED | AD |
| 6 | 4 | 3 |
| 8 | ED | AD |
AD = (8 x 3) / 6 = 4
ED = (8 x 4) / 6 = 5,3
CD = AD - AC = 4 - 3 = 1
29.
a.
∠Q1 = ∠Q2
∠R = ∠S
(dus de 3e hoeken zijn ook gelijk!)
Hieruit volgt dat: driehoek PQR ∼ driehoek TQS
b.
| driehoek PQR | PQ | QR | PR |
| driehoek TQS | TQ | QS | TS |
| PQ | 10 | 8 |
| 8 | 6 | TS |
PQ = (8 x 10) / 6 = 13,3
TS = (6 x 8) / 10 = 4,8
PT = PQ - TQ = 13,3 - 8 = 5,3
30.
Tip:
Bereken AB met de Stelling van Pythagoras: AC2 + BC2 = AB2
AB = 5
a.Bereken AB met de Stelling van Pythagoras: AC2 + BC2 = AB2
AB = 5
∠A = ∠A
∠C1 = ∠D = 90º
(dus de 3e hoeken zijn ook gelijk!)
Hieruit volgt dat: driehoek ABC ∼ driehoek AED
b.
| driehoek ABC | AB | BC | AC |
| driehoek AED | AE | ED | AD |
| 5 | 4 | 3 |
| AE | 9 | AD |
AE = (5 x 9) / 4 = 11,25
AD = (3 x 9) / 4 = 6,75
31.
Tip:
Bereken BE met de Stelling van Pythagoras: BE2 + DE2 = BD2
BE = 12
∠A = ∠E = 90ºBereken BE met de Stelling van Pythagoras: BE2 + DE2 = BD2
BE = 12
∠B = ∠B
(dus de 3e hoeken zijn ook gelijk: ∠C = ∠D)
Hieruit volgt dat: driehoek ABC ∼ driehoek EBD
| driehoek ABC | AB | BC | AC |
| driehoek EBD | EB | BD | ED |
| 18 | BC | AC |
| 12 | 13 | 5 |
BC = (18 x 13) / 12 = 19,5
AC = (18 x 5) / 12 = 7,5
32.
Tip:
Bereken PR met de Stelling van Pythagoras: PQ2 + QR2 = PR2
PR = 30
∠P = ∠PBereken PR met de Stelling van Pythagoras: PQ2 + QR2 = PR2
PR = 30
∠S = ∠Q = 90º
(dus de 3e hoeken zijn ook gelijk: ∠T = ∠R)
Hieruit volgt dat: driehoek PST ∼ driehoek PQR
| driehoek PST | PS | ST | PT |
| driehoek PQR | PQ | QR | PR |
| PS | ST | 12 |
| 24 | 18 | 30 |
PS = (24 x 12) / 30 = 9,6
ST = (18 x 12) / 30 = 7,2
∠R = ∠R
∠Q = ∠V = 90º
(dus de 3e hoeken zijn ook gelijk: ∠P = ∠U)
Hieruit volgt dat: driehoek PQR ∼ driehoek UVR
| driehoek PQR | PQ | QR | PR |
| driehoek UVR | UV | VR | UR |
| 24 | 18 | 30 |
| 4 | VR | UR |
VR = (4 x 18) / 24 = 3
UR = (4 x 30) / 24 = 5
TV = PR - PT - VR = 30 - 12 - 3 = 15
33.
Tip:
Omdat DE evenwijdig is met HG vormt D-E-F-H-G een Z-hoek.
Dus ∠DEF = ∠FHG
a.Omdat DE evenwijdig is met HG vormt D-E-F-H-G een Z-hoek.
Dus ∠DEF = ∠FHG
∠F1 = ∠F2 (overstaande hoeken)
∠E = ∠H (i.v.m. Z-hoeken)
(dus de 3e hoeken zijn ook gelijk: ∠D = ∠G)
Hieruit volgt dat: driehoek EFD ∼ driehoek HFG
| driehoek EFD | EF | FD | ED |
| driehoek HFG | HF | FG | HG |
| 1,4 | 2,6 | 2,2 |
| 4,2 | FG | HG |
FG = (4,2 x 2,6) / 1,4 = 7,8
HG = (4,2 x 2,2) / 1,4 = 6,6
b.
DG = DF + FG = 2,6 + 7,8 = 10,4
34.
Tip:
Zoek de F-hoeken
∠A = ∠D1 (i.v.m. F-hoeken)Zoek de F-hoeken
∠B = ∠E1 (i.v.m. F-hoeken)
(dus de 3e hoeken zijn ook gelijk: ∠C = ∠C)
Hieruit volgt dat: driehoek ABC ∼ driehoek DEC
| driehoek ABC | AB | BC | AC |
| driehoek DEC | DE | EC | DC |
| 30 | BC | AC |
| 20 | 21 | 24 |
AC = (30 x 24) / 20 = 36
AD = AC - CD = 36 - 24 = 12
BC = (30 x 21) / 20 = 31,5
BE = BC - CE = 31,5 - 21 = 10,5
35.
Tip:
Bereken QS met de Stelling van Pythagoras: QR2 + RS2 = QS2
QS = 10
∠P = ∠R = 90ºBereken QS met de Stelling van Pythagoras: QR2 + RS2 = QS2
QS = 10
∠Q1 = ∠Q2 (overstaande hoeken)
(dus de 3e hoeken zijn ook gelijk: ∠T = ∠S)
Hieruit volgt dat: driehoek PQT ∼ driehoek RQS
| driehoek PQT | PQ | QT | PT |
| driehoek RQS | RQ | QS | RS |
| 20 | QT | PT |
| 8 | 10 | 6 |
PT = (20 x 6) / 8 = 15
QT = (20 x 10) / 8 = 25
36.
Tip:
Maak gebruik van F-hoeken om gelijkvormigheid aan te tonen.
∠A = ∠A (in de 2 verschillende driehoeken)Maak gebruik van F-hoeken om gelijkvormigheid aan te tonen.
∠D1 = ∠C (i.v.m. F-hoeken)
(dus de 3e hoeken zijn ook gelijk: ∠E1 = ∠B)
Hieruit volgt dat: driehoek AED ∼ driehoek ABC
| driehoek AED | AE | ED | AD |
| driehoek ABC | AB | BC | AC |
| 27 | 20 | 18 |
| AB | BC | 26 |
AB = (27 x 26) / 18 = 39
BC = (20 x 26) / 18 = 28,9
BE = AB - AE = 39 - 27 = 12
37.
Driehoek ABC ∼ driehoek PQR want:
∠A = ∠P = 90º
∠B = ∠Q (i.v.m. F-hoeken)
(dus de 3e hoeken zijn ook gelijk: ∠C = ∠R)
Hieruit volgt dat: driehoek ABC ∼ driehoek PQR
b.
=>
c.
AC = (14,5 x 1,5) / 1,1 = 19,77
Dus de hoogte van het gebouw is 19,8 meter.
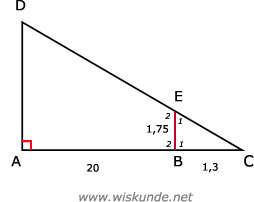
38.
∠A = ∠B1 = 90º
∠C = ∠C
(dus de 3e hoeken zijn ook gelijk: ∠D = ∠E1)
Hieruit volgt dat: driehoek ACD ∼ driehoek BCE
=>
AD = (21,3 x 1,75) / 1,3 = 28,7
Dus de hoogte van de boom is 28,7 meter.
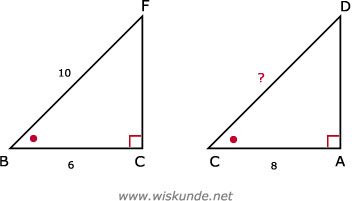
39.
∠B = ∠C (gegeven rood bolletje)
∠C = ∠A (90º
(dus de 3e hoeken zijn ook gelijk: ∠F = ∠D)
Hieruit volgt dat: driehoek BCF ∼ driehoek CAD
=>
CD = (10 x 8) / 6 = 13,3
Dus de lengte ladder CD is 13,3 meter.
40.
∠F = ∠E (90 graden)
∠FDA = ∠BAE
(dus de 3e hoeken zijn ook gelijk)
Hieruit volgt dat: driehoek ADF ∼ driehoek BAE
=>
AF = (1,2 x 1,5) / 2,5 = 0,72
Pythagoras:
AF2 + DF2 = AD2
DF2 = 0,9216
DF = √0,9216 = 0,96 m
Dus de hoogte van punt D is 96 cm.
b. C is 2,46 meter.
Tip:
Maak eventueel een schets van de situatie. Dan zie je het misschien beter. De hoeken bij B en Q vormen een F-hoek.
a.Maak eventueel een schets van de situatie. Dan zie je het misschien beter. De hoeken bij B en Q vormen een F-hoek.
Driehoek ABC ∼ driehoek PQR want:
∠A = ∠P = 90º
∠B = ∠Q (i.v.m. F-hoeken)
(dus de 3e hoeken zijn ook gelijk: ∠C = ∠R)
Hieruit volgt dat: driehoek ABC ∼ driehoek PQR
b.
| driehoek ABC | AB | BC | AC |
| driehoek PQR | PQ | QR | PR |
| 14,5 | BC | AC |
| 1,1 | QR | 1,5 |
c.
AC = (14,5 x 1,5) / 1,1 = 19,77
Dus de hoogte van het gebouw is 19,8 meter.
38.
Tip:
∠D = ∠E1 vanwege een F-hoek
Driehoek ACD ∼ driehoek BCE want:∠D = ∠E1 vanwege een F-hoek
∠A = ∠B1 = 90º
∠C = ∠C
(dus de 3e hoeken zijn ook gelijk: ∠D = ∠E1)
Hieruit volgt dat: driehoek ACD ∼ driehoek BCE
| driehoek ACD | AC | CD | AD |
| driehoek BCE | BC | CE | BE |
| 21,3 | CD | AD |
| 1,3 | CE | 1,75 |
AD = (21,3 x 1,75) / 1,3 = 28,7
Dus de hoogte van de boom is 28,7 meter.

39.
Tip:
Leer momentje: Driehoek BEC is gelijkbenig omdat de basishoeken gelijk zijn. Dus BE = CE.
Driehoek BCF ∼ driehoek CAD want:Leer momentje: Driehoek BEC is gelijkbenig omdat de basishoeken gelijk zijn. Dus BE = CE.
∠B = ∠C (gegeven rood bolletje)
∠C = ∠A (90º
(dus de 3e hoeken zijn ook gelijk: ∠F = ∠D)
Hieruit volgt dat: driehoek BCF ∼ driehoek CAD
| driehoek BCF | BC | CF | BF |
| driehoek CAD | CA | AD | CD |
| 6 | CF | 10 |
| 8 | AD | CD |
CD = (10 x 8) / 6 = 13,3
Dus de lengte ladder CD is 13,3 meter.

40.
Tip:
Bereken eerst AF en dan DF met de stelling van Pythagoras. Als je DF weet, weet je ook de hoogte van D.
Driehoek ADF ∼ driehoek BAE want:Bereken eerst AF en dan DF met de stelling van Pythagoras. Als je DF weet, weet je ook de hoogte van D.
∠F = ∠E (90 graden)
∠FDA = ∠BAE
(dus de 3e hoeken zijn ook gelijk)
Hieruit volgt dat: driehoek ADF ∼ driehoek BAE
| driehoek ADF | AD | DF | AF |
| driehoek BAE | BA | AE | BE |
| 1,2 | DF | AF |
| 2,5 | AE | 1,5 |
AF = (1,2 x 1,5) / 2,5 = 0,72
Pythagoras:
AF2 + DF2 = AD2
DF2 = 0,9216
DF = √0,9216 = 0,96 m
Dus de hoogte van punt D is 96 cm.
b. C is 2,46 meter.
Andere paragrafen:
2.1. Kruisproducten (1 t/m 16)
2.2. Gelijkvormigheid (17 t/m 26)
2.3. Gelijkvormige driehoeken (27 t/m 40)
2.4. Snavel- en zandloperfiguren (41 t/m 54)
2.1. Kruisproducten (1 t/m 16)
2.2. Gelijkvormigheid (17 t/m 26)
2.3. Gelijkvormige driehoeken (27 t/m 40)
2.4. Snavel- en zandloperfiguren (41 t/m 54)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


