TIP: Wil je ook toegang tot meer dan 16.500 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 2.4 Snavel- en zandloperfiguren HAVO 3
Boek: Getal & Ruimte - Gelijkvormigheid HAVO 3 (deel 1) opgaven 41 t/m 54, 2010Bij gelijkvormige driehoeken maken we gebruik van snavelfiguren en zandloperfiguren.
Deze bestaan alleen als er evenwijdige lijnen zijn. Deze worden aangegeven met pijltjes.
Bij snavelfiguren kunnen we F-hoeken onderscheiden en bij zandloperfiguren kunnen we Z-hoeken vinden.
Op deze wijze maken we weer gebruik van een verhoudingstabel.
Deze bestaan alleen als er evenwijdige lijnen zijn. Deze worden aangegeven met pijltjes.
Bij snavelfiguren kunnen we F-hoeken onderscheiden en bij zandloperfiguren kunnen we Z-hoeken vinden.
Op deze wijze maken we weer gebruik van een verhoudingstabel.
41.
Driehoek BEF ∼ driehoek AED en driehoek BEF ∼ driehoek CDF
42.
=>
b.
PQ = (3,5 x 3) / 1,5 = 7
PR = (3,5 x 2,4) / 1,5 = 5,6
43.
=>
b.
BC = (7 x 2) / 3 = 4,7
CE = (3 x 4) / 7 = 1,7
44.
a.
b.
EG = (14 x 38) / 30 = 17,73
BD = (5 x 38) / 18 = 10,56
CD = (5 x 30) / 18 = 8,33
FG = (18 x 14) / 30 = 8,40
45.
b.
AQ = (12 x 3) / 9 = 4
46.
b.
CQ = (2 x 4) / 3 = 8 / 3 ≈ 2,7
47.
a.
=>
PC = (8 x 3) / 7 = 24 / 7 ≈ 3,43
b.
Omdat ∠B recht is, geldt:
AB2 + BQ2 = AQ2
AQ2 = 113
AQ = √113
Bereken nu PQ met de Stelling van Pythagoras:
PC2 + CQ2 = PQ2
(3,43)2 + 32 = PQ2
PQ2 = 20,755
PQ = 4,56
AP = AQ - PQ
AP = √113 - 4,56
AP ≈ 6,07
48.
=>
BF = (1,5 x 3) / 2 = 2,25
49.
Zie afbeelding a:
=>
AC = (7 x 1,6) / 2 = 5,6
Dus de hoogte van de lantaarnpalen is 5,6 meter.
b.
Zie afbeelding b:
=>
AB = (5 x 5,6) / 1,6 = 17,5
Dus de afstand tussen de lantaarnpalen is 17,5 meter.
50.
2(x + 6) = 9x
2x + 12 = 9x
-7x = -12
x = 12/7
x ≈ 1,7 meter
b.
2,5(y + 3,5) = 3,5 x 9
2,5y + 8,75 = 31,5
2,5y = 22,75
y = 9,1
Driehoek BEF ∼ driehoek AED en driehoek BEF ∼ driehoek CDF
42.
Tip:
ST is evenwijdig met PQ dus daarom weten we zeker dat er sprake is van een snavelfiguur (F-hoeken).
a.ST is evenwijdig met PQ dus daarom weten we zeker dat er sprake is van een snavelfiguur (F-hoeken).
| PQ | QR | PR |
| ST | TR | SR |
| PQ | 3,5 | PR |
| 3 | 1,5 | 2,4 |
b.
PQ = (3,5 x 3) / 1,5 = 7
PR = (3,5 x 2,4) / 1,5 = 5,6
43.
Tip:
DE is evenwijdig met AB dus daarom weten we zeker dat er sprake is van een zandloperfiguur (Z-hoeken).
a.DE is evenwijdig met AB dus daarom weten we zeker dat er sprake is van een zandloperfiguur (Z-hoeken).
| AB | BC | AC |
| DE | CD | CE |
| 7 | BC | 4 |
| 3 | 2 | CE |
b.
BC = (7 x 2) / 3 = 4,7
CE = (3 x 4) / 7 = 1,7
44.
a.
| Zandloper: | ||||||||||||||
|
=> |
|
||||||||||||
| Snavel: | ||||||||||||||
|
=> |
|
||||||||||||
b.
EG = (14 x 38) / 30 = 17,73
BD = (5 x 38) / 18 = 10,56
CD = (5 x 30) / 18 = 8,33
FG = (18 x 14) / 30 = 8,40
45.
Tip:
Omdat er sprake is van een parallellogram geldt dat DC evenwijdig is aan AB.
Op basis van evenwijdigheid kunnen we een snavel- en/of een zandloperfiguur ontdekken.
a.Omdat er sprake is van een parallellogram geldt dat DC evenwijdig is aan AB.
Op basis van evenwijdigheid kunnen we een snavel- en/of een zandloperfiguur ontdekken.
| AQ | AP |
| DC | DP |
| AQ | 3 |
| 12 | 9 |
AQ = (12 x 3) / 9 = 4
46.
Tip:
PC = AB - DP = 5 - 3 = 2
a.PC = AB - DP = 5 - 3 = 2
| CQ | PC | PQ |
| AD | DP | AP |
| CQ | 2 |
| 4 | 3 |
CQ = (2 x 4) / 3 = 8 / 3 ≈ 2,7
47.
Tip:
Omdat ABCD een rechthoek is, weten we zeker dat PC evenwijdig is met AB. Hierdoor is er sprake van een snavelfiguur.
Ook is er sprake van een zandloperfiguur. Probeer beide en kijk welke lukt.
De snavelbek lukt:Omdat ABCD een rechthoek is, weten we zeker dat PC evenwijdig is met AB. Hierdoor is er sprake van een snavelfiguur.
Ook is er sprake van een zandloperfiguur. Probeer beide en kijk welke lukt.
a.
| PC | CQ | PQ |
| AB | BQ | AQ |
| PC | 3 | PQ |
| 8 | 7 | AQ |
PC = (8 x 3) / 7 = 24 / 7 ≈ 3,43
b.
Omdat ∠B recht is, geldt:
AB2 + BQ2 = AQ2
AQ2 = 113
AQ = √113
Bereken nu PQ met de Stelling van Pythagoras:
PC2 + CQ2 = PQ2
(3,43)2 + 32 = PQ2
PQ2 = 20,755
PQ = 4,56
AP = AQ - PQ
AP = √113 - 4,56
AP ≈ 6,07
48.
Tip:
Omdat ABCD een parallellogram is, geldt dat DE is evenwijdig met BC. Hieruit volgt ook dat AE evenwijdig is met BC. Dus we hebben een zandloper gevonden.
Tevens: BC = AD = 3
Omdat ABCD een parallellogram is, geldt dat DE is evenwijdig met BC. Hieruit volgt ook dat AE evenwijdig is met BC. Dus we hebben een zandloper gevonden.
Tevens: BC = AD = 3
| AE | AF | EF |
| BC | BF | CF |
| 2 | 1,5 | EF |
| 3 | BF | CF |
BF = (1,5 x 3) / 2 = 2,25
49.
Tip:
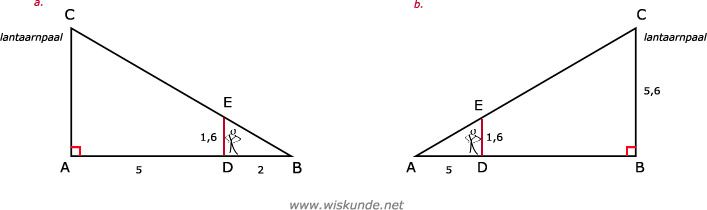
Er is sprake van een snavelfiguur omdat de lantaarn en het mannetje evenwijdig zijn.
AC en DE zijn dus evenwijdig (bij opgave a.). Bij opgave b. geldt hetzelfde.
a.Er is sprake van een snavelfiguur omdat de lantaarn en het mannetje evenwijdig zijn.
AC en DE zijn dus evenwijdig (bij opgave a.). Bij opgave b. geldt hetzelfde.
Zie afbeelding a:
| AB | BC | AC |
| DB | BE | DE |
| 7 | BC | AC |
| 2 | BE | 1,6 |
AC = (7 x 1,6) / 2 = 5,6
Dus de hoogte van de lantaarnpalen is 5,6 meter.
b.
Zie afbeelding b:
| AD | DE | AE |
| AB | BC | AC |
| 5 | 1,6 | AE |
| AB | 5,6 | AC |
AB = (5 x 5,6) / 1,6 = 17,5
Dus de afstand tussen de lantaarnpalen is 17,5 meter.

50.
Tip:
Werk het kruisproduct uit.
a.Werk het kruisproduct uit.
2(x + 6) = 9x
2x + 12 = 9x
-7x = -12
x = 12/7
x ≈ 1,7 meter
b.
| 3,5 | 2,5 |
| y + 3,5 | 9 |
2,5(y + 3,5) = 3,5 x 9
2,5y + 8,75 = 31,5
2,5y = 22,75
y = 9,1
51.
Zie afbeelding
52.
=>
AP = (3 x 3) / 2 = 4,5
b. Snavel:
=>
CS = (2,5 x 5) / 5,5 ≈ 2,27
53.
=>
AP = (6 x 2) / 4 = 3
b. Snavel:
=>
CL = (2 x 6) / 8 = 12/8 = 1,5
54.
=>
AQ = (3 x 4) / 5 = 12/5 = 2,4
b. Zandloper:
=>
BS = (3 x 2) / 4 = 6/4 = 1,5
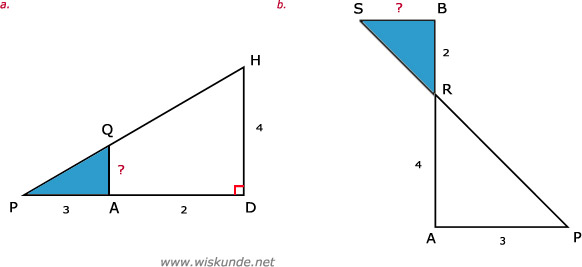
Zie afbeelding

52.
Tip:
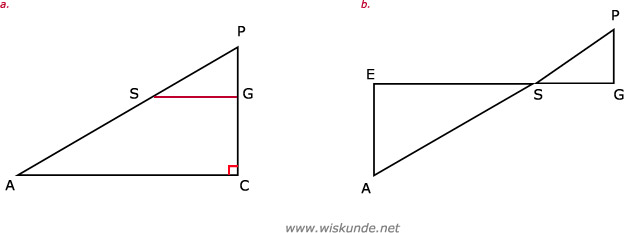
Je ziet zowel een snavelfiguur als een zandloperfiguur. Bekijk steeds welke van de twee wel lukt.
EQ = AE - AQ = 5 - 3 = 2
a. Zandloper:Je ziet zowel een snavelfiguur als een zandloperfiguur. Bekijk steeds welke van de twee wel lukt.
EQ = AE - AQ = 5 - 3 = 2
| AP | AQ | PQ |
| EH | EQ | HQ |
| AP | 3 | PQ |
| 3 | 2 | HQ |
AP = (3 x 3) / 2 = 4,5
b. Snavel:
| BR | RF | BF |
| CR | RS | CS |
| 5,5 | RF | 5 |
| 2,5 | RS | CS |
CS = (2,5 x 5) / 5,5 ≈ 2,27

53.
Tip:
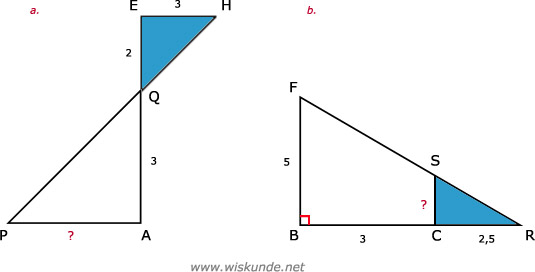
Bedenk dat de afbeeldingen schetsen zijn. Dus de afmetingen hoeven niet te kloppen.
EK = 6 - 2 = 4
a. Zandloper:Bedenk dat de afbeeldingen schetsen zijn. Dus de afmetingen hoeven niet te kloppen.
EK = 6 - 2 = 4
| AP | AK | PK |
| EH | EK | HK |
| AP | 2 | PK |
| 6 | 4 | HK |
AP = (6 x 2) / 4 = 3
b. Snavel:
| CQ | LQ | CL |
| DQ | HQ | DH |
| 2 | LQ | CL |
| 8 | HQ | 6 |
CL = (2 x 6) / 8 = 12/8 = 1,5

54.
Tip:
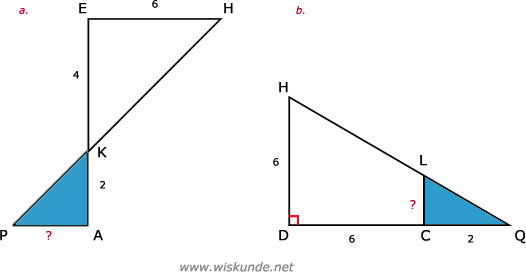
BR = AB - AR = 6 - 4 = 2
a. Snavel:BR = AB - AR = 6 - 4 = 2
| AP | AQ | PQ |
| DP | DH | HP |
| 3 | AQ | PQ |
| 5 | 4 | HP |
AQ = (3 x 4) / 5 = 12/5 = 2,4
b. Zandloper:
| AP | PR | AR |
| BS | RS | BR |
| 3 | PR | 4 |
| BS | RS | 2 |
BS = (3 x 2) / 4 = 6/4 = 1,5

Andere paragrafen:
2.1. Kruisproducten (1 t/m 16)
2.2. Gelijkvormigheid (17 t/m 26)
2.3. Gelijkvormige driehoeken (27 t/m 40)
2.4. Snavel- en zandloperfiguren (41 t/m 54)
2.1. Kruisproducten (1 t/m 16)
2.2. Gelijkvormigheid (17 t/m 26)
2.3. Gelijkvormige driehoeken (27 t/m 40)
2.4. Snavel- en zandloperfiguren (41 t/m 54)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


