TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 2.5 De oppervlakte van een driehoek HAVO/VWO 2
Boek: Getal & Ruimte - Vlakke figuren HAVO/VWO 2 (deel 1) opgaven 45 t/m 58, 2013, 10e editie
45.
a. opp(ABDE) = 4 x 3 = 12 cm2
b. opp(ABDE) = opp(AFCE)) + opp(FBDC)
Nu links en rechts x 1/2 levert:
1/2 x opp(ABDE) = 1/2 x opp(AFCE)) + 1/2 x opp(FBDC)
1/2 x opp(ABDE) = opp(AFC) + opp(FBC)
1/2 x opp(ABDE) = opp(ABC)
46.
b. oppervlakte EFG = 1/2 x basis x hoogte = 1/2 x FG x EH = 1/2 x 28 x 24 = 336 mm2
c. oppervlakte KLM = 1/2 x basis x hoogte = 1/2 x LM x KN = 1/2 x 42 x 16 = 336 mm2
47.
b. oppervlakte STU = 1/2 x basis x hoogte = 1/2 x TU x SU = 1/2 x 28 x 21 = 294 mm2
48.
a. Zie afbeelding
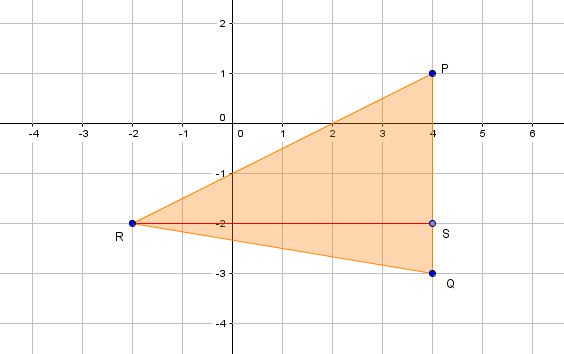
b. Het rode lijnstuk is de hoogtelijn RS uit punt R op basis PQ.
c. PQ = 4 cm en RS = 6 cm
d. oppervlakte PQR = 1/2 x basis x hoogte = 1/2 x PQ x RS = 1/2 x 4 x 6 = 12 cm2
49.
50.
a.
opp(DBC) = 10 cm2
opp(DAC) = 4 cm2
opp(ABC) = 10 - 4 = 6 cm2
b. 1/2 x AB x CD = 1/2 x 3 x 4 = 6 cm2, de uitkomsten zijn gelijk
c. CD
51.
b. oppervlakte driehoek PQR = 1/2 x zijde x bijbehorende hoogte = 1/2 x 4 x 4 = 8 cm2
c. oppervlakte driehoek OPQ = 1/2 x zijde x bijbehorende hoogte = 1/2 x 4 x 3 = 6 cm2
d. oppervlakte driehoek QRS = 1/2 x zijde x bijbehorende hoogte = 1/2 x 4 x 3 = 6 cm2
52.
oppervlakte driehoek I = 1/2 x 2 x 3 = 3 cm2
oppervlakte driehoek II = 1/2 x 3 x 2 = 3 cm2
oppervlakte driehoek III = 1/2 x 5 x 1 = 2,5 cm2
oppervlakte driehoek IV = 1/2 x 4 x 3 = 6 cm2
oppervlakte driehoek V = 1/2 x 1 x 3 = 1,5 cm2
oppervlakte driehoek VI = 1/2 x 3 x 2 = 3 cm2
oppervlakte driehoek VII = 1/2 x 2 x 3 = 3 cm2
53.
b. Zie afbeelding
c. *
54.
Maten gemeten in boek: basis = 5 cm en hoogte = 2,7 cm.
Oppervlakte driehoek ABC = 1/2 x basis x hoogte = 1/2 x AB x CD = 1/2 x 5 x 2,7 = 6,75 cm2
a. opp(ABDE) = 4 x 3 = 12 cm2
b. opp(ABDE) = opp(AFCE)) + opp(FBDC)
Nu links en rechts x 1/2 levert:
1/2 x opp(ABDE) = 1/2 x opp(AFCE)) + 1/2 x opp(FBDC)
1/2 x opp(ABDE) = opp(AFC) + opp(FBC)
1/2 x opp(ABDE) = opp(ABC)
46.
Tip:
oppervlakte driehoek = 1/2 x basis x hoogte
a. oppervlakte ABC = 1/2 x basis x hoogte = 1/2 x AB x CD = 1/2 x 28 x 15 = 210 mm2oppervlakte driehoek = 1/2 x basis x hoogte
b. oppervlakte EFG = 1/2 x basis x hoogte = 1/2 x FG x EH = 1/2 x 28 x 24 = 336 mm2
c. oppervlakte KLM = 1/2 x basis x hoogte = 1/2 x LM x KN = 1/2 x 42 x 16 = 336 mm2
47.
Tip:
De hoogte van een driehoek staat altijd loodrecht op de basis.
a. oppervlakte PQR = 1/2 x basis x hoogte = 1/2 x PQ x QR = 1/2 x 36 x 15 = 270 mm2De hoogte van een driehoek staat altijd loodrecht op de basis.
b. oppervlakte STU = 1/2 x basis x hoogte = 1/2 x TU x SU = 1/2 x 28 x 21 = 294 mm2
48.
a. Zie afbeelding
b. Het rode lijnstuk is de hoogtelijn RS uit punt R op basis PQ.
c. PQ = 4 cm en RS = 6 cm
d. oppervlakte PQR = 1/2 x basis x hoogte = 1/2 x PQ x RS = 1/2 x 4 x 6 = 12 cm2

49.
Tip:
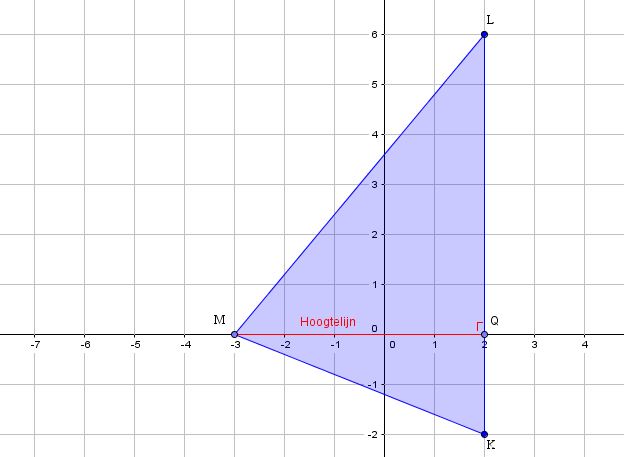
Trek de hoogtelijn uit M op KL. Met deze rode hoogtelijn MQ kun je hokjes tellen voor de lengte. De lengte van de hoogtelijn uit K is veel lastiger te bepalen. Dus kies slim!
Oppervlakte KLM = 1/2 x basis x hoogte = 1/2 x KL x MQ = 1/2 x 8 x 5 = 20 cm2
Trek de hoogtelijn uit M op KL. Met deze rode hoogtelijn MQ kun je hokjes tellen voor de lengte. De lengte van de hoogtelijn uit K is veel lastiger te bepalen. Dus kies slim!

50.
a.
opp(DBC) = 10 cm2
opp(DAC) = 4 cm2
opp(ABC) = 10 - 4 = 6 cm2
b. 1/2 x AB x CD = 1/2 x 3 x 4 = 6 cm2, de uitkomsten zijn gelijk
c. CD
51.
Tip:
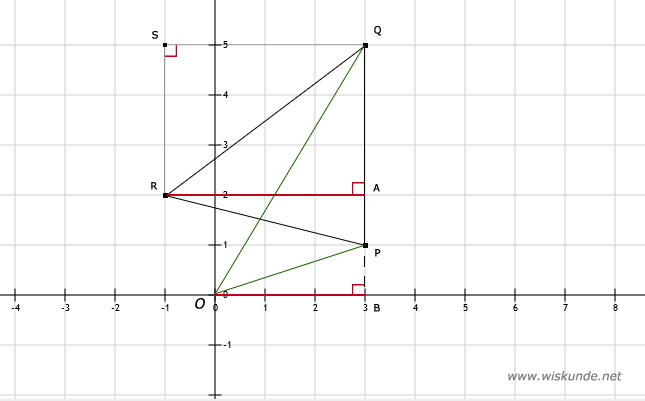
De bijbehorende hoogte van driehoek PQR is AR.
De bijbehorende hoogte van driehoek OPQ is OB.
a. Zie afbeeldingDe bijbehorende hoogte van driehoek PQR is AR.
De bijbehorende hoogte van driehoek OPQ is OB.
b. oppervlakte driehoek PQR = 1/2 x zijde x bijbehorende hoogte = 1/2 x 4 x 4 = 8 cm2
c. oppervlakte driehoek OPQ = 1/2 x zijde x bijbehorende hoogte = 1/2 x 4 x 3 = 6 cm2
d. oppervlakte driehoek QRS = 1/2 x zijde x bijbehorende hoogte = 1/2 x 4 x 3 = 6 cm2

52.
oppervlakte driehoek I = 1/2 x 2 x 3 = 3 cm2
oppervlakte driehoek II = 1/2 x 3 x 2 = 3 cm2
oppervlakte driehoek III = 1/2 x 5 x 1 = 2,5 cm2
oppervlakte driehoek IV = 1/2 x 4 x 3 = 6 cm2
oppervlakte driehoek V = 1/2 x 1 x 3 = 1,5 cm2
oppervlakte driehoek VI = 1/2 x 3 x 2 = 3 cm2
oppervlakte driehoek VII = 1/2 x 2 x 3 = 3 cm2
53.
Tip:
Bekijk van welke zijde en bijbehorende hoogte je de maten weet om zo de oppervlakte te bepalen.
a. opp(ABC) = 1/2 x zijde x bijbehorende hoogte = 1/2 x BC x AD = 1/2 x 20 x 24 = 240 mm2Bekijk van welke zijde en bijbehorende hoogte je de maten weet om zo de oppervlakte te bepalen.
b. Zie afbeelding
c. *

54.
Maten gemeten in boek: basis = 5 cm en hoogte = 2,7 cm.
Oppervlakte driehoek ABC = 1/2 x basis x hoogte = 1/2 x AB x CD = 1/2 x 5 x 2,7 = 6,75 cm2
55.
opp(ABC) = 1/2 x 8 x 3 = 12 m2
Dus er moet 2 x 12 = 24 m2 geschilderd worden.
Daar doet de schilder dus 24 / 3 = 8 uur over.
56.
Maten gemeten in boek: basis = 2 cm en hoogte = 4,6 cm.
Oppervlakte driehoek ABC = 1/2 x basis x hoogte = 1/2 x 2 x 4,6 = 4,6 m2
b. Verschil: 5,1 m2 - 4,6 m2 = 0,5 m2
57.
Oppervlakte grondzeil = lengte x breedte = 2 x 1 = 2 m2
b.
opp(voorkant / driehoek) = 1/2 x basis x hoogte = 1/2 x 1 x 1,2 = 0,6 m2
opp(achterkant / driehoek) = 1/2 x basis x hoogte = 1/2 x 1 x 1,2 = 0,6 m2
opp(rechthoek voor) = lengte x breedte = 2 x 1,3 = 2,6 m2
opp(rechthoek achter) = lengte x breedte = 2 x 1,3 = 2,6 m2
opp(grondzeil) = 2 m2
Totale oppervlakte van de hele tent: 8,4 m2
58.
oppervlakte driehoek links 1 = 1/2 x basis x hoogte = 1/2 x 30 x 80 = 1200 cm2
oppervlakte driehoek links 2 = 1/2 x basis x hoogte = 1/2 x 110 x 25 = 1375 cm2
2 x (1200 + 1375) = 5150 cm2
b. 4000 cm2
Tip:
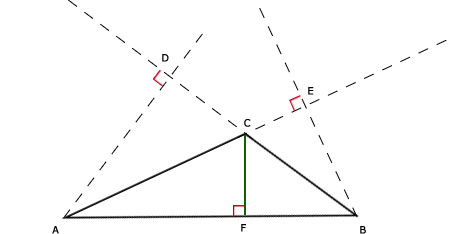
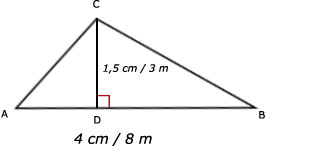
Maak een schets van de driehoek ABC met zijde AB = 4 cm en hoogte CD = 1,5 cm.
Gegeven is schaal 1 : 200. Dat betekent 1 cm in de tekening is 2 m in het echt (200 cm).
Dus 4 cm in het klein, is 8 m in het groot.
Afmetingen van de driehoek in het echt: zijde AB = 8 m en hoogte CD = 3 m.Maak een schets van de driehoek ABC met zijde AB = 4 cm en hoogte CD = 1,5 cm.
Gegeven is schaal 1 : 200. Dat betekent 1 cm in de tekening is 2 m in het echt (200 cm).
Dus 4 cm in het klein, is 8 m in het groot.
opp(ABC) = 1/2 x 8 x 3 = 12 m2
Dus er moet 2 x 12 = 24 m2 geschilderd worden.
Daar doet de schilder dus 24 / 3 = 8 uur over.

56.
Tip:
Schaal 1:100 d.w.z. dat 1 cm in het klein is gelijk aan 100 cm (= 1 meter) in het echt.
a.Schaal 1:100 d.w.z. dat 1 cm in het klein is gelijk aan 100 cm (= 1 meter) in het echt.
Maten gemeten in boek: basis = 2 cm en hoogte = 4,6 cm.
Oppervlakte driehoek ABC = 1/2 x basis x hoogte = 1/2 x 2 x 4,6 = 4,6 m2
b. Verschil: 5,1 m2 - 4,6 m2 = 0,5 m2
57.
Tip:
Het grondzeil is een rechthoek.
a.Het grondzeil is een rechthoek.
Oppervlakte grondzeil = lengte x breedte = 2 x 1 = 2 m2
b.
opp(voorkant / driehoek) = 1/2 x basis x hoogte = 1/2 x 1 x 1,2 = 0,6 m2
opp(achterkant / driehoek) = 1/2 x basis x hoogte = 1/2 x 1 x 1,2 = 0,6 m2
opp(rechthoek voor) = lengte x breedte = 2 x 1,3 = 2,6 m2
opp(rechthoek achter) = lengte x breedte = 2 x 1,3 = 2,6 m2
opp(grondzeil) = 2 m2
Totale oppervlakte van de hele tent: 8,4 m2
58.
Tip:
De vliegers zijn symmetrisch. Dus bereken steeds de oppervlakte van 1 kant. En dan maal 2.
a.De vliegers zijn symmetrisch. Dus bereken steeds de oppervlakte van 1 kant. En dan maal 2.
oppervlakte driehoek links 1 = 1/2 x basis x hoogte = 1/2 x 30 x 80 = 1200 cm2
oppervlakte driehoek links 2 = 1/2 x basis x hoogte = 1/2 x 110 x 25 = 1375 cm2
2 x (1200 + 1375) = 5150 cm2
b. 4000 cm2
Andere paragrafen:
2.1. Afstanden (1 t/m 10)
2.2. Middelloodlijn en omgeschreven cirkel (11 t/m 22)
2.3. Bissectrice en ingeschreven cirkel (23 t/m 33)
2.4. Zwaartelijn en hoogtelijn (34 t/m 44)
2.5. De oppervlakte van een driehoek (45 t/m 58)
2.6. De oppervlakte van een vierhoek (59 t/m 73)
2.1. Afstanden (1 t/m 10)
2.2. Middelloodlijn en omgeschreven cirkel (11 t/m 22)
2.3. Bissectrice en ingeschreven cirkel (23 t/m 33)
2.4. Zwaartelijn en hoogtelijn (34 t/m 44)
2.5. De oppervlakte van een driehoek (45 t/m 58)
2.6. De oppervlakte van een vierhoek (59 t/m 73)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


