Wiskunde.net

44.
a. x = -4
b. x = 11
c. x = 0
d. x = -8
e. x = 14
f. x = 0

45.
a. Ja, dat klopt.
b. Als je x = 3 invult in beide factoren dan wordt geen van de factoren 0.
c. Ja, vul in x = -3 levert: (-3 - 4)(-3 + 3) = -7 x 0 = 0.

46.
Dat 1 van de 2 getallen (factoren) gelijk moet zijn aan 0.

47.
a. x = -3 of x = 9
b. x = 0 of x = -5
c. x = 1 of x = -7 1/2
d. a = 0 of a = 20

48.
a. x + 3 = 0 v x - 3 = 0, levert x = -3 v x = 3
b. x = 0 v x + 3 = 0, levert x = 0 v x = -3
c. 2a - 5 = 0 v 2a - 5 = 0, levert a = 2½ v a = 2½
d. 5a = 0 v 2a + 7 = 0, levert a = 0 v a = -3½

49.
a. Van (x - 3)(x - 6) = 0 zijn 3 en 6 de oplossingen
b. Van (2x + 8)(3x - 27) = 0 zijn -4 en 9 de oplossingen
c. Van (x + 5)(½x - 4) = 0 zijn -5 en 8 de oplossingen
d. Van 5x(2x + 12) = 0 zijn 0 en -6 de oplossingen
e. Van (½x + 2)(5x - 12) = 0 zijn -4 en 2 2/5 de oplossingen

50.
a. x(x - 10) = 0 levert x = 0 v x = 10
b. x(3x + 2) = 0 levert x = 0 v x = -⅔

51.
a. (x + 1)(x + 2) = 0 dus x = -1 v x = -2
b. x(x - 12) = 0 dus x = 0 v x = 12
c. x(x + 50) = 0 dus x = 0 v x = -50
d. (x + 1)(x - 6) = 0 dus x = -1 v x = 6
e. (x + 1)(x - 2) = 0 dus x = -1 v x = 2
f. (x - 1)(x + 3) = 0 dus x = 2 v x = -3

52.
a. (x + 3)(x + 4) = 0 dus x = -3 v x = -4
b. (a + 3)(a - 4) = 0 dus a = -3 v a = 4
c. (a + 2)(a - 12) = 0 dus a = -2 v a = 12
d. (x - 4)(x - 6) = 0 dus x = 4 v x = 6
e. x(3x - 1) = 0 dus x = 0 v x = 1/3
f. 5x(x - 3) = 0 dus x = 0 v x = 3

53.
a. (y - 4)(y - 5) = 0 dus y = 4 v y = 5
b. (p - 5)(p + 7) = 0 dus p = 5 v p = -7
c. 3a(a + 4) = 0 dus a = 0 v a = -4
d. (x - 3)(x + 4) = 0 dus x = 3 v x = -4
e. t(5 - t) = 0 dus t = 0 v t = 5
f. (q + 7)(q + 9) = 0 dus q = -7 v q = -9

54.
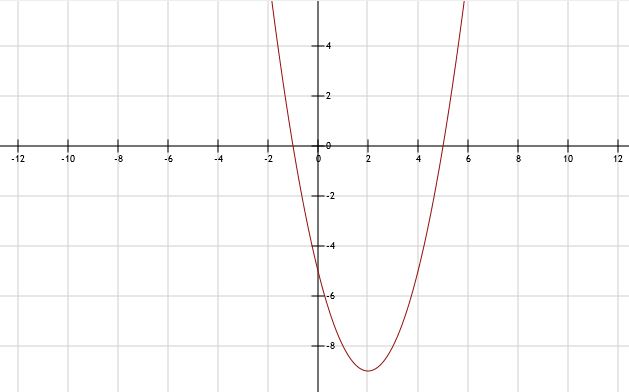
a. (x + 1)(x - 5) = 0 dus x = -1 v x = 5
b. Dus de snijpunten met de x-as zijn A(-1,0) en B(5,0).

55.
a. Snijpunten met de x-as: A(1,0) en B(3,0)
b. Snijpunten met de x-as: C(0,0) en D(6,0)
c. Snijpunten met de x-as: E(-1,0) en F(6,0)