TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 7.6 Kwadratische vergelijkingen oplossen HAVO/VWO 2
Boek: Getal & Ruimte - Kwadratische vergelijkingen HAVO/VWO 2 (deel 2) opgaven 56 t/m 71, 2010Hoe los je een kwadratische vergelijking op?
1. Maak het rechterlid nul, dus: x2 + 3x + 2 = 0
2. Ontbind het linkerlid in factoren, dus: (x + 1)(x + 2) = 0
3. Pas toe A x B = 0 dan is A = 0 of B = 0, dus: x + 1 = 0 of x + 2 = 0
4. Bepaal de oplossingen, dus x = -1 of x = -2
5. Controleer je antwoord door x = -1 en daarna x = -2 in te vullen in de vergelijking
1. Maak het rechterlid nul, dus: x2 + 3x + 2 = 0
2. Ontbind het linkerlid in factoren, dus: (x + 1)(x + 2) = 0
3. Pas toe A x B = 0 dan is A = 0 of B = 0, dus: x + 1 = 0 of x + 2 = 0
4. Bepaal de oplossingen, dus x = -1 of x = -2
5. Controleer je antwoord door x = -1 en daarna x = -2 in te vullen in de vergelijking
56.
A = 3 en B = 4 kan ook. Zo ook voor 2 en 6. Dus als A x B = 12 is niet noodzakelijk dat A of B gelijk is aan 12.
57.
a. Los op: x2 + 3x = 10
x2 + 3x = 10, stap 1 maak rechterlid = 0 door links en rechts -10 te doen:
x2 + 3x - 10 = 0, ontbind nu in factoren via een T-tabel van -10:
(x - 2)(x + 5) = 0, pas nu toe A x B = 0, dan A = 0 of B = 0:
x - 2 = 0 v x + 5 = 0, bepaal nu de oplossingen:
x = 2 v x = -5
Snijpunten van de parabool met de x-as zijn dus: (2,0) en (-5,0)
b. Los op: x2 - x = 12
x2 - x = 12, stap 1 maak rechterlid = 0 door links en rechts -12 te doen:
x2 - x - 12 = 0, ontbind nu in factoren via een T-tabel van -12:
(x + 3)(x - 4) = 0, pas nu toe A x B = 0, dan A = 0 of B = 0:
x + 3 = 0 v x - 4 = 0, bepaal nu de oplossingen:
x = -3 v x = 4
Snijpunten van de parabool met de x-as zijn dus: (-3,0) en (4,0)
c. Los op: x2 = 5x
x2 = 5x, stap 1 maak rechterlid = 0 door links en rechts -5x te doen:
x2 - 5x = 0, ontbind nu in factoren door x voor de haakjes te halen:
x(x - 5) = 0, pas nu toe A x B = 0, dan A = 0 of B = 0:
x = 0 v x - 5 = 0, bepaal nu de oplossingen:
x = 0 v x = 5
Snijpunten van de parabool met de x-as zijn dus: (0,0) en (5,0)
d. Los op: x2 - 5 = 4x
x2 - 5 = 4x, stap 1 maak rechterlid = 0 door links en rechts -4x te doen:
x2 - 4x - 5 = 0, ontbind nu in factoren via een T-tabel van -5:
(x + 1)(x - 5) = 0, pas nu toe A x B = 0, dan A = 0 of B = 0:
x + 1 = 0 v x - 5 = 0, bepaal nu de oplossingen:
x = -1 v x = 5
Snijpunten van de parabool met de x-as zijn dus: (-1,0) en (5,0)
e. Los op: x2 + 18 = 19x
x2 + 18 = 19x, stap 1 maak rechterlid = 0 door links en rechts -19x te doen:
x2 - 19x + 18 = 0, ontbind nu in factoren via een T-tabel van 18:
(x - 1)(x - 18) = 0, pas nu toe A x B = 0, dan A = 0 of B = 0:
x - 1 = 0 v x - 18 = 0, bepaal nu de oplossingen:
x = 1 v x = 18
Snijpunten van de parabool met de x-as zijn dus: (1,0) en (18,0)
f. Los op: x2 - 3x = 18
x2 - 3x = 18, stap 1 maak rechterlid = 0 door links en rechts -18 te doen:
x2 - 3x - 18 = 0, ontbind nu in factoren via een T-tabel van -18:
(x + 3)(x - 6) = 0, pas nu toe A x B = 0, dan A = 0 of B = 0:
x + 3 = 0 v x - 6 = 0, bepaal nu de oplossingen:
x = -3 v x = 6
Snijpunten van de parabool met de x-as zijn dus: (-3,0) en (6,0)
58.
a. (x - 1)(x + 4) = 0 dus x = 1 v x = -4
b. (x - 1)(x - 2) = 0 dus x = 1 v x = 2
c. x(x - 8) = 0 dus x = 0 v x = 8
d. (x + 2)(x - 3) = 0 dus x = -2 v x = 3
e. x(x + 10) = 0 dus x = 0 v x = -10
f. (x - 7)(x - 3) = 0 dus x = 7 v x = 3
59.
a. x(x - 2) = 0 dus x = 0 v x = 2
b. (x - 1)(x - 8) = 0 dus x = 1 v x = 8
c. 3x(x - 1) = 0 dus x = 0 v x = 1
d. (x + 1)(x - 2) = 0 dus x = -1 v x = 2
e. x(x + 5) = 0 dus x = 0 v x = -5
f. (x - 4)(x + 7) = 0 dus x = 4 v x = -7
60.
a. (x + 2)(x - 9) = 0 dus x = -2 v x = 9
b. x(x - 9) = 0 dus x = 0 v x = 9
c. x(x - 7) = 0 dus x = 0 v x = 7
d. (x - 7)(2x - 1) = 0 dus x = 7 v x = ½
e. (x + 1)(x - 8) = 0 dus x = -1 v x = 8
f. (x + 3)(x - 10) = 0 dus x = -3 v x = 10
61.
a. Oppervlakte ( II ) = lengte ⋅ breedte = 10x
Oppervlakte ( III ) = lengte ⋅ breedte = x ⋅ x = x2
b. Oppervlakte tegelpad = opp 1 + 2 + 3 = 5x + 10x + x2 = x2 + 15x
c. Los op: x2 + 15x = 34 leidt tot: (x - 2)(x + 17) = 0 dus x = 2 v x = -17
d. Tegelpad is dus 2 meter breed
62.
a. Oppervlakte ( I ) = lengte ⋅ breedte = 6x
Oppervlakte ( II ) = lengte ⋅ breedte = 8 ⋅ x = 8x
Oppervlakte ( III ) = lengte ⋅ breedte = x ⋅ x = x2
Oppervlakte tegelpad = opp 1 + 2 + 3 = 6x + 8x + x2 = x2 + 14x
b. x2 + 14x = 32
c. Los op: x2 + 14x = 32 leidt tot: (x - 2)(x + 16) = 0 dus x = 2 v x = -16
Tegelpad is dus 2 meter breed
63.
a. x(x + 9) = 0 dus x = 0 v x = -9
b. x = 3 v x = -3
c. Geen oplossingen, een kwadraat is nooit negatief
d. (x - 1)(x + 10) = 0 dus x = 1 v x = -10
e. 2x(x - 25) = 0 dus x = 0 v x = 25
f. x = 5 v x = -5
g. Geen oplossingen, een kwadraat is nooit negatief
h. (x - 6)(x + 8) = 0 dus x = 6 v x = -8
i. (x - 10)(x - 40) = 0 dus x = 10 v x = 40
64.
a. (x - 1)(x - 8) = 0 dus x = 1 v x = 8
b. x(x + 6) = 0 dus x = 0 v x = -6
c. x = 1 v x = -1
d. (x - 1)(x + 7) = 0 dus x = 1 v x = -7
e. (x - 3)(x + 11) = 0 dus x = 3 v x = -11
f. x2 = 4 dus x = 2 v x = -2
g. (x - 2)(x - 2) = 0 dus x = 2
h. x2 = 0 dus x = 0
i. (x - 2)(x - 5) = 0 dus x = 2 v x = 5
65.
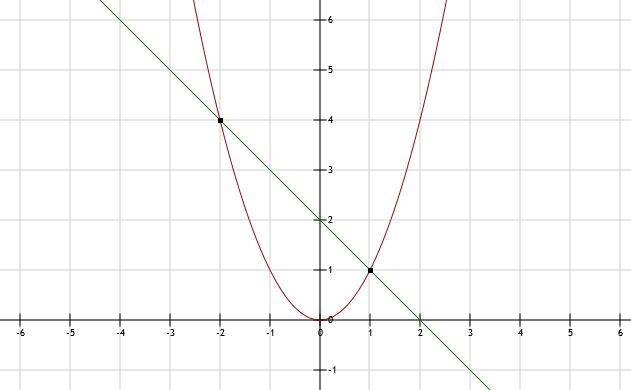
a. Parabool y = x2 (rood) en lijn y = -x + 2 (groen). Snijpunten: los op x2 = -x + 2
b. x2 + x - 2 = 0
(x - 1)(x + 2) = 0 dus x = 1 v x = -2
c. Bij x = -2 hoort y-waarde 4. Dus snijpunt A(-2,4).
Bij x = 1 hoort y-waarde 1. Dus snijpunt B(1,1).
A = 3 en B = 4 kan ook. Zo ook voor 2 en 6. Dus als A x B = 12 is niet noodzakelijk dat A of B gelijk is aan 12.
57.
a. Los op: x2 + 3x = 10
x2 + 3x = 10, stap 1 maak rechterlid = 0 door links en rechts -10 te doen:
x2 + 3x - 10 = 0, ontbind nu in factoren via een T-tabel van -10:
(x - 2)(x + 5) = 0, pas nu toe A x B = 0, dan A = 0 of B = 0:
x - 2 = 0 v x + 5 = 0, bepaal nu de oplossingen:
x = 2 v x = -5
Snijpunten van de parabool met de x-as zijn dus: (2,0) en (-5,0)
b. Los op: x2 - x = 12
x2 - x = 12, stap 1 maak rechterlid = 0 door links en rechts -12 te doen:
x2 - x - 12 = 0, ontbind nu in factoren via een T-tabel van -12:
(x + 3)(x - 4) = 0, pas nu toe A x B = 0, dan A = 0 of B = 0:
x + 3 = 0 v x - 4 = 0, bepaal nu de oplossingen:
x = -3 v x = 4
Snijpunten van de parabool met de x-as zijn dus: (-3,0) en (4,0)
c. Los op: x2 = 5x
x2 = 5x, stap 1 maak rechterlid = 0 door links en rechts -5x te doen:
x2 - 5x = 0, ontbind nu in factoren door x voor de haakjes te halen:
x(x - 5) = 0, pas nu toe A x B = 0, dan A = 0 of B = 0:
x = 0 v x - 5 = 0, bepaal nu de oplossingen:
x = 0 v x = 5
Snijpunten van de parabool met de x-as zijn dus: (0,0) en (5,0)
d. Los op: x2 - 5 = 4x
x2 - 5 = 4x, stap 1 maak rechterlid = 0 door links en rechts -4x te doen:
x2 - 4x - 5 = 0, ontbind nu in factoren via een T-tabel van -5:
(x + 1)(x - 5) = 0, pas nu toe A x B = 0, dan A = 0 of B = 0:
x + 1 = 0 v x - 5 = 0, bepaal nu de oplossingen:
x = -1 v x = 5
Snijpunten van de parabool met de x-as zijn dus: (-1,0) en (5,0)
e. Los op: x2 + 18 = 19x
x2 + 18 = 19x, stap 1 maak rechterlid = 0 door links en rechts -19x te doen:
x2 - 19x + 18 = 0, ontbind nu in factoren via een T-tabel van 18:
(x - 1)(x - 18) = 0, pas nu toe A x B = 0, dan A = 0 of B = 0:
x - 1 = 0 v x - 18 = 0, bepaal nu de oplossingen:
x = 1 v x = 18
Snijpunten van de parabool met de x-as zijn dus: (1,0) en (18,0)
f. Los op: x2 - 3x = 18
x2 - 3x = 18, stap 1 maak rechterlid = 0 door links en rechts -18 te doen:
x2 - 3x - 18 = 0, ontbind nu in factoren via een T-tabel van -18:
(x + 3)(x - 6) = 0, pas nu toe A x B = 0, dan A = 0 of B = 0:
x + 3 = 0 v x - 6 = 0, bepaal nu de oplossingen:
x = -3 v x = 6
Snijpunten van de parabool met de x-as zijn dus: (-3,0) en (6,0)
58.
a. (x - 1)(x + 4) = 0 dus x = 1 v x = -4
b. (x - 1)(x - 2) = 0 dus x = 1 v x = 2
c. x(x - 8) = 0 dus x = 0 v x = 8
d. (x + 2)(x - 3) = 0 dus x = -2 v x = 3
e. x(x + 10) = 0 dus x = 0 v x = -10
f. (x - 7)(x - 3) = 0 dus x = 7 v x = 3
59.
a. x(x - 2) = 0 dus x = 0 v x = 2
b. (x - 1)(x - 8) = 0 dus x = 1 v x = 8
c. 3x(x - 1) = 0 dus x = 0 v x = 1
d. (x + 1)(x - 2) = 0 dus x = -1 v x = 2
e. x(x + 5) = 0 dus x = 0 v x = -5
f. (x - 4)(x + 7) = 0 dus x = 4 v x = -7
60.
a. (x + 2)(x - 9) = 0 dus x = -2 v x = 9
b. x(x - 9) = 0 dus x = 0 v x = 9
c. x(x - 7) = 0 dus x = 0 v x = 7
d. (x - 7)(2x - 1) = 0 dus x = 7 v x = ½
e. (x + 1)(x - 8) = 0 dus x = -1 v x = 8
f. (x + 3)(x - 10) = 0 dus x = -3 v x = 10
61.
a. Oppervlakte ( II ) = lengte ⋅ breedte = 10x
Oppervlakte ( III ) = lengte ⋅ breedte = x ⋅ x = x2
b. Oppervlakte tegelpad = opp 1 + 2 + 3 = 5x + 10x + x2 = x2 + 15x
c. Los op: x2 + 15x = 34 leidt tot: (x - 2)(x + 17) = 0 dus x = 2 v x = -17
d. Tegelpad is dus 2 meter breed
62.
a. Oppervlakte ( I ) = lengte ⋅ breedte = 6x
Oppervlakte ( II ) = lengte ⋅ breedte = 8 ⋅ x = 8x
Oppervlakte ( III ) = lengte ⋅ breedte = x ⋅ x = x2
Oppervlakte tegelpad = opp 1 + 2 + 3 = 6x + 8x + x2 = x2 + 14x
b. x2 + 14x = 32
c. Los op: x2 + 14x = 32 leidt tot: (x - 2)(x + 16) = 0 dus x = 2 v x = -16
Tegelpad is dus 2 meter breed
63.
a. x(x + 9) = 0 dus x = 0 v x = -9
b. x = 3 v x = -3
c. Geen oplossingen, een kwadraat is nooit negatief
d. (x - 1)(x + 10) = 0 dus x = 1 v x = -10
e. 2x(x - 25) = 0 dus x = 0 v x = 25
f. x = 5 v x = -5
g. Geen oplossingen, een kwadraat is nooit negatief
h. (x - 6)(x + 8) = 0 dus x = 6 v x = -8
i. (x - 10)(x - 40) = 0 dus x = 10 v x = 40
64.
a. (x - 1)(x - 8) = 0 dus x = 1 v x = 8
b. x(x + 6) = 0 dus x = 0 v x = -6
c. x = 1 v x = -1
d. (x - 1)(x + 7) = 0 dus x = 1 v x = -7
e. (x - 3)(x + 11) = 0 dus x = 3 v x = -11
f. x2 = 4 dus x = 2 v x = -2
g. (x - 2)(x - 2) = 0 dus x = 2
h. x2 = 0 dus x = 0
i. (x - 2)(x - 5) = 0 dus x = 2 v x = 5
65.
a. Parabool y = x2 (rood) en lijn y = -x + 2 (groen). Snijpunten: los op x2 = -x + 2
b. x2 + x - 2 = 0
(x - 1)(x + 2) = 0 dus x = 1 v x = -2
c. Bij x = -2 hoort y-waarde 4. Dus snijpunt A(-2,4).
Bij x = 1 hoort y-waarde 1. Dus snijpunt B(1,1).

66.
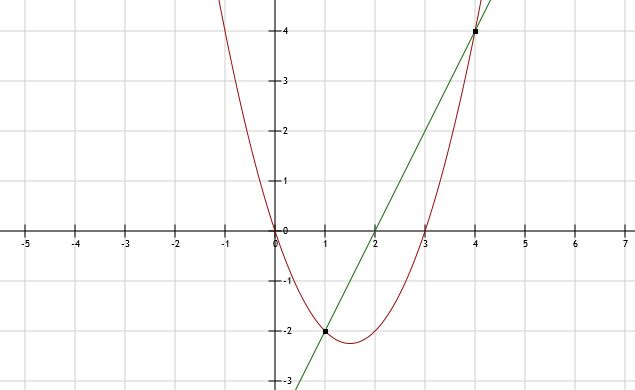
a. Parabool y = x2 - 3x (rood) en lijn y = 2x - 4 (groen). Snijpunten: los op x2 - 3x = 2x - 4
x2 - 5x + 4 = 0
(x - 1)(x - 4) = 0 dus x = 1 v x = 4
Bij x = 1 hoort y-waarde -2. Dus snijpunt A(1,-2).
Bij x = 4 hoort y-waarde 4. Dus snijpunt B(4,4).
67.
a. x = -1 v x = 7
b. Die is al ontbonden in de juiste factoren. Je kunt meteen a x b = 0 toepassen (a = 0 v b = 0).
68.
Werk eerst de haakjes weg en herleid dan het linkerlid. Maak dan het rechterlid nul. Je krijgt dan:
a. (x - 2)(x + 8) = 0 dus x = 2 v x = -8
b. x(x + 1) = 0 dus x = 0 v x = -1
c. (x + 3)(x - 8) = 0 dus x = -3 v x = 8
d. x(x + 6) = 0 dus x = 0 v x = -6
e. (x + 3)(x - 5) = 0 dus x = -3 v x = 5
f. (2x + 1)(x - 1) = 0 dus x = -1/2 v x = 1
69.
a. x = -1 v x = 4
b. x = 5 v x = -7
c. x = 1 v x = 9
d. x = -2 v x = 7
e. x = -3 v x = 2
f. x = 1 v x = 7
70.
a. x(x + 2) = 24
b. x(x + 2) = 24
x2 + 2x = 24
x2 + 2x - 24 = 0
(x - 4)(x + 6) = 0
x - 4 = 0 v x + 6 = 0
x = 4 v x = -6
c. Breedte terras dus 4 meter en lengte 6 meter.
71.
a. x(x + 5) = 126
b. x(x + 5) = 126
x2 + 5x = 126
x2 + 5x - 126 = 0
(x - 9)(x + 14) = 0
x - 9 = 0 v x + 14 = 0
x = 9 v x = -14
c. Breedte bassin dus 9 meter en lengte 9 + 5 = 14 meter.
a. Parabool y = x2 - 3x (rood) en lijn y = 2x - 4 (groen). Snijpunten: los op x2 - 3x = 2x - 4
x2 - 5x + 4 = 0
(x - 1)(x - 4) = 0 dus x = 1 v x = 4
Bij x = 1 hoort y-waarde -2. Dus snijpunt A(1,-2).
Bij x = 4 hoort y-waarde 4. Dus snijpunt B(4,4).

67.
a. x = -1 v x = 7
b. Die is al ontbonden in de juiste factoren. Je kunt meteen a x b = 0 toepassen (a = 0 v b = 0).
68.
Werk eerst de haakjes weg en herleid dan het linkerlid. Maak dan het rechterlid nul. Je krijgt dan:
a. (x - 2)(x + 8) = 0 dus x = 2 v x = -8
b. x(x + 1) = 0 dus x = 0 v x = -1
c. (x + 3)(x - 8) = 0 dus x = -3 v x = 8
d. x(x + 6) = 0 dus x = 0 v x = -6
e. (x + 3)(x - 5) = 0 dus x = -3 v x = 5
f. (2x + 1)(x - 1) = 0 dus x = -1/2 v x = 1
69.
a. x = -1 v x = 4
b. x = 5 v x = -7
c. x = 1 v x = 9
d. x = -2 v x = 7
e. x = -3 v x = 2
f. x = 1 v x = 7
70.
a. x(x + 2) = 24
b. x(x + 2) = 24
x2 + 2x = 24
x2 + 2x - 24 = 0
(x - 4)(x + 6) = 0
x - 4 = 0 v x + 6 = 0
x = 4 v x = -6
c. Breedte terras dus 4 meter en lengte 6 meter.
71.
a. x(x + 5) = 126
b. x(x + 5) = 126
x2 + 5x = 126
x2 + 5x - 126 = 0
(x - 9)(x + 14) = 0
x - 9 = 0 v x + 14 = 0
x = 9 v x = -14
c. Breedte bassin dus 9 meter en lengte 9 + 5 = 14 meter.
Andere paragrafen:
7.1. Grafieken en vergelijkingen (1 t/m 9)
7.2. Vergelijkingen van de vorm x2 = c (10 t/m 19)
7.3. Buiten haakjes halen (20 t/m 29)
7.4. De product-som-methode (30 t/m 43)
7.5. Kwadratische vergelijkingen (44 t/m 55)
7.6. Kwadratische vergelijkingen oplossen (56 t/m 71)
7.1. Grafieken en vergelijkingen (1 t/m 9)
7.2. Vergelijkingen van de vorm x2 = c (10 t/m 19)
7.3. Buiten haakjes halen (20 t/m 29)
7.4. De product-som-methode (30 t/m 43)
7.5. Kwadratische vergelijkingen (44 t/m 55)
7.6. Kwadratische vergelijkingen oplossen (56 t/m 71)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


