Lijn door 2 gegeven punten
Bron: Wiskunde.net - onderwerpen, 04-02-2026Video
Hoe bepalen we een lijn door 2 gegeven punten? De video legt uit hoe je de 'a' en 'b' berekent.
Inleiding
Hoe bepalen we een lijn l: door 2 gegeven punten die te vinden zijn in een assenstelsel? Begin eerst met de basisformule: y = ax + b, waarbij
y de waarde vertegenwoordigt op de verticale as en de x de waarde vertegenwoordigt op de horizontale as.
Zo kun je dus ook beginnen als basisvergelijking K = at + b, met K als de verticale as en t als de horizontale as.
We noemen 'a' ook wel de richtingscoëfficiënt van de lijn (schrijf: rcl). En 'b' is het snijpunt met de y-as (verticale as).
De 'a' is de verhouding verticale verplaatsing / horizontale verplaatsing: rcl = Δy / Δx.
We bepalen hier dus het verschil tussen de y-coördinaten en de x-coördinaten van de 2 punten. Deze delen we op elkaar.
De rcl houdt in hoeveel je omhoog moet wanneer je 1 hokje naar rechts gaat. Je kunt dan dus het bekende trapje tekenen 'tegen' de lijn.
Je tekent dan: '1 naar rechts' en dan 'a omhoog'.
Een negatieve 'omhoog' betekent dus omlaag. Bijvoorbeeld: rcl = -3. Dit betekent: '1 naar rechts' en '-3 omhoog'. Ofwel: '1 naar rechts' en '3 omlaag'. De lijn heeft dan dus een dalende helling.
Als:
- 'a' groter dan 0 (a>0): dan is de lijn stijgend.
- 'a' kleiner dan 0 (a<0): dan is de lijn dalend.
- 'a' gelijk is aan 0 (a=0): dan is de lijn horizontaal.
Op Wiskunde.net kun je zelf online lijnen tekenen.
Formule Lijn door 2 gegeven punten
Voorbeeld Lijn door 2 gegeven punten
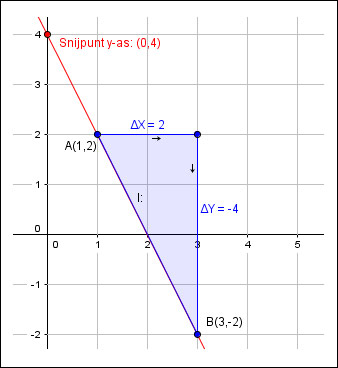
Stel de formule van de lijn l: op door de punten: A(1,2) en B(3,-2)
Uitwerking:
Teken zelf de punten A en B in een assenstelsel en trek de lijn l: door deze punten.
Maak tevens een driehoek.
Neem als basisvergelijking: y = ax + b en bereken de 'a' en 'b'.
a = Δy / Δx = (YB - YA) / (XB - XA) = (-2 - 2) / (3 - 1) = -4 / 2 = -2
Snijpunt met de y-as: (0,4) dus b = 4
Dus de vergelijking van de lijn l: wordt: y = -2x + 4.
Ter controle: Vul A(1,2) en B(3,-2) in y = -2x + 4 en zie dat het klopt. Dat wil zeggen dat er een 'ware' bewering staat.
Extra
De richtingscoëfficiënt is hetzelfde als de helling, ofwel de 'a'.
Voor meer uitleg en opgaven over 'een lijn door 2 punten', klik dan hier...
Gerelateerd
Tangens van een hoek Een rechthoekige driehoek bestaat uit 2 rechthoekszijden. Een rec...
Cosinusregel In deze video leggen we uit aan de hand van een voorbeeld hoe de ...
Sinusregel In deze video leggen we uit aan de hand van een voorbeeld hoe de ...