TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 1.3 Exponentiële verbanden VMBO 4 KGT
Boek: Getal & Ruimte - Verbanden 1 VMBO 4 (deel 1) opgaven 30 t/m 40, 2011Wat zijn exponentiële verbanden?
De basisformule van een exponentieel verband is: aantal = begingetal x groeifactortijd.
Bijvoorbeeld: spaargeld = 425 x 1,05t. Hierbij is sprake van een exponentieel verband tussen de tijd t en het spaargeld in euro's.
Omdat er in de formule een exponent staat (t), spreken we van een exponentieel verband.
Nog enkele voorbeelden van exponentiële verbanden: aantal bacteriën = 3500 x 1,36t of aantal = 20 x 0,98t
Teken een grafiek om meer inzicht te krijgen tussen het verband en de twee variabelen.
De basisformule van een exponentieel verband is: aantal = begingetal x groeifactortijd.
Bijvoorbeeld: spaargeld = 425 x 1,05t. Hierbij is sprake van een exponentieel verband tussen de tijd t en het spaargeld in euro's.
Omdat er in de formule een exponent staat (t), spreken we van een exponentieel verband.
Nog enkele voorbeelden van exponentiële verbanden: aantal bacteriën = 3500 x 1,36t of aantal = 20 x 0,98t
Teken een grafiek om meer inzicht te krijgen tussen het verband en de twee variabelen.
30.
b. Als de tijd met 1 toeneemt, neemt het aantal met vaste eenheid van 20 toe.
c. (t + 1)*20 = 640, dus t = 31
31.
a.
b. Als de tijd met 1 toeneemt, neemt het aantal NIET met een vaste eenheid toe. De toename is niet constant, maar verandert steeds.
c. Zie tabel, na 5 dagen zijn er 640 zieke mensen.
32.
b. Groeifactor is 3.
c. Begingetal is 5.
d. De formule is: aantal = 5 x 3t
33.
b. De tabellen II en III.
c. Formule bij tabel II: aantal = 1500 x 1,5t
Formule bij tabel III: aantal = 20 x 3t
34.
a.
Tabel I:
Tabel II:
b. Formule bij tabel I: aantal = 100 x 40t
Formule bij tabel II: aantal = 2 x 10t
35.
a.
Tabel I:
Tabel II:
b. Formule bij tabel I: aantal = 75 x 1,2t
Formule bij tabel II: aantal x 1000 = 100 x 1,8t
36.
b. Na 2 jaar zijn er 1152 wolven.
c. Na 3 jaar zijn er 1382 wolven.
d. Stijging in jaar 3 is: 1382 - 1152 = 230 wolven
37.
t = 6 geeft aantal 20 x 46 = 81 920
Toename = 327 680 - 81 920 = 245 760 insecten
38.
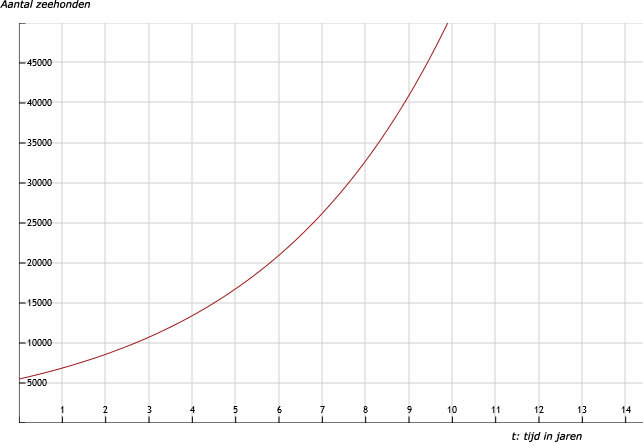
b. Bij 2018 hoort t = 9. Dit levert: aantal = 5500 x 1,259 = 40 978 zeehonden
c. Bij t = 8 hoort aantal: 32 783. Dan 40 978 - 32 783 = 8 195. Dus de toename is 8 195 in 2018.
d. Zie afbeelding
39.
a. Bij 2013 hoort t = 4 en dat levert: aantal = 2,06 x 1,084 ≈ 2,80 miljard pinbetalingen.
b. Bij 2018 hoort t = 9 en dat levert: aantal = 2,06 x 1,089 ≈ 4,12 miljard pinbetalingen.
c. Bij t = 12 gaan we eerst door de 5 miljard. Dat is dus in 2021.
Tip:
Bij een lineair verband neemt bij een constante stijging in de tijd (bijvoorbeeld t steeds +1) het aantal ook met een vaste waarde toe.
a.
Bij een lineair verband neemt bij een constante stijging in de tijd (bijvoorbeeld t steeds +1) het aantal ook met een vaste waarde toe.
| tijd in dagen | 0 | 1 | 2 | 3 | 4 | 5 |
| aantal | 20 | 40 | 60 | 80 | 100 | 120 |
b. Als de tijd met 1 toeneemt, neemt het aantal met vaste eenheid van 20 toe.
c. (t + 1)*20 = 640, dus t = 31
31.
a.
| tijd in dagen | 0 | 1 | 2 | 3 | 4 | 5 |
| aantal | 20 | 40 | 80 | 160 | 320 | 640 |
b. Als de tijd met 1 toeneemt, neemt het aantal NIET met een vaste eenheid toe. De toename is niet constant, maar verandert steeds.
c. Zie tabel, na 5 dagen zijn er 640 zieke mensen.
32.
Tip:
Bij tabel 1: als t steeds met 1 toeneemt, neemt het aantal steeds toe met de vaste waarde 10. Dus een lineair verband.
a. Bij tabel 2.Bij tabel 1: als t steeds met 1 toeneemt, neemt het aantal steeds toe met de vaste waarde 10. Dus een lineair verband.
b. Groeifactor is 3.
c. Begingetal is 5.
d. De formule is: aantal = 5 x 3t
33.
Tip:
Formule: aantal = begingetal x groeifactortijd
a. 130/100 = 1,3 en 190/160 = 1,9 en 220/190 = 1,16, dus de groei is niet steeds hetzelfde.Formule: aantal = begingetal x groeifactortijd
b. De tabellen II en III.
c. Formule bij tabel II: aantal = 1500 x 1,5t
Formule bij tabel III: aantal = 20 x 3t
34.
a.
Tabel I:
| t | 0 | 1 | 2 | 3 | 4 | 5 | |
| aantal | 100 | 4000 | 160 000 | 6 400 000 | 256 000 000 | 10 240 000 000 | steeds x40, dus groeifactor is 40 |
Tabel II:
| t | 0 | 1 | 2 | 3 | 4 | 5 | |
| aantal | 2 | 20 | 200 | 2000 | 20 000 | 200 000 | steeds x10, dus groeifactor is 10 |
b. Formule bij tabel I: aantal = 100 x 40t
Formule bij tabel II: aantal = 2 x 10t
35.
a.
Tabel I:
| t | 0 | 1 | 2 | 3 | 4 | 5 | |
| aantal | 75 | 90 | 108 | 129,6 | 155,52 | 186,624 | steeds x1,2, dus groeifactor is 1,2 |
Tabel II:
| t | 0 | 1 | 2 | 3 | 4 | 5 | |
| aantal | 100 | 180 | 324 | 583,2 | 1049,76 | 1889,568 | steeds x1,8, dus groeifactor is 1,8 |
b. Formule bij tabel I: aantal = 75 x 1,2t
Formule bij tabel II: aantal x 1000 = 100 x 1,8t
36.
Tip:
Rond af op hele decimalen. We hebben niets aan 1382,4 wolven.
a. Rond af op hele decimalen. We hebben niets aan 1382,4 wolven.
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| aantal wolven | 800 | 960 | 1152 | 1382 | 1659 | 1991 | 2389 |
b. Na 2 jaar zijn er 1152 wolven.
c. Na 3 jaar zijn er 1382 wolven.
d. Stijging in jaar 3 is: 1382 - 1152 = 230 wolven
37.
Tip:
Toename in de zevende week = aantal week 7 - aantal week 6
t = 7 geeft aantal 20 x 47 = 327 680Toename in de zevende week = aantal week 7 - aantal week 6
t = 6 geeft aantal 20 x 46 = 81 920
Toename = 327 680 - 81 920 = 245 760 insecten
38.
Tip:
Bij t = 0 hoort 2009, bij t = 1 hoort 2010, bij t = 2 hoort 2011, bij t = 3 hoort 2012 enz.
a. aantal = 5500 x 1,25tBij t = 0 hoort 2009, bij t = 1 hoort 2010, bij t = 2 hoort 2011, bij t = 3 hoort 2012 enz.
b. Bij 2018 hoort t = 9. Dit levert: aantal = 5500 x 1,259 = 40 978 zeehonden
c. Bij t = 8 hoort aantal: 32 783. Dan 40 978 - 32 783 = 8 195. Dus de toename is 8 195 in 2018.
d. Zie afbeelding
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| aantal zeehonden | 5500 | 6875 | 8594 | 10 742 | 13 428 | 16 785 | 20 981 | 26 226 | 32 783 | 40 978 | 51 223 |

39.
a. Bij 2013 hoort t = 4 en dat levert: aantal = 2,06 x 1,084 ≈ 2,80 miljard pinbetalingen.
b. Bij 2018 hoort t = 9 en dat levert: aantal = 2,06 x 1,089 ≈ 4,12 miljard pinbetalingen.
c. Bij t = 12 gaan we eerst door de 5 miljard. Dat is dus in 2021.
40.
b. Hoogte bal bij n = 3 levert h = 0,432 meter
c. Hoogte bal bij n = 5 levert h = 0,16 meter
d. De hoogte wordt steeds met 0,6 vermenigvuldigd.
e.
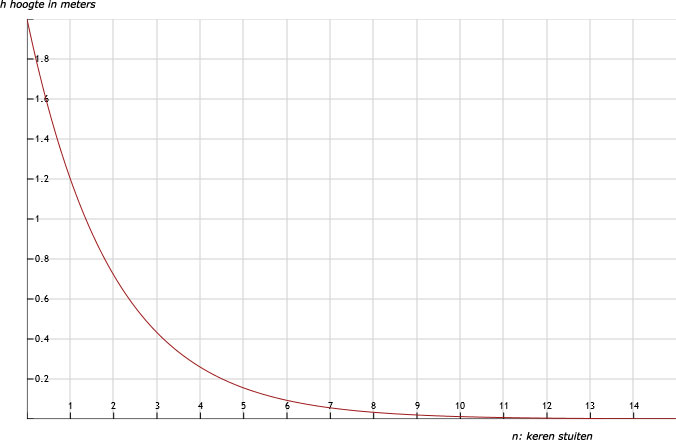
f. Zie afbeelding
g. De hoogte daalt. Dus neemt af. Het klinkt dan raar om van een groei te spreken.
Tip:
0,60 = 1
a. Kies n = 0 en dat levert 2. Dus de hoogte is 2.0,60 = 1
b. Hoogte bal bij n = 3 levert h = 0,432 meter
c. Hoogte bal bij n = 5 levert h = 0,16 meter
d. De hoogte wordt steeds met 0,6 vermenigvuldigd.
e.
| n stuiten | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| h hoogte in meters | 2 | 1,2 | 0,72 | 0,432 | 0,259 | 0,156 | 0,09 | 0,06 | 0,03 | 0,02 | 0,01 |
f. Zie afbeelding
g. De hoogte daalt. Dus neemt af. Het klinkt dan raar om van een groei te spreken.

Andere paragrafen:
1.1. Machtsverbanden (1 t/m 15)
1.2. Wortelverbanden (16 t/m 29)
1.3. Exponentiële verbanden (30 t/m 40)
1.4. Exponentiele groei en procenten (41 t/m 62)
1.5. Gemengde opgaven (63 t/m 73)
1.1. Machtsverbanden (1 t/m 15)
1.2. Wortelverbanden (16 t/m 29)
1.3. Exponentiële verbanden (30 t/m 40)
1.4. Exponentiele groei en procenten (41 t/m 62)
1.5. Gemengde opgaven (63 t/m 73)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


