TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 1.4 Exponentiele groei en procenten VMBO 4 KGT
Boek: Getal & Ruimte - Verbanden 1 VMBO 4 (deel 1) opgaven 41 t/m 62, 2011Van percentage naar groeifactor
Bij een toename van 5,5% krijg je 100% + 5,5% = 105,5%. De groeifactor die we dan krijgen is: 105,5 / 100 = 1,055.
Bij een afname van 5,5% krijg je 100% - 5,5% = 94,5%. De groeifactor die we dan krijgen is: 94,5 / 100 = 0,945.
Bij een toename van 5,5% krijg je 100% + 5,5% = 105,5%. De groeifactor die we dan krijgen is: 105,5 / 100 = 1,055.
Bij een afname van 5,5% krijg je 100% - 5,5% = 94,5%. De groeifactor die we dan krijgen is: 94,5 / 100 = 0,945.
41.
a. Bedrag dat op de bank wordt gezet is: 250 euro.
b. 1,035 x 100% = 103,5%. Dus de toename is 3,5%.
c. Na 2 jaar staat er op de bank: 250 x 1,0352 = 267,81 euro.
d. Na 3 jaar staat er op de bank: 250 x 1,0353 = 277,18 euro.
42.
b. Bij 2008 hoort t = 2. We krijgen dan aantal = 175 x 1,0122 = 179 leguanen
c. Bij 2020 hoort t = 14. We krijgen dan aantal = 175 x 1,01214 = 207 leguanen
d. Bij t = 59 gaan we voor het eerst door de 350 heen. Dat is dus in 2065.
Tip: laat de formule 175*1.012^4 in je rekenmachine staan en kies steeds een hogere waarde van t.
43.
44.
45.
b. Bij t = 5 is de hoogte: 425 x 0,955 = 328,9 cm
c. 0,95 x 100% = 95% en 95% - 100% = -5%
d. Bij t = 48 is de hoogte: 425 x 0,9548 = 36,2 cm
46.
b. Neem t = 2 levert: luchtdruk = 2,5 x 0,92 = 2,025 bar
47.
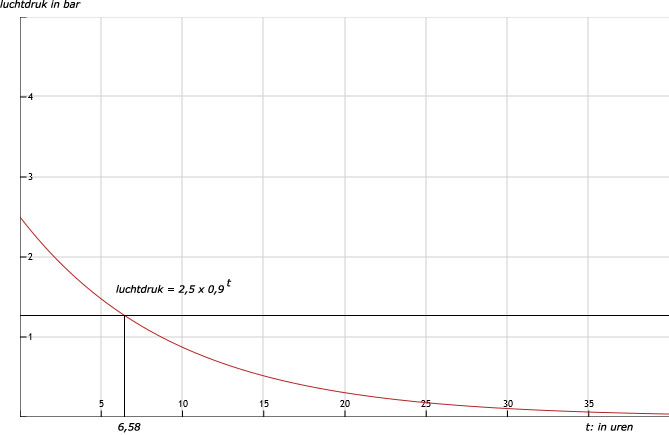
b. Bij t = 6 is de druk nog 1,33 en bij t = 7 is de druk 1,20. Met inklemmen kies t = 6,57 en t = 6,58. Bij t = 6,58 schiet de druk onder de 1,25.
c. 6,58 uur => 6 uur en 34 minuten en 48 sec.
48.
b. Bij t = 3 dan is de waarde: 1500 x 0,8253 = 842,27 euro
c. Bij t = 3 is de waarde 842,27 euro (dus nog niet op de helft) en bij t = 4 is de waarde 694,88 euro. Dus wel gehalveerd. Dus na 4 jaar.
d. Bij t = 5 dan is de waarde: 1500 x 0,8255 = 573,27 euro. Dus de verkoopprijs is hoger dan de waarde. Dus een goede deal.
49.
50.
a. Bedrag dat op de bank wordt gezet is: 250 euro.
b. 1,035 x 100% = 103,5%. Dus de toename is 3,5%.
c. Na 2 jaar staat er op de bank: 250 x 1,0352 = 267,81 euro.
d. Na 3 jaar staat er op de bank: 250 x 1,0353 = 277,18 euro.
42.
Tip:
Bij een toename van 1,2% krijg je 100% + 1,2% = 101,2%. De groeifactor die we dan krijgen is: 101,2 / 100 = 1,012.
a. formule: aantal = 175 x 1,012tBij een toename van 1,2% krijg je 100% + 1,2% = 101,2%. De groeifactor die we dan krijgen is: 101,2 / 100 = 1,012.
b. Bij 2008 hoort t = 2. We krijgen dan aantal = 175 x 1,0122 = 179 leguanen
c. Bij 2020 hoort t = 14. We krijgen dan aantal = 175 x 1,01214 = 207 leguanen
d. Bij t = 59 gaan we voor het eerst door de 350 heen. Dat is dus in 2065.
Tip: laat de formule 175*1.012^4 in je rekenmachine staan en kies steeds een hogere waarde van t.
43.
| formule | begingetal | groeifactor | toename in % | hoeveelheid na 5 jaar |
| B = 300 x 1,15t | 300 | 1,15 | 15% | 603,41 |
| B = 300 x 1,08t | 300 | 1,08 | 8% | 440,80 |
| B = 80 x 1,12t | 80 | 1,12 | 12% | 140,99 |
| B = 1800 x 1,003t | 1800 | 1,003 | 0,3% | 1827,16 |
44.
| formule | begingetal | groeifactor | toename in % | hoeveelheid na 10 jaar |
| B = 600 x 1,07t | 600 | 1,07 | 7% | 1180,29 |
| B = 500 x 1,08t | 500 | 1,08 | 8% | 1079,46 |
| B = 250 x 2,5t | 250 | 2,5 | 150% | 2 384 185,79 |
| B = 1800 x 1,23t | 1800 | 1,23 | 23% | 14 266,70 |
45.
Tip:
2 dagen is gelijk aan 48 uur
a. Bij t = 0 is de hoogte: 425 x 0,950 = 425 cm2 dagen is gelijk aan 48 uur
b. Bij t = 5 is de hoogte: 425 x 0,955 = 328,9 cm
c. 0,95 x 100% = 95% en 95% - 100% = -5%
d. Bij t = 48 is de hoogte: 425 x 0,9548 = 36,2 cm
46.
Tip:
Formule: aantal = begingetal x groeifactortijd
a. formule van de luchtdruk in de band = 2,5 x 0,9tFormule: aantal = begingetal x groeifactortijd
b. Neem t = 2 levert: luchtdruk = 2,5 x 0,92 = 2,025 bar

47.
Tip:
3 kwartier = 0,75 uur
1 uur = 3600 sec
0,01 uur = 36 sec
0,58 uur = 2088 sec
En 2088 sec / 60 = 34,8 minuten en 0,8 minuten is 48 sec.
a. Neem t = 0,75 levert: luchtdruk = 2,5 x 0,90,75 = 2,31 bar3 kwartier = 0,75 uur
1 uur = 3600 sec
0,01 uur = 36 sec
0,58 uur = 2088 sec
En 2088 sec / 60 = 34,8 minuten en 0,8 minuten is 48 sec.
b. Bij t = 6 is de druk nog 1,33 en bij t = 7 is de druk 1,20. Met inklemmen kies t = 6,57 en t = 6,58. Bij t = 6,58 schiet de druk onder de 1,25.
c. 6,58 uur => 6 uur en 34 minuten en 48 sec.
48.
Tip:
groeifactor = (100% - 17,5%) / 100
a. Formule: 1500 x 0,825tgroeifactor = (100% - 17,5%) / 100
b. Bij t = 3 dan is de waarde: 1500 x 0,8253 = 842,27 euro
c. Bij t = 3 is de waarde 842,27 euro (dus nog niet op de helft) en bij t = 4 is de waarde 694,88 euro. Dus wel gehalveerd. Dus na 4 jaar.
d. Bij t = 5 dan is de waarde: 1500 x 0,8255 = 573,27 euro. Dus de verkoopprijs is hoger dan de waarde. Dus een goede deal.
49.
| begingetal in euro | afname in % | groeifactor | formule | hoeveelheid na 5 jaar |
| 300 | 15% | 0,85 | B = 300 x 0,85t | 133,11 euro |
| 300 | 35% | 0,65 | B = 300 x 0,65t | 34,81 euro |
| 200 | 13% | 0,87 | B = 200 x 0,87t | 99,68 euro |
50.
Tip:
groeifactor = (100% +/- %) / 100
groeifactor = (100% +/- %) / 100
| begingetal in euro | afname/toename in % | groeifactor | formule | hoeveelheid na 8 jaar |
| 200 | -1,3% | 0,987 | B = 200 x 0,987t | 180,12 euro |
| 500 | 25% | 1,25 | B = 500 x 1,25t | 2980,23 euro |
| 150 | 0,7% | 1,007 | B = 150 x 1,007t | 158,61 euro |
51.
b. Beginhoogte = 3 meter
c. Hoogte = begingetal x groeifactorn = 3 x 0,75n
d. hoogte bal = 3 x 0,753 = 1,27 meter
52.
b. Invullen t = 4 levert: 203 x 0,894 ≈ 127 mensen
c. Invullen t = 7 levert: 203 x 0,897 ≈ 90 mensen
d. Gebruik de formule om in te klemmen:
bij t = 11 levert 56 mensen
bij t = 12 levert 50 mensen
bij t = 13 levert 45 mensen
Dus op 1 januari 2020 staan we op 50 mensen. Dus in de loop van 2020 komen we onder de 50 werknemers.
53.
b. De oppervlakte is verdubbeld bij 24 m2.
Bij t = 3 is de oppervlakte kroos: 12 x 1,233 = 22,33 m2 (net te weinig)
Bij t = 4 is de oppervlakte kroos: 12 x 1,234 = 27,47 m2
Dus na 4 dagen.
c. Bij welke t is de oppervlakte gelijk aan 80?
Bij t = 9 is de oppervlakte kroos: 12 x 1,239 = 77,33 m2 (net te weinig)
Bij t = 10 is de oppervlakte kroos: 12 x 1,2310 = 95,11 m2
Dus na 10 dagen.
54.
Bij t = 7 is de oppervlakte kroos: 6 x 1,127 = 13,26 m2
Dus na 7 dagen is de oppervlakte kroos verdubbeld.
55.
b. Na hoeveel weken is het aantal vissen gelijk aan 25?
Bij t = 4 is het aantal vissen gedaald tot: 50 x 0,864 = 27,35 vissen (net te weinig)
Bij t = 5 is het aantal vissen gedaald tot: 50 x 0,865 = 23,52 vissen
Bij t = 4,5 is het aantal vissen gedaald tot: 50 x 0,864,5 = 25,36 vissen (we zijn er bijna!)
Bij t = 4,6 is het aantal vissen gedaald tot: 50 x 0,864,6 = 24,98 vissen (we zijn er!)
Dus na 4,6 weken is de hoeveelheid vissen gehalveerd.
56.
Bij een afname van 8,2% hoort een groeifactor: (100% - 8,2%) / 100 = 0,918
Formule wordt: 1200 x 0,918t, t in jaren
Wanneer is het aantal zeeleeuwen gelijk aan 600?
Bij t = 8 krijgen we: aantal = 1200 x 0,9188 ≈ 605
Bij t = 9 krijgen we: aantal = 1200 x 0,9189 ≈ 556
Bij t = 8,1 krijgen we: aantal = 1200 x 0,9188,1 ≈ 600,08 (bijna!)
Bij t = 8,2 krijgen we: aantal = 1200 x 0,9188,2 ≈ 594,96
Dus de halveringstijd is 8,2 jaren.
57.
a. groeifactor: (100% - 11%) / 100 = 0,89
b. Formule: 100 x 0,89t
Bij t = 5 krijgen we: aantal = 100 x 0,895 ≈ 55,84
Bij t = 6 krijgen we: aantal = 100 x 0,896 ≈ 49,70
Dus de halveringstijd is 6 maanden.
58.
a. Nee, want na 3200 jaar is er nog de helft van de helft (is 1/4) over.
b. Na 1600 jaar is de hoeveelheid gehalveerd. Dus is er nog 4 kg over.
c. Na nog eens 1600 jaar is die 4 kg weer gehalveerd. Je houdt dus 2 kg over.
d. Kies: aantal kg = 8 x 0,999561600 ≈ 4. Als je formule I en II tot de macht 1600 neemt, dan gaat het naar 0. Dus geen halvering na 1600 jaar. Sterker nog: formule I heeft een halvering na 1 jaar!
59.
60.
Bij t = 11 krijgen we: aantal = 600 x 1,02511 ≈ 787,25 euro
Bij t = 12 krijgen we: aantal = 600 x 1,02512 ≈ 806,93 euro
Dus na 12 jaren.
Tip:
Formule: aantal = begingetal x groeifactorn
a. groeifactor = (100% - 25%) / 100 = 0,75Formule: aantal = begingetal x groeifactorn
b. Beginhoogte = 3 meter
c. Hoogte = begingetal x groeifactorn = 3 x 0,75n
d. hoogte bal = 3 x 0,753 = 1,27 meter
52.
Tip:
t = 0 hoort bij 2008 dan hoort t = 4 bij 2012
a. Formule aantal werknemers: 203 x 0,89tt = 0 hoort bij 2008 dan hoort t = 4 bij 2012
b. Invullen t = 4 levert: 203 x 0,894 ≈ 127 mensen
c. Invullen t = 7 levert: 203 x 0,897 ≈ 90 mensen
d. Gebruik de formule om in te klemmen:
bij t = 11 levert 56 mensen
bij t = 12 levert 50 mensen
bij t = 13 levert 45 mensen
Dus op 1 januari 2020 staan we op 50 mensen. Dus in de loop van 2020 komen we onder de 50 werknemers.
53.
Tip:
Van groeifactor naar percentage is: (groeifactor x 100) - 100
a. groeifactor = 1,23 levert: (1,23 x 100) - 100 = 23%Van groeifactor naar percentage is: (groeifactor x 100) - 100
b. De oppervlakte is verdubbeld bij 24 m2.
Bij t = 3 is de oppervlakte kroos: 12 x 1,233 = 22,33 m2 (net te weinig)
Bij t = 4 is de oppervlakte kroos: 12 x 1,234 = 27,47 m2
Dus na 4 dagen.
c. Bij welke t is de oppervlakte gelijk aan 80?
Bij t = 9 is de oppervlakte kroos: 12 x 1,239 = 77,33 m2 (net te weinig)
Bij t = 10 is de oppervlakte kroos: 12 x 1,2310 = 95,11 m2
Dus na 10 dagen.
54.
Tip:
Er is sprake van een verdubbeling als de oppervlakte gelijk is aan 12. Dus bij welke t is de oppervlakte kroos 12?
Bij t = 6 is de oppervlakte kroos: 6 x 1,126 = 11,84 m2 (net te weinig)Er is sprake van een verdubbeling als de oppervlakte gelijk is aan 12. Dus bij welke t is de oppervlakte kroos 12?
Bij t = 7 is de oppervlakte kroos: 6 x 1,127 = 13,26 m2
Dus na 7 dagen is de oppervlakte kroos verdubbeld.
55.
Tip:
Laat de formule steeds in je rekenmachine staan!
a. (0,86 x 100) - 100 = -14%Laat de formule steeds in je rekenmachine staan!
b. Na hoeveel weken is het aantal vissen gelijk aan 25?
Bij t = 4 is het aantal vissen gedaald tot: 50 x 0,864 = 27,35 vissen (net te weinig)
Bij t = 5 is het aantal vissen gedaald tot: 50 x 0,865 = 23,52 vissen
Bij t = 4,5 is het aantal vissen gedaald tot: 50 x 0,864,5 = 25,36 vissen (we zijn er bijna!)
Bij t = 4,6 is het aantal vissen gedaald tot: 50 x 0,864,6 = 24,98 vissen (we zijn er!)
Dus na 4,6 weken is de hoeveelheid vissen gehalveerd.
56.
Bij een afname van 8,2% hoort een groeifactor: (100% - 8,2%) / 100 = 0,918
Formule wordt: 1200 x 0,918t, t in jaren
Wanneer is het aantal zeeleeuwen gelijk aan 600?
Bij t = 8 krijgen we: aantal = 1200 x 0,9188 ≈ 605
Bij t = 9 krijgen we: aantal = 1200 x 0,9189 ≈ 556
Bij t = 8,1 krijgen we: aantal = 1200 x 0,9188,1 ≈ 600,08 (bijna!)
Bij t = 8,2 krijgen we: aantal = 1200 x 0,9188,2 ≈ 594,96
Dus de halveringstijd is 8,2 jaren.
57.
a. groeifactor: (100% - 11%) / 100 = 0,89
b. Formule: 100 x 0,89t
Bij t = 5 krijgen we: aantal = 100 x 0,895 ≈ 55,84
Bij t = 6 krijgen we: aantal = 100 x 0,896 ≈ 49,70
Dus de halveringstijd is 6 maanden.
58.
a. Nee, want na 3200 jaar is er nog de helft van de helft (is 1/4) over.
b. Na 1600 jaar is de hoeveelheid gehalveerd. Dus is er nog 4 kg over.
c. Na nog eens 1600 jaar is die 4 kg weer gehalveerd. Je houdt dus 2 kg over.
d. Kies: aantal kg = 8 x 0,999561600 ≈ 4. Als je formule I en II tot de macht 1600 neemt, dan gaat het naar 0. Dus geen halvering na 1600 jaar. Sterker nog: formule I heeft een halvering na 1 jaar!
59.
Tip:
groeifactor = (100% + 2,5%) / 100 = 1,025
Het bedrag na 2 jaar is: 600 x 1,0252 ≈ 630,375 eurogroeifactor = (100% + 2,5%) / 100 = 1,025
60.
Bij t = 11 krijgen we: aantal = 600 x 1,02511 ≈ 787,25 euro
Bij t = 12 krijgen we: aantal = 600 x 1,02512 ≈ 806,93 euro
Dus na 12 jaren.
61.
kies rente %: 15% dit levert: 600 x 1,152 ≈ 793,50 euro (nog net te weinig)
kies rente %: 16% dit levert: 600 x 1,162 ≈ 807,36 (net te veel) euro
kies rente %: 15,4% dit levert: 600 x 1,1542 ≈ 799,03 euro
kies rente %: 15,5% dit levert: 600 x 1,1552 ≈ 800,42 euro
Dus het rentepercentage is 15,5%
62.
Formule: b = 600 x 1,115t
Tip:
Benader het antwoord met inklemmen. Start zelf met een rente percentage. Start bijv. met 10% en kijk wat het eindbedrag is.
kies rente %: 10% dit levert: 600 x 1,102 ≈ 726 euroBenader het antwoord met inklemmen. Start zelf met een rente percentage. Start bijv. met 10% en kijk wat het eindbedrag is.
kies rente %: 15% dit levert: 600 x 1,152 ≈ 793,50 euro (nog net te weinig)
kies rente %: 16% dit levert: 600 x 1,162 ≈ 807,36 (net te veel) euro
kies rente %: 15,4% dit levert: 600 x 1,1542 ≈ 799,03 euro
kies rente %: 15,5% dit levert: 600 x 1,1552 ≈ 800,42 euro
Dus het rentepercentage is 15,5%
62.
Formule: b = 600 x 1,115t
Andere paragrafen:
1.1. Machtsverbanden (1 t/m 15)
1.2. Wortelverbanden (16 t/m 29)
1.3. Exponentiële verbanden (30 t/m 40)
1.4. Exponentiele groei en procenten (41 t/m 62)
1.5. Gemengde opgaven (63 t/m 73)
1.1. Machtsverbanden (1 t/m 15)
1.2. Wortelverbanden (16 t/m 29)
1.3. Exponentiële verbanden (30 t/m 40)
1.4. Exponentiele groei en procenten (41 t/m 62)
1.5. Gemengde opgaven (63 t/m 73)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


