TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 3.1 Van formule naar grafiek VMBO 3 KGT
Boek: Getal & Ruimte - Lineaire verbanden VMBO 3 (deel 1) opgaven 1 t/m 18, 2010Bij de woordformule: kosten abonnement = 4,50 + 0,10 x tijd is er een verband tussen de kosten en het aantal belminuten van je mobiele telefoon.
De variabelen zijn 'kosten' en 'tijd'. Want deze kunnen veranderen.
De eenheid die hoort bij 'kosten' is euro. De eenheid die hoort bij 'tijd' is minuten. Als je het aantal belminuten weet, kun je de kosten berekenen.
Van deze woordformule kunnen we een grafiek tekenen. De tijd komt op de x-as en de kosten op de y-as.
De eenheid die hoort bij 'kosten' is euro. De eenheid die hoort bij 'tijd' is minuten. Als je het aantal belminuten weet, kun je de kosten berekenen.
Van deze woordformule kunnen we een grafiek tekenen. De tijd komt op de x-as en de kosten op de y-as.
1.
a. Bij 12 uur werken, verdient ze: inkomsten = 2,61 x 12 = 31,32 euro
b. Bij 16 uur werken, verdient ze: inkomsten = 2,61 x 16 = 41,76 euro
2.
b. Bij de variabele inkomsten hoort eenheid 'euro' en bij de variabele tijd hoort eenheid 'minuten'.
3.
a. I en t
b. A en k
c. N en B
d. B en p en q
4.
b. I en t
c. Eenheden: euro en weken
d. I = 100 + 126 x 8 = 1108 euro
e. I = 100 + 126 x 13 = 1738 euro
f. Ze werkt dan 52 - 6 = 46 weken
I = 100 + 126 x 46 = 5896 euro
5.
a.
Maandloon = jaarloon / 12, dus de 12 staat voor het aantal maanden in een jaar.
Jaarloon = 52 weken x weekloon, dus 52 staat voor het aantal weken in een jaar.
45 is het vakantiegeld.
b.
M = (52w + 45) / 12
c.
Weekloon = 20 x 3 = 60
M = (52*60 + 45) / 12 = €263,75
6.
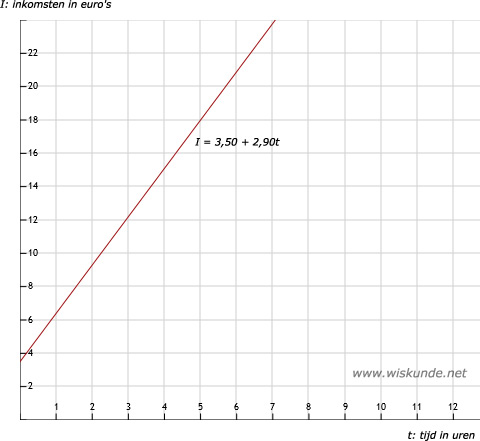
b.
Zie afbeelding
c.
Invullen t = 0 levert 3,50.
d.
De stapgrootte is 2,90.
7.
8.
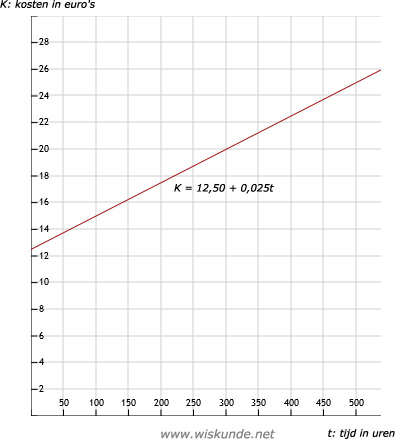
b. Er zit een scheurlijn in (zaagtand).
9.
De laatste. Want wie belt er nu meer dan 500 uur per maand?
10.
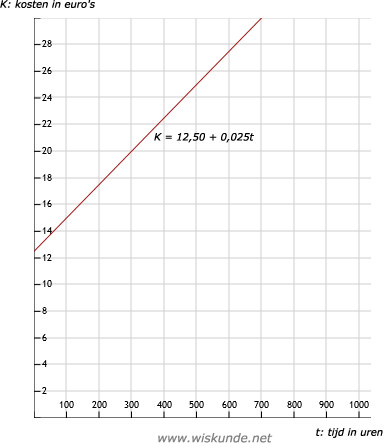
b. De stapgrootte is 0,025.
c. Ik zou nemen: 50, 100, 150, 200, 250
d. kosten = 12,50 + 0,025 x 240 = 18,50 euro
e. *
f. Zie afbeelding
a. Bij 12 uur werken, verdient ze: inkomsten = 2,61 x 12 = 31,32 euro
b. Bij 16 uur werken, verdient ze: inkomsten = 2,61 x 16 = 41,76 euro
2.
Tip:
De basis van een formule is vaak: y = ax + b, waarbij de x en y overeenkomen met de waarden op de x-as en y-as.
Bijvoorbeeld: y = 2x + 3 of verdiensten= 2,6t + 4,50
a. De formule die erbij hoort is: inkomsten = 3 x tijd, met inkomsten in euro's en tijd in urenDe basis van een formule is vaak: y = ax + b, waarbij de x en y overeenkomen met de waarden op de x-as en y-as.
Bijvoorbeeld: y = 2x + 3 of verdiensten= 2,6t + 4,50
b. Bij de variabele inkomsten hoort eenheid 'euro' en bij de variabele tijd hoort eenheid 'minuten'.
3.
Tip:
Het aantal variabelen kan ook meer dan 2 zijn. Alleen bij 2 variabelen spreken we van een lineair verband. Deze formule geeft een rechte lijn.
De variabelen zijn:Het aantal variabelen kan ook meer dan 2 zijn. Alleen bij 2 variabelen spreken we van een lineair verband. Deze formule geeft een rechte lijn.
a. I en t
b. A en k
c. N en B
d. B en p en q
4.
Tip:
We noemen 100 het 'vaste-deel' en 126xtijd het 'variabele-deel'.
a. I = 100 + 126tWe noemen 100 het 'vaste-deel' en 126xtijd het 'variabele-deel'.
b. I en t
c. Eenheden: euro en weken
d. I = 100 + 126 x 8 = 1108 euro
e. I = 100 + 126 x 13 = 1738 euro
f. Ze werkt dan 52 - 6 = 46 weken
I = 100 + 126 x 46 = 5896 euro
5.
a.
Maandloon = jaarloon / 12, dus de 12 staat voor het aantal maanden in een jaar.
Jaarloon = 52 weken x weekloon, dus 52 staat voor het aantal weken in een jaar.
45 is het vakantiegeld.
b.
M = (52w + 45) / 12
c.
Weekloon = 20 x 3 = 60
M = (52*60 + 45) / 12 = €263,75
6.
Tip:
De hoogte waar de grafiek begint is bij de 0-waarde op de x-as. Dus in dit geval bij t = 0.
a.De hoogte waar de grafiek begint is bij de 0-waarde op de x-as. Dus in dit geval bij t = 0.
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| inkomsten in euro's | €3,50 | €6,40 | €9,30 | €12,20 | €15,10 | €18,00 | €20,90 |
Zie afbeelding
c.
Invullen t = 0 levert 3,50.
d.
De stapgrootte is 2,90.

7.
Tip:
12,50 is het begingetal en 0,025 is de stapgrootte.
Kies 2 punten: (0 ; 12,50) en (300,20)
Zie afbeelding12,50 is het begingetal en 0,025 is de stapgrootte.
Kies 2 punten: (0 ; 12,50) en (300,20)

8.
Tip:
Een scheurlijn is een 'gebroken' lijntje in een as van een grafiek om aan te geven dat de schaalverdeling niet bij 0 begint. We noemen dat ook wel een zaagtand.
a. Ja, kies t = 0 en t = 20, dan zijn de kosten 12,50 en 13,00. En dat zien we ook in de grafiek.Een scheurlijn is een 'gebroken' lijntje in een as van een grafiek om aan te geven dat de schaalverdeling niet bij 0 begint. We noemen dat ook wel een zaagtand.
b. Er zit een scheurlijn in (zaagtand).
9.
De laatste. Want wie belt er nu meer dan 500 uur per maand?
10.
Tip:
Het begingetal noemen we ook wel het vaste bedrag. Want deze ligt vast.
a. Het vaste bedrag / begingetal is 12,50. Het begingetal noemen we ook wel het vaste bedrag. Want deze ligt vast.
b. De stapgrootte is 0,025.
c. Ik zou nemen: 50, 100, 150, 200, 250
d. kosten = 12,50 + 0,025 x 240 = 18,50 euro
e. *
f. Zie afbeelding

11.
12.
13.
14.
15.
b.
Na 50 seconden heeft de ballon een hoogte van 300 meter.
c. Per sec. stijgt de ballon 1,5 meter.
16.
17.
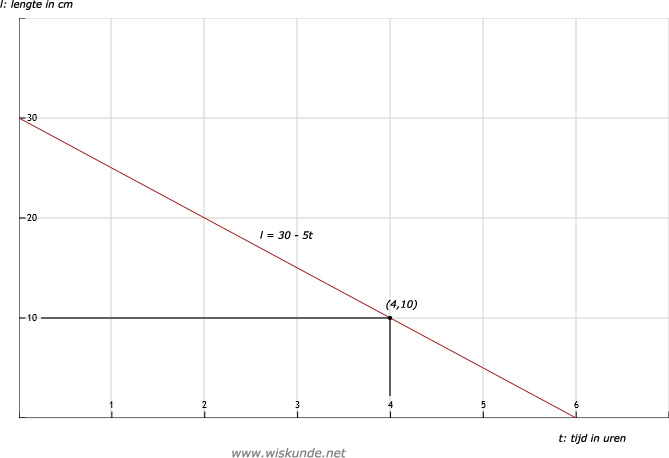
a.l = 30 - 5 x 4 = 30 - 20 = 10 cm, dus lengte van de kaars is dan nog 10 cm.
b.
c.
Het maximum is 30 cm
d.
Het minimum is 10 cm. Want dan is de kaars uit.
Dus in het plaatje hieronder zou de rode lijn moeten stoppen bij t = 4.
18.
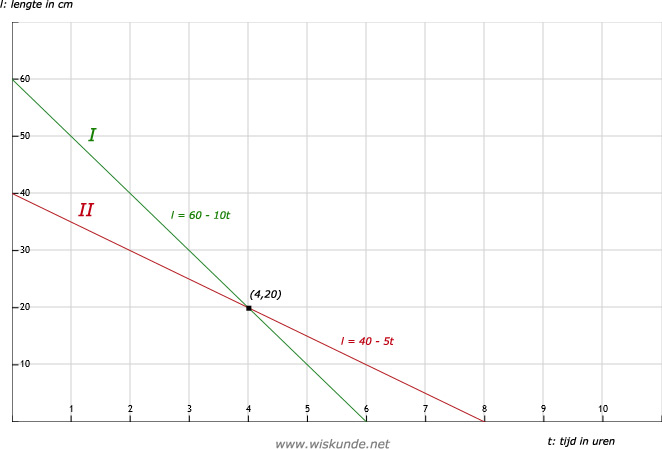
b. Maximum van de grafiek van kaars I is 60. Dat is de hoogte van de kaars bij aanvang.
c. Minimum van de grafiek van kaars II is 0. De kaars is dan opgebrand.
d. Bij het snijpunt van de 2 grafieken zijn de kaarsen even lang. Dat is bij 4 uur. Ze zijn dan beide 20 cm lang.
Tip:
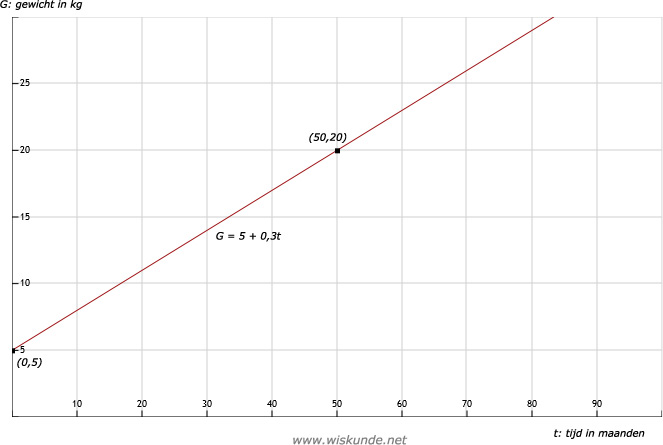
Voor een rechte lijn heb je maar 2 punten nodig. Dus (0,5) en (50,20) zou ook goed zijn.
Voor een rechte lijn heb je maar 2 punten nodig. Dus (0,5) en (50,20) zou ook goed zijn.
| tijd | 0 | 10 | 20 | 30 | 40 | 50 | 80 |
| gewicht in kilogram | 5 | 8 | 11 | 14 | 17 | 20 | 29 |

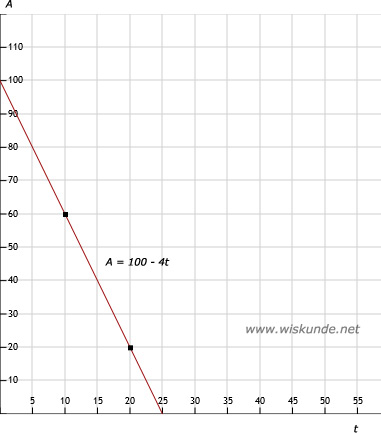
12.
Tip:
Kies 2 punten om de lijn/grafiek te tekenen. Bijvoorbeeld: (10,60) en (20,20).
Maar (0,100) en (25,0) kan natuurlijk ook.
Kies 2 punten om de lijn/grafiek te tekenen. Bijvoorbeeld: (10,60) en (20,20).
Maar (0,100) en (25,0) kan natuurlijk ook.
| t | 0 | 10 | 20 | 25 |
| A | 100 | 60 | 20 | 0 |

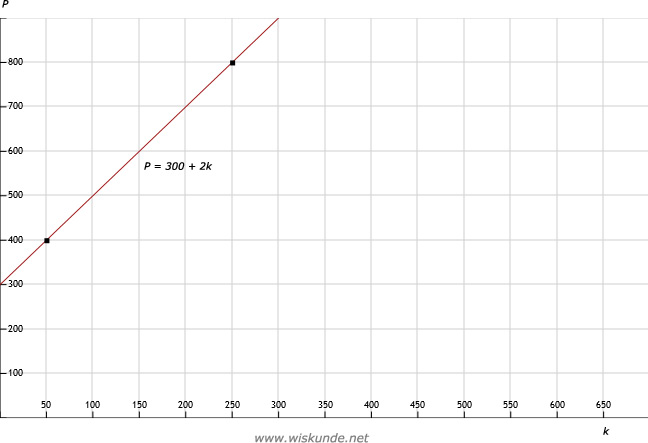
13.
Tip:
Kies 2 punten om de lijn te tekenen. Bijvoorbeeld: (50,400) en (250,800).
Bedenk (0,300) is alvast een makkelijk punt.
Kies 2 punten om de lijn te tekenen. Bijvoorbeeld: (50,400) en (250,800).
Bedenk (0,300) is alvast een makkelijk punt.
| k | 50 | 250 |
| P | 400 | 800 |

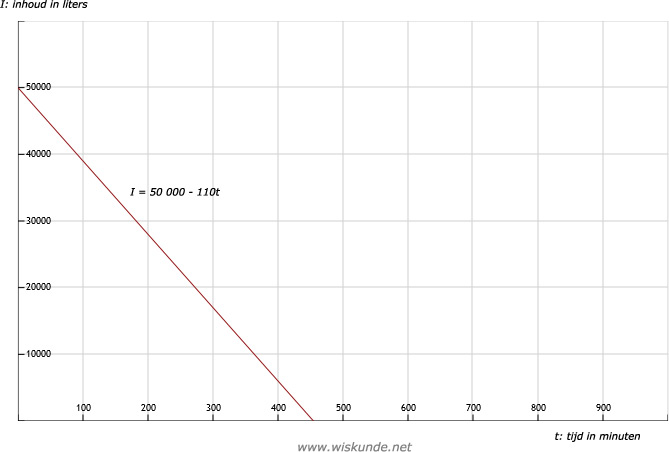
14.
Tip:
Kies 2 mooie punten om de lijn te tekenen. Bijvoorbeeld: (0,50 000) en (400,6 000).
Kies 2 mooie punten om de lijn te tekenen. Bijvoorbeeld: (0,50 000) en (400,6 000).
| t | 0 | 400 |
| Inhoud in liters | 50 000 | 6 000 |

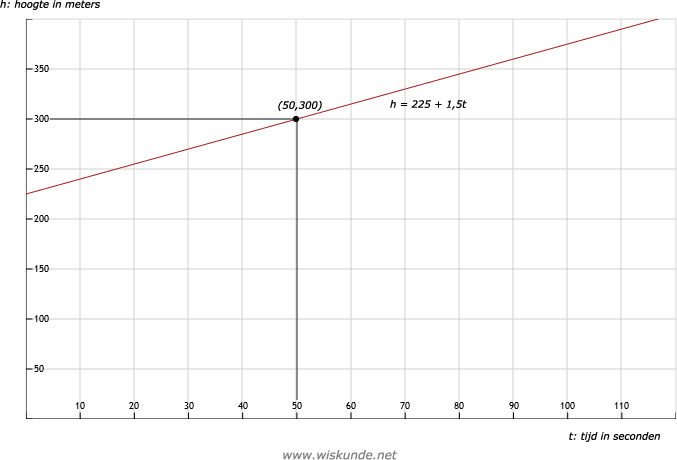
15.
Tip:
Kies 2 mooie punten om de lijn te tekenen. Bijvoorbeeld: (0,225) en (100,375).
a.Kies 2 mooie punten om de lijn te tekenen. Bijvoorbeeld: (0,225) en (100,375).
| Tijd in sec. | 0 | 50 | 100 |
| Hoogte in meters | 225 | 300 | 375 |
Na 50 seconden heeft de ballon een hoogte van 300 meter.
c. Per sec. stijgt de ballon 1,5 meter.

16.
Tip:
2 minuten = 120 sec. In de formule moet je seconden invullen en niet minuten.
120 seconden invullen levert: h = 225 + 1,5 x 120 = 4052 minuten = 120 sec. In de formule moet je seconden invullen en niet minuten.
17.
a.l = 30 - 5 x 4 = 30 - 20 = 10 cm, dus lengte van de kaars is dan nog 10 cm.
b.
| Tijd in sec. | 0 | 4 | 6 |
| Hoogte in meters | 30 | 10 | 0 |
c.
Het maximum is 30 cm
d.
Het minimum is 10 cm. Want dan is de kaars uit.
Dus in het plaatje hieronder zou de rode lijn moeten stoppen bij t = 4.

18.
Tip:
Je hebt 2 punten nodig om een rechte lijn te tekenen. Met het begingetal van de formule heb je al 1 punt. Dat is namelijk het snijpunt met de y-as.
a. Zie afbeeldingJe hebt 2 punten nodig om een rechte lijn te tekenen. Met het begingetal van de formule heb je al 1 punt. Dat is namelijk het snijpunt met de y-as.
b. Maximum van de grafiek van kaars I is 60. Dat is de hoogte van de kaars bij aanvang.
c. Minimum van de grafiek van kaars II is 0. De kaars is dan opgebrand.
d. Bij het snijpunt van de 2 grafieken zijn de kaarsen even lang. Dat is bij 4 uur. Ze zijn dan beide 20 cm lang.

Andere paragrafen:
3.1. Van formule naar grafiek (1 t/m 18)
3.2. Gelijkmatige toename of afname (19 t/m 27)
3.3. Van tabel naar formule (28 t/m 37)
3.4. Van grafiek naar formule (38 t/m 43)
3.5. Stapgrootte (44 t/m 56)
3.1. Van formule naar grafiek (1 t/m 18)
3.2. Gelijkmatige toename of afname (19 t/m 27)
3.3. Van tabel naar formule (28 t/m 37)
3.4. Van grafiek naar formule (38 t/m 43)
3.5. Stapgrootte (44 t/m 56)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


