TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 3.2 Gelijkmatige toename of afname VMBO 3 KGT
Boek: Getal & Ruimte - Lineaire verbanden VMBO 3 (deel 1) opgaven 19 t/m 27, 2010Wanneer is er sprake van een gelijkmatige toename?
Als de toename in de bovenste rij van een tabel gelijkmatig is (bijvoorbeeld steeds +1) en de toename in de onderste rij van een tabel ook (bijvoorbeeld +7) dan spreken we van een gelijkmatige toename.
Als de onderste rij met een zelfde waarde afneemt, spreken we van een gelijkmatige afname.
Als de toename in de bovenste rij van een tabel gelijkmatig is (bijvoorbeeld steeds +1) en de toename in de onderste rij van een tabel ook (bijvoorbeeld +7) dan spreken we van een gelijkmatige toename.
Als de onderste rij met een zelfde waarde afneemt, spreken we van een gelijkmatige afname.
19.
a. Er zit een gelijkmatige toename bij tabel 2.
b. Als t met 1 stijgt in tabel 2, dan stijgt l met 25.
c. Als t met 1 stijgt in tabel 1, dan stijgt l met de ene keer 5 en de andere keer 15.
20.
30/1 = 30
40/2 = 20
70/4 = 17,5
De uitkomsten zijn niet gelijk, dus er is geen sprake van een gelijkmatige toename.
b.
Er is dus geen stapgrootte.
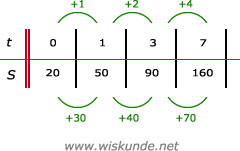
21.
-10/10 = -1
-20/20 = -1
-30/30 = -1
De uitkomsten zijn gelijk, dus er is sprake van een gelijkmatige afname.
b.
Stapgrootte = -1
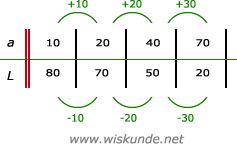
22.
60/4 = 15
30/2 = 15
35/3 = 11,7
De uitkomsten zijn niet gelijk, dus er is geen sprake van een gelijkmatige toename.
b.
Er is dus geen stapgrootte.
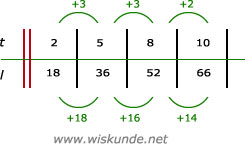
23.
a.
18/3 = 6
16/3 = 5,3
14/2 = 7
De uitkomsten zijn niet gelijk, dus er is geen sprake van een gelijkmatige toename.
b.
Er is dus geen stapgrootte.
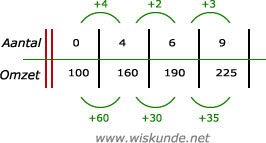
24.
b. Bij D. Want boven +5 dan onder -250.
25.
a.
A heeft een gelijkmatige afname.
B heeft een gelijkmatige toename.
C heeft een gelijkmatige toename.
D heeft een gelijkmatige toename.
b.
A heeft stapgrootte -0,1.
B heeft stapgrootte 2.
C heeft stapgrootte 15.
D heeft stapgrootte 16.
26.
Bovenste rij: +3 +4 +2
Onderste rij: -54 -72 -36
Stapgrootte:
-54/3 = -18
-72/4 = -18
-36/2 = -18
De uitkomsten zijn gelijk dus er is sprake van een gelijkmatige afname met stapgrootte -18.
Bij B:
Bovenste rij: +4 +2 +2
Onderste rij: +24 +12 +12
Stapgrootte:
24/4 = 6
12/2 = 6
12/2 = 6
De uitkomsten zijn gelijk dus er is sprake van een gelijkmatige toename met stapgrootte 6.
27.
Bovenste rij: +6 +9 +9 +6
Onderste rij: -7500 -11250 -9250 -2000
Stapgrootte:
-7500/6 = -1250
-11250/9 = -1250
-9250/9 = -1027,8
-2000/6 = -333,3
De uitkomsten zijn niet gelijk dus er is geen gelijkmatige afname en dus ook geen stapgrootte.
a. Er zit een gelijkmatige toename bij tabel 2.
b. Als t met 1 stijgt in tabel 2, dan stijgt l met 25.
c. Als t met 1 stijgt in tabel 1, dan stijgt l met de ene keer 5 en de andere keer 15.
20.
Tip:
stapgrootte = toename onder / toename boven levert:
a.stapgrootte = toename onder / toename boven levert:
30/1 = 30
40/2 = 20
70/4 = 17,5
De uitkomsten zijn niet gelijk, dus er is geen sprake van een gelijkmatige toename.
b.
Er is dus geen stapgrootte.

21.
Tip:
Zet onderstaande punten (van de tabel) maar eens in een grafiek. Je zult zien dat ze dan op een rechte lijn liggen.
a.Zet onderstaande punten (van de tabel) maar eens in een grafiek. Je zult zien dat ze dan op een rechte lijn liggen.
-10/10 = -1
-20/20 = -1
-30/30 = -1
De uitkomsten zijn gelijk, dus er is sprake van een gelijkmatige afname.
b.
Stapgrootte = -1

22.
Tip:
De tabel "zou je kunnen zien" als boven +1 en dan onder +15. Op het eind gaat dat net mis.
Zou er sprake zijn van een gelijkmatige toename als er 235 had gestaan i.p.v. 225? Antwoord: Ja.
a.De tabel "zou je kunnen zien" als boven +1 en dan onder +15. Op het eind gaat dat net mis.
Zou er sprake zijn van een gelijkmatige toename als er 235 had gestaan i.p.v. 225? Antwoord: Ja.
60/4 = 15
30/2 = 15
35/3 = 11,7
De uitkomsten zijn niet gelijk, dus er is geen sprake van een gelijkmatige toename.
b.
Er is dus geen stapgrootte.

23.
a.
18/3 = 6
16/3 = 5,3
14/2 = 7
De uitkomsten zijn niet gelijk, dus er is geen sprake van een gelijkmatige toename.
b.
Er is dus geen stapgrootte.

24.
Tip:
Zet bij tabel B de boven waarden op volgorde. Dan zie je het beter.
a. Bij A. Want boven +1 dan onder +2.Zet bij tabel B de boven waarden op volgorde. Dan zie je het beter.
b. Bij D. Want boven +5 dan onder -250.
25.
a.
A heeft een gelijkmatige afname.
B heeft een gelijkmatige toename.
C heeft een gelijkmatige toename.
D heeft een gelijkmatige toename.
b.
A heeft stapgrootte -0,1.
B heeft stapgrootte 2.
C heeft stapgrootte 15.
D heeft stapgrootte 16.
26.
Tip:
Bepaal de stappen in de bovenste- en onderste rij en deel deze op elkaar. Zijn de uitkomsten gelijk? Dan is dat de stapgrootte en is er sprake van een gelijkmatige toe- of afname.
Bij A:Bepaal de stappen in de bovenste- en onderste rij en deel deze op elkaar. Zijn de uitkomsten gelijk? Dan is dat de stapgrootte en is er sprake van een gelijkmatige toe- of afname.
Bovenste rij: +3 +4 +2
Onderste rij: -54 -72 -36
Stapgrootte:
-54/3 = -18
-72/4 = -18
-36/2 = -18
De uitkomsten zijn gelijk dus er is sprake van een gelijkmatige afname met stapgrootte -18.
Bij B:
Bovenste rij: +4 +2 +2
Onderste rij: +24 +12 +12
Stapgrootte:
24/4 = 6
12/2 = 6
12/2 = 6
De uitkomsten zijn gelijk dus er is sprake van een gelijkmatige toename met stapgrootte 6.
27.
Bovenste rij: +6 +9 +9 +6
Onderste rij: -7500 -11250 -9250 -2000
Stapgrootte:
-7500/6 = -1250
-11250/9 = -1250
-9250/9 = -1027,8
-2000/6 = -333,3
De uitkomsten zijn niet gelijk dus er is geen gelijkmatige afname en dus ook geen stapgrootte.
Andere paragrafen:
3.1. Van formule naar grafiek (1 t/m 18)
3.2. Gelijkmatige toename of afname (19 t/m 27)
3.3. Van tabel naar formule (28 t/m 37)
3.4. Van grafiek naar formule (38 t/m 43)
3.5. Stapgrootte (44 t/m 56)
3.1. Van formule naar grafiek (1 t/m 18)
3.2. Gelijkmatige toename of afname (19 t/m 27)
3.3. Van tabel naar formule (28 t/m 37)
3.4. Van grafiek naar formule (38 t/m 43)
3.5. Stapgrootte (44 t/m 56)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


