TIP: Wil je ook toegang tot meer dan 16.900 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 1.2 Lineaire formules opstellen HAVO 3
Boek: Getal & Ruimte - Lineaire problemen HAVO 3 (deel 1) opgaven 13 t/m 28, 2010Hoe stel je de formule van een lijn op?
De basisvorm van een lineaire lijn is: y = ax + b. Waarbij a de richtingscoëfficient is en b de snijpunt met de y-as (met x = 0). Zoek dus het snijpunt met de y-as (0,b) en vul dat in voor b. Een richtingscoëfficient van 3 wil zeggen: 1 naar rechts en 3 omhoog. Een richtingscoëfficient van -2 wil zeggen: 1 naar rechts en 2 omlaag.
Stel dat de richtingscoëfficient gelijk is aan 4 en het snijpunt met de y-as is (0,5) dan wordt de formule y = 4x + 5.
De basisvorm van een lineaire lijn is: y = ax + b. Waarbij a de richtingscoëfficient is en b de snijpunt met de y-as (met x = 0). Zoek dus het snijpunt met de y-as (0,b) en vul dat in voor b. Een richtingscoëfficient van 3 wil zeggen: 1 naar rechts en 3 omhoog. Een richtingscoëfficient van -2 wil zeggen: 1 naar rechts en 2 omlaag.
Stel dat de richtingscoëfficient gelijk is aan 4 en het snijpunt met de y-as is (0,5) dan wordt de formule y = 4x + 5.
13.
a. a = 6 en b = 20
b. a = -8 en b = -200
c. a = 1 en b = 8
d. a = -1 en b = 10
e. a = 1/3 en b = 0
f. a = -1 en b = 0
14.
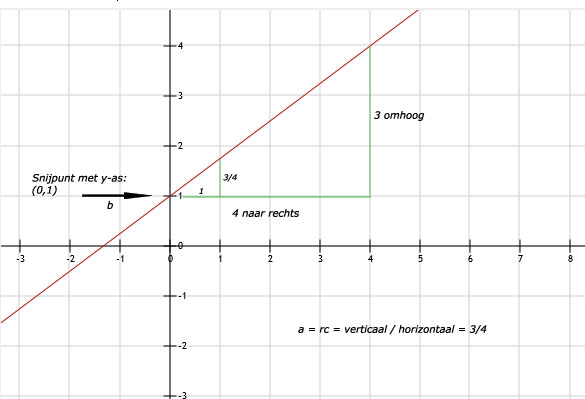
a. Snijpunt met de y-as is (0,1). Dus b = 1.
b. De grafiek gaat 4 naar rechts en 3 omhoog. Ofwel 1 naar rechts en 3/4 omhoog. Dus a = 3/4.
c. De formule van deze lijn wordt dan: y = 3/4x + 1
15.
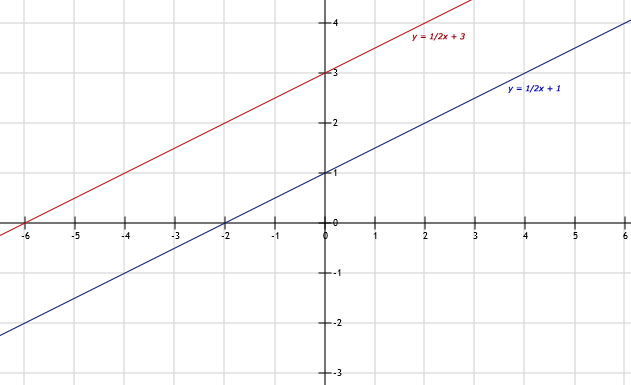
De formule van lijn l: is: y = x + 2
De formule van lijn m: is: y = -1½x + 1
De formule van lijn n: is: y = -1/3x + 4
b. De formule van lijn k: is: y = -1/3x - 3
16.
De formule van lijn q: is: y = ½x - 1½
De formule van lijn r: is: y = -2x
17.
a. b = 200
b. De lijn gaat door (0,200) en (50,400). Dus a = rc = verticaal / horizontaal = 200 / 50 = 4
c. De formule van de lijn is: N = 4t + 200
18.
b. De formule van lijn k: is: B = -6 2/3 + 250
c. De formule van lijn m: is: B = -5t + 150
19.
a. N = -3t + 152
b. t = 28 geeft N = 68 ziekenhuizen
20.
b. B = 5t + 7,50
c. B = 3k + 8
d. B = 1850 - 150t
21.
a. Omdat er ieder jaar steeds een gelijke daling is van 3000 bedrijven.
b. Aantal bedrijven op 1 januari zou kunnen zijn: 92 + 3 + 3 -> 98 000
c. 3 000
d. N = -3t + 98
e. *
22.
b. Zie afbeelding: 2 punten: (0,1) en (2,2)
c. Snijpunt y-as is (0,b) dus ze heeft voor 8 gekozen.
d. Grafiek door (8,0) dus invullen levert: y = 1/2 x 8 + b = 4 + b.
4 + b = 0 levert b = -4. Ze heeft dus voor -4 gekozen.
a. a = 6 en b = 20
b. a = -8 en b = -200
c. a = 1 en b = 8
d. a = -1 en b = 10
e. a = 1/3 en b = 0
f. a = -1 en b = 0
14.
a. Snijpunt met de y-as is (0,1). Dus b = 1.
b. De grafiek gaat 4 naar rechts en 3 omhoog. Ofwel 1 naar rechts en 3/4 omhoog. Dus a = 3/4.
c. De formule van deze lijn wordt dan: y = 3/4x + 1

15.
Tip:
Lijnen die evenwijdig zijn, hebben dezelfde richtingscoëfficient. Dus dezelfde 'a'.
a. Lijnen die evenwijdig zijn, hebben dezelfde richtingscoëfficient. Dus dezelfde 'a'.
De formule van lijn l: is: y = x + 2
De formule van lijn m: is: y = -1½x + 1
De formule van lijn n: is: y = -1/3x + 4
b. De formule van lijn k: is: y = -1/3x - 3
16.
Tip:
a = rc = verticaal / horizontaal
De formule van lijn p: is: y = -2/5x + 3a = rc = verticaal / horizontaal
De formule van lijn q: is: y = ½x - 1½
De formule van lijn r: is: y = -2x
17.
a. b = 200
b. De lijn gaat door (0,200) en (50,400). Dus a = rc = verticaal / horizontaal = 200 / 50 = 4
c. De formule van de lijn is: N = 4t + 200
18.
Tip:
Bij a. : Neem om rc te bepalen de punten (0,50) en (20,100).
a. a = rc = verticaal / horizontaal = 50 / 20 = 2,5, tevens b = 50Bij a. : Neem om rc te bepalen de punten (0,50) en (20,100).
b. De formule van lijn k: is: B = -6 2/3 + 250
c. De formule van lijn m: is: B = -5t + 150
19.
a. N = -3t + 152
b. t = 28 geeft N = 68 ziekenhuizen
20.
Tip:
B = at + b, dan is t het variabele deel en b het vaste- of constante deel.
a. B = 25t + 15B = at + b, dan is t het variabele deel en b het vaste- of constante deel.
b. B = 5t + 7,50
c. B = 3k + 8
d. B = 1850 - 150t
21.
a. Omdat er ieder jaar steeds een gelijke daling is van 3000 bedrijven.
b. Aantal bedrijven op 1 januari zou kunnen zijn: 92 + 3 + 3 -> 98 000
c. 3 000
d. N = -3t + 98
e. *
22.
Tip:
Om een rechte lijn te tekenen, heb je genoeg aan 2 punten. Vul x = 0 in en je hebt dan meteen al het snijpunt met de y-as. Als 1e punt x = 0 kiezen, is altijd de gemakkelijkste.
a. Zie afbeelding: 2 punten: (0,3) en (2,4)Om een rechte lijn te tekenen, heb je genoeg aan 2 punten. Vul x = 0 in en je hebt dan meteen al het snijpunt met de y-as. Als 1e punt x = 0 kiezen, is altijd de gemakkelijkste.
b. Zie afbeelding: 2 punten: (0,1) en (2,2)
c. Snijpunt y-as is (0,b) dus ze heeft voor 8 gekozen.
d. Grafiek door (8,0) dus invullen levert: y = 1/2 x 8 + b = 4 + b.
4 + b = 0 levert b = -4. Ze heeft dus voor -4 gekozen.

23.
24.
12 = 2 ⋅ 8 + b
b = -4
Dus: b = -4
25.
b = 0,5
26.
27.
28.
a. Formule van lijn m: y = -2½x + 28
b. Formule van lijn n: y = -x + 4⅓
Tip:
Lijnen die evenwijdig zijn, hebben dezelfde richtingscoëfficient. Dus dezelfde 'a'.
Hij heeft 8 gekozen.Lijnen die evenwijdig zijn, hebben dezelfde richtingscoëfficient. Dus dezelfde 'a'.
24.
Tip:
Vul het punt A(8,12) in en je krijgt b. Bij (8,12) is de x gelijk aan 8 en de y gelijk aan 12.
(x,y) <-> (8,12)
y = 2x + bVul het punt A(8,12) in en je krijgt b. Bij (8,12) is de x gelijk aan 8 en de y gelijk aan 12.
(x,y) <-> (8,12)
12 = 2 ⋅ 8 + b
b = -4
Dus: b = -4
25.
b = 0,5
26.
Tip:
Evenwijdig dus a = rck = rcl = 5, om b te bepalen vul P(1,6) in y = 5x + b.
a = 5 en b = 1, dus de formule van lijn k: is y = 5x + 1.Evenwijdig dus a = rck = rcl = 5, om b te bepalen vul P(1,6) in y = 5x + b.
27.
Tip:
Evenwijdig dus a = rcp = rcq = -2, om b te bepalen vul S(-5,-1) in y = -2x + b.
a = -2 en b = -11, dus de formule van lijn p: is y = -2x - 11.Evenwijdig dus a = rcp = rcq = -2, om b te bepalen vul S(-5,-1) in y = -2x + b.
28.
a. Formule van lijn m: y = -2½x + 28
b. Formule van lijn n: y = -x + 4⅓
Andere paragrafen:
1.1. Lineaire formules (1 t/m 12)
1.2. Lineaire formules opstellen (13 t/m 28)
1.3. Lineaire vergelijkingen (29 t/m 47)
1.4. Lineaire functies (48 t/m 57)
1.5. Snijpunten van grafieken (58 t/m 68)
1.1. Lineaire formules (1 t/m 12)
1.2. Lineaire formules opstellen (13 t/m 28)
1.3. Lineaire vergelijkingen (29 t/m 47)
1.4. Lineaire functies (48 t/m 57)
1.5. Snijpunten van grafieken (58 t/m 68)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


