TIP: Wil je ook toegang tot meer dan 16.900 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 1.5 Snijpunten van grafieken HAVO 3
Boek: Getal & Ruimte - Lineaire problemen HAVO 3 (deel 1) opgaven 58 t/m 68, 2010Hoe berekenen we de snijpunten met de assen?
- snijpunt met de x-as: y-coördinaat is 0 en de x-coördinaat krijgen we door f(x) = 0 op te lossen
- snijpunt met de y-as: x-coördinaat is 0 en de y-coördinaat krijgen we door f(0) op te lossen (of x = 0 in te vullen)
Hoe berekenen we het snijpunt tussen 2 grafieken?
Stel de 2 grafieken aan elkaar gelijk en los op: f(x) = g(x). De uitkomst van deze vergelijking is de x-coördinaat van het snijpunt.
De y-coördinaat van het snijpunt krijgen we door de x in te vullen in 1 van de 2 vergelijkingen.
- snijpunt met de x-as: y-coördinaat is 0 en de x-coördinaat krijgen we door f(x) = 0 op te lossen
- snijpunt met de y-as: x-coördinaat is 0 en de y-coördinaat krijgen we door f(0) op te lossen (of x = 0 in te vullen)
Hoe berekenen we het snijpunt tussen 2 grafieken?
Stel de 2 grafieken aan elkaar gelijk en los op: f(x) = g(x). De uitkomst van deze vergelijking is de x-coördinaat van het snijpunt.
De y-coördinaat van het snijpunt krijgen we door de x in te vullen in 1 van de 2 vergelijkingen.
58.
a. Als een punt op de x-as ligt dan is de y-coördinaat gelijk aan 0. Bijvoorbeeld (3,0) ligt op de x-as en de y is 0.
Als een punt op de y-as ligt dan is de x-coördinaat gelijk aan 0. Bijvoorbeeld (0,3) ligt op de y-as en de x is 0.
b. f(0) = 2 en het snijpunt met de y-as is (0,2).
c. f(4) = 0 en het snijpunt met de x-as is (4,0).
59.
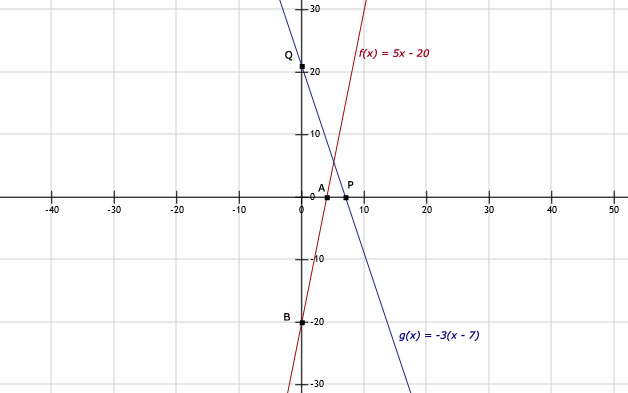
a. Snijpunt x-as: Los op: f(x) = 0 levert x = 4. Dus snijpunt A met de x-as is (4,0).
Snijpunt y-as: Los op: f(0) levert y = -20. Dus snijpunt B met de y-as is (0,-20).
b. Snijpunt x-as: Los op: g(x) = 0 levert x = 7. Dus snijpunt P met de x-as is (7,0).
Snijpunt y-as: Los op: g(0) levert y = 21. Dus snijpunt Q met de y-as is (0,21).
60.
A(0 ; -0,9)
B(0,75 ; 0)
C(0 ; 6,3)
D(3,5 ; 0)
61.
b. y = ax + 8, door B(-2,0) geeft 0 = -2a + 8. Hieruit volgt dat a = 4.
62.
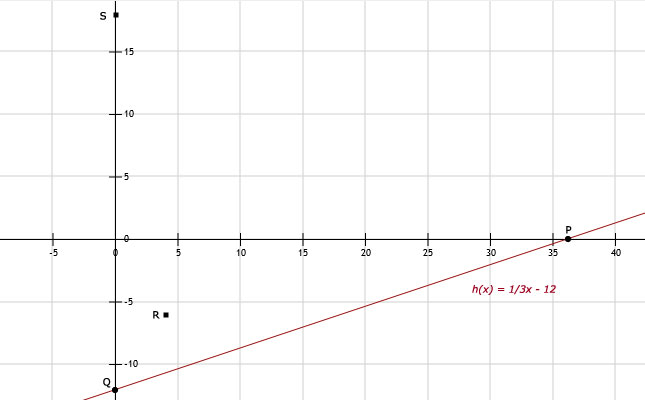
Snijpunt met de y-as => x = 0 levert Q(0,-12)
a. Stel lijn: y = ax + b
De lijn door Q en R heeft a = rc = verticaal / horizontaal = 6/4 = 1,5
Door (0,-12) levert b = -12
Vergelijking van de lijn door Q en R: y = 1,5x - 12
b. Stel lijn: y = ax + b
De lijn door P en S heeft a = rc = verticaal / horizontaal = -18/36 = -1/2
Door (0,18) levert b = 18
Vergelijking van de lijn door P en S: y = -1/2x + 18
63.
a. f(1) = 5 en g(1) = 5
b. Je hebt nu de coördinaten gevonden van het snijpunt van f(x) en g(x). Dat is dus B(1,5).
64.
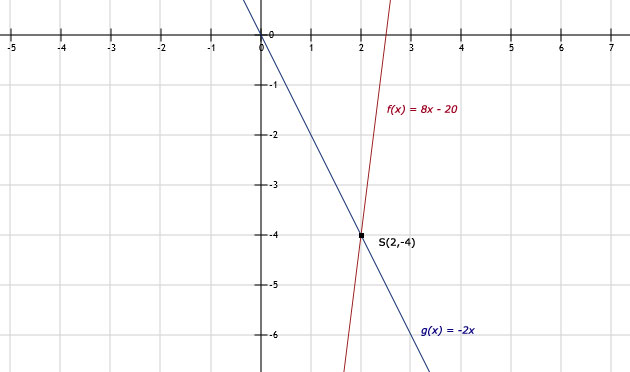
8x - 20 = -2x
10x = 20
x = 2
Invullen in de formule geeft: y = -4
Het snijpunt is dus S(2,-4)
65.
f(x) = g(x) levert:
0,8x - 3,7 = -1,6x + 2,9
2,4x = 6,6
x = 6,6 / 2,4 = 2,75
Invullen in de formule geeft: y = -1,5
Het snijpunt is dus A(2,75 ; -1,5)
66.
B(0,2)
C(1½,3½)
67.
A(-6,0)
B(10,0)
S(-2,6)
a. Als een punt op de x-as ligt dan is de y-coördinaat gelijk aan 0. Bijvoorbeeld (3,0) ligt op de x-as en de y is 0.
Als een punt op de y-as ligt dan is de x-coördinaat gelijk aan 0. Bijvoorbeeld (0,3) ligt op de y-as en de x is 0.
b. f(0) = 2 en het snijpunt met de y-as is (0,2).
c. f(4) = 0 en het snijpunt met de x-as is (4,0).
59.
a. Snijpunt x-as: Los op: f(x) = 0 levert x = 4. Dus snijpunt A met de x-as is (4,0).
Snijpunt y-as: Los op: f(0) levert y = -20. Dus snijpunt B met de y-as is (0,-20).
b. Snijpunt x-as: Los op: g(x) = 0 levert x = 7. Dus snijpunt P met de x-as is (7,0).
Snijpunt y-as: Los op: g(0) levert y = 21. Dus snijpunt Q met de y-as is (0,21).

60.
Tip:
Snijpunt x-as -> y = 0 en bij snijpunt y-as -> x = 0.
De coördinaten van de snijpunten met de assen zijn:Snijpunt x-as -> y = 0 en bij snijpunt y-as -> x = 0.
A(0 ; -0,9)
B(0,75 ; 0)
C(0 ; 6,3)
D(3,5 ; 0)
61.
Tip:
Vul het punt in de vergelijking en bepaal zo a en b.
a. y = -x + b, door A(8,0) geeft 0 = -8 + b. Hieruit volgt dat b = 8.Vul het punt in de vergelijking en bepaal zo a en b.
b. y = ax + 8, door B(-2,0) geeft 0 = -2a + 8. Hieruit volgt dat a = 4.
62.
Tip:
Bedenk bij de formule van een lijn: y = ax + b:
a = rc = verticaal / horizontaal
Bepaal eerst de snijpunten met de x-as en y-as. Snijpunt met de x-as => y = 0 levert P(36,0).Bedenk bij de formule van een lijn: y = ax + b:
a = rc = verticaal / horizontaal
Snijpunt met de y-as => x = 0 levert Q(0,-12)
a. Stel lijn: y = ax + b
De lijn door Q en R heeft a = rc = verticaal / horizontaal = 6/4 = 1,5
Door (0,-12) levert b = -12
Vergelijking van de lijn door Q en R: y = 1,5x - 12
b. Stel lijn: y = ax + b
De lijn door P en S heeft a = rc = verticaal / horizontaal = -18/36 = -1/2
Door (0,18) levert b = 18
Vergelijking van de lijn door P en S: y = -1/2x + 18

63.
a. f(1) = 5 en g(1) = 5
b. Je hebt nu de coördinaten gevonden van het snijpunt van f(x) en g(x). Dat is dus B(1,5).
64.
Tip:
Gebruik f(x) = g(x) om de coördinaten te berekenen van het snijpunt S.
f(x) = g(x) levert:Gebruik f(x) = g(x) om de coördinaten te berekenen van het snijpunt S.
8x - 20 = -2x
10x = 20
x = 2
Invullen in de formule geeft: y = -4
Het snijpunt is dus S(2,-4)

65.
f(x) = g(x) levert:
0,8x - 3,7 = -1,6x + 2,9
2,4x = 6,6
x = 6,6 / 2,4 = 2,75
Invullen in de formule geeft: y = -1,5
Het snijpunt is dus A(2,75 ; -1,5)
66.
Tip:
snijpunt x-as: y = 0 -> f(x) = 0
snijpunt y-as: x = 0 -> f(0)
snijpunt 2 grafieken: f(x) = g(x)
A(⅓,0)snijpunt x-as: y = 0 -> f(x) = 0
snijpunt y-as: x = 0 -> f(0)
snijpunt 2 grafieken: f(x) = g(x)
B(0,2)
C(1½,3½)
67.
A(-6,0)
B(10,0)
S(-2,6)
68.
Je hebt 2 lijnen: y = px + q en y = qx + 4
y = qx + 4 door (-1,8) levert:
8 = -q + 4
q = -4
y = px + q door (-1,8) levert:
8 = -p + q
Vul q = -4 in levert: 8 = -p - 4 => p = -12
Je hebt 2 lijnen: y = px + q en y = qx + 4
y = qx + 4 door (-1,8) levert:
8 = -q + 4
q = -4
y = px + q door (-1,8) levert:
8 = -p + q
Vul q = -4 in levert: 8 = -p - 4 => p = -12
Andere paragrafen:
1.1. Lineaire formules (1 t/m 12)
1.2. Lineaire formules opstellen (13 t/m 28)
1.3. Lineaire vergelijkingen (29 t/m 47)
1.4. Lineaire functies (48 t/m 57)
1.5. Snijpunten van grafieken (58 t/m 68)
1.1. Lineaire formules (1 t/m 12)
1.2. Lineaire formules opstellen (13 t/m 28)
1.3. Lineaire vergelijkingen (29 t/m 47)
1.4. Lineaire functies (48 t/m 57)
1.5. Snijpunten van grafieken (58 t/m 68)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


