TIP: Wil je ook toegang tot meer dan 17.800 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 1.3 Lineaire vergelijkingen HAVO 3
Boek: Getal & Ruimte - Lineaire problemen HAVO 3 (deel 1) opgaven 29 t/m 47, 2010Hoe lossen we een lineaire vergelijking op?
Je brengt eerst alle x-en naar de linkerkant (linkerlid). Dan zorg je ervoor dat alle getallen naar de rechterkant gaan (rechterlid).
Deel daarna links en rechts door het getal voor de x. Als er haakjes staan, dan dien je deze eerst weg te werken.
Als er in een lineaire vergelijking breuken staan, dan vermenigvuldig je links en rechts met hetzelfde getal.
Voorbeelden van lineaire vergelijkingen: 8x – 12 = 4x – 21 of 5(x - 3) = 3(x - 7)
Je brengt eerst alle x-en naar de linkerkant (linkerlid). Dan zorg je ervoor dat alle getallen naar de rechterkant gaan (rechterlid).
Deel daarna links en rechts door het getal voor de x. Als er haakjes staan, dan dien je deze eerst weg te werken.
Als er in een lineaire vergelijking breuken staan, dan vermenigvuldig je links en rechts met hetzelfde getal.
Voorbeelden van lineaire vergelijkingen: 8x – 12 = 4x – 21 of 5(x - 3) = 3(x - 7)
29.
b. 5x
c. 2x
d. -2x - 6
e. -12x - 9
f. -16x - 9
30.
a. 3x + 5 = -2x + 8 geeft 3x + 2x = 8 - 5, dit levert: 5x = 3
b. 6x - 3 = 4x + 7 geeft 6x - 4x = 7 + 3, dit levert: 2x = 10
c. -8x - 13 = 5x geeft -8x - 5x = 13, dit levert: -13x = 13
d. 3x - 12 = 5x + 8 - x geeft 3x - 5x + x = 8 + 12, dit levert: -x = 20
31.
a. 5x - 2x = -8 - 11
b. -3x - 5x = 12
c. 7x + 5x = 5 + 19
d. -1/2x - 3x = -6
32.
I hoort bij a
II hoort bij h
III hoort bij g
IV hoort bij f
33.
b. 7x - 6x = 8 - 3 geeft x = 5
c. -4x = 10 geeft x = -2½
d. 7x = -14 geeft x = -2
34.
a. -7x = 0 geeft x = 0
b. -y + 2y = 5 + 1 geeft y = 6
c. 8x = -16 geeft x = -2
d. -3a = -13 geeft a = 4⅓
35.
b. 3p - 4p = -9 + 1 geeft -p = -8 dus p = 8
c. 3q - 8q + 3q = -2 + 2 geeft -2q = 0 dus q = 0
d. 5a - 4a + 2a = 6 geeft 3a = 6 dus a = 2
36.
b. -2(6 - x) = -12 + 2x
c. -(x - 8) = -x + 8
d. -¼(3x + 12) = -¾x - 3
37.
b. 3p = 21 levert p = 7
c. 4x = 15 levert x = 3 3/4
d. -x = -10 levert x = 10
38.
a. 7x - 6x = -6 - 3 levert x = -9
b. 4x - 5x = -5 + 16 levert x = -11
c. -2x = -30 levert x = 15
d. 3x - 5x = 3 - 3 levert x = 0
Tip:
3x en 4x zijn gelijksoortig. Daarom mag je deze optellen tot 7x. Bedenk dat 3x en 4y niet gelijksoortig zijn.
a. 13x3x en 4x zijn gelijksoortig. Daarom mag je deze optellen tot 7x. Bedenk dat 3x en 4y niet gelijksoortig zijn.
b. 5x
c. 2x
d. -2x - 6
e. -12x - 9
f. -16x - 9
30.
a. 3x + 5 = -2x + 8 geeft 3x + 2x = 8 - 5, dit levert: 5x = 3
b. 6x - 3 = 4x + 7 geeft 6x - 4x = 7 + 3, dit levert: 2x = 10
c. -8x - 13 = 5x geeft -8x - 5x = 13, dit levert: -13x = 13
d. 3x - 12 = 5x + 8 - x geeft 3x - 5x + x = 8 + 12, dit levert: -x = 20
31.
a. 5x - 2x = -8 - 11
b. -3x - 5x = 12
c. 7x + 5x = 5 + 19
d. -1/2x - 3x = -6
32.
I hoort bij a
II hoort bij h
III hoort bij g
IV hoort bij f
33.
Tip:
Een lineaire vergelijking los je op door termen van de ene naar de andere kant te brengen. Dus x-en links en de getallen rechts. Deel uiteindelijk beide leden door het getal voor de x. Zo vind je de oplossing. Ter controle vul de oplossing in en kijk of het klopt.
a. -3x = -3 geeft x = 1Een lineaire vergelijking los je op door termen van de ene naar de andere kant te brengen. Dus x-en links en de getallen rechts. Deel uiteindelijk beide leden door het getal voor de x. Zo vind je de oplossing. Ter controle vul de oplossing in en kijk of het klopt.
b. 7x - 6x = 8 - 3 geeft x = 5
c. -4x = 10 geeft x = -2½
d. 7x = -14 geeft x = -2
34.
a. -7x = 0 geeft x = 0
b. -y + 2y = 5 + 1 geeft y = 6
c. 8x = -16 geeft x = -2
d. -3a = -13 geeft a = 4⅓
35.
Tip:
Neem: -p = -8, deel links en rechts door -1 en dan krijg je: p = 8
a. 5x = -30 geeft x = -6Neem: -p = -8, deel links en rechts door -1 en dan krijg je: p = 8
b. 3p - 4p = -9 + 1 geeft -p = -8 dus p = 8
c. 3q - 8q + 3q = -2 + 2 geeft -2q = 0 dus q = 0
d. 5a - 4a + 2a = 6 geeft 3a = 6 dus a = 2
36.
Tip:
Bedenk: 4 x 21 = 4⋅(20 + 1) = 80 + 4 = 84
a. 5(3x - 7) = 15x - 35Bedenk: 4 x 21 = 4⋅(20 + 1) = 80 + 4 = 84
b. -2(6 - x) = -12 + 2x
c. -(x - 8) = -x + 8
d. -¼(3x + 12) = -¾x - 3
37.
Tip:
a. 5(x - 3) = 2x + 9 <=> 5x - 15 = 2x + 9 <=> 3x = 24 <=> x = 8
Vul de oplossing x = 8 in en je ziet: 5(8 - 3) = 2⋅8 + 9 <=> 5⋅5 = 16 + 9 <=> 25 = 25
Ja, het klopt! Dus we hebben de juiste x gevonden.
a. 3x = 24 levert x = 8a. 5(x - 3) = 2x + 9 <=> 5x - 15 = 2x + 9 <=> 3x = 24 <=> x = 8
Vul de oplossing x = 8 in en je ziet: 5(8 - 3) = 2⋅8 + 9 <=> 5⋅5 = 16 + 9 <=> 25 = 25
Ja, het klopt! Dus we hebben de juiste x gevonden.
b. 3p = 21 levert p = 7
c. 4x = 15 levert x = 3 3/4
d. -x = -10 levert x = 10
38.
a. 7x - 6x = -6 - 3 levert x = -9
b. 4x - 5x = -5 + 16 levert x = -11
c. -2x = -30 levert x = 15
d. 3x - 5x = 3 - 3 levert x = 0
39.
b. -p = 19 levert p = -19
c. 15k - 35 + 7 = 14k - 28 levert k = 0
d. 4x = 20 levert x = 5
40.
b. x = 6
41.
b. Doe eerst keer 10, dan volgt dat x = 20
c. Doe eerst keer 6, dan volgt dat x = 12
d. Doe eerst keer 12, dan volgt dat x = 3 3/5
42.
b. Eerst keer 10, 2x - 5 = 30 - 5x levert x = 5
c. Eerst haakjes wegwerken en dan keer 6, 3x + 3 = 2x + 4 levert x = 1
d. Eerst haakjes wegwerken en dan keer 12, 9x + 6 = 4x - 8 + 24 levert x = 2
e. Eerst haakjes wegwerken, -4t = -14 levert t = 3½
f. Eerst haakjes wegwerken, 2,1x = -2,1 levert x = -1
43.
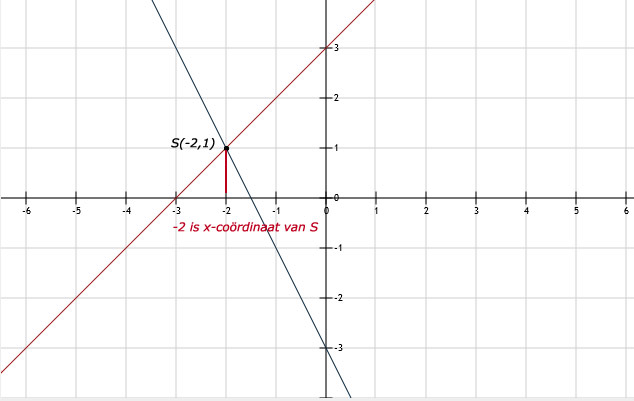
b. Coördinaten van het snijpunt S is (-2,1).
c. x + 3 = -2x - 3 <=> 3x = -6 <=> x = -2
d. De oplossing van de vergelijking is de x-coördinaat van het snijpunt S.
44.
1,8x = 4,5
x = 2,5 (x-coördinaat S)
y = 1,1 Dus coördinaten snijpunt S: (2,5 ; 1,1)
45.
a. 0,5x + 100 = 0,25x + 150
0,5x - 0,25x = 150 - 100
0,25x = 50
x = 200
Dus bij 200 km zijn de prijzen gelijk.
b. Neem hiervoor het snijpunt. Na 200 km is Vanhire goedkoper.
46.
a. De vergelijking die je dan moet oplossen is 65 + 12t = 50 + 15t
65 + 12t = 50 + 15t
12t - 15t = 50 - 65
-3t = -15
t = 5
Bedrijven zijn dus even duur bij 5 kwartier.
b. De reparatietijd is dan meer dan 5 kwartier.
47.
a. Los op: -1,5x + 5 = 1,5x - 4, levert x = 3 en y = 0,5. Snijpunt is dus: (3 ; 0,5)
b. Los op: -1,5x + 5 = 0,5x + 1, levert x = 2 en y = 2. Snijpunt is dus: (2,2)
Tip:
Werkschema om een lineaire vergelijking op te lossen:
- Haakjes wegwerken
- Alle x-en naar links, getallen naar rechts
- Herleid beide leden (alles bij elkaar vegen)
- Deel links en rechts door het getal voor de x
- Controleer je oplossing
a. 6a = 18 levert a = 3Werkschema om een lineaire vergelijking op te lossen:
- Haakjes wegwerken
- Alle x-en naar links, getallen naar rechts
- Herleid beide leden (alles bij elkaar vegen)
- Deel links en rechts door het getal voor de x
- Controleer je oplossing
b. -p = 19 levert p = -19
c. 15k - 35 + 7 = 14k - 28 levert k = 0
d. 4x = 20 levert x = 5
40.
Tip:
4 - 3(x - 7) = 4 - 3x + 21 = 25 - 3x
-3 keer x is -3x en
-3 x -7 is +21
a. x = -254 - 3(x - 7) = 4 - 3x + 21 = 25 - 3x
-3 keer x is -3x en
-3 x -7 is +21
b. x = 6
41.
Tip:
Om breuken weg te werken, vermenigvuldig links en rechts met hetzelfde getal.
a. Doe eerst keer 4, dan volgt dat x = -16Om breuken weg te werken, vermenigvuldig links en rechts met hetzelfde getal.
b. Doe eerst keer 10, dan volgt dat x = 20
c. Doe eerst keer 6, dan volgt dat x = 12
d. Doe eerst keer 12, dan volgt dat x = 3 3/5
42.
Tip:
Werk eventueel eerst de haakjes weg en daarna de breuken.
a. Eerst keer 12, 3x + 12 = -36 + 4x levert x = 48Werk eventueel eerst de haakjes weg en daarna de breuken.
b. Eerst keer 10, 2x - 5 = 30 - 5x levert x = 5
c. Eerst haakjes wegwerken en dan keer 6, 3x + 3 = 2x + 4 levert x = 1
d. Eerst haakjes wegwerken en dan keer 12, 9x + 6 = 4x - 8 + 24 levert x = 2
e. Eerst haakjes wegwerken, -4t = -14 levert t = 3½
f. Eerst haakjes wegwerken, 2,1x = -2,1 levert x = -1
43.
Tip:
y = ax + b, snijpunt met de y-as is (0,b)
a. Bij l: hoort y = x + 3y = ax + b, snijpunt met de y-as is (0,b)
b. Coördinaten van het snijpunt S is (-2,1).
c. x + 3 = -2x - 3 <=> 3x = -6 <=> x = -2
d. De oplossing van de vergelijking is de x-coördinaat van het snijpunt S.

44.
Tip:
Stel de vergelijkingen gelijk aan elkaar f(x) = g(x) en los de vergelijking op. De uitkomst levert de x-coördinaat van het snijpunt S. Vul deze x-coördinaat in 1 van de formules en je krijgt de y-coördinaat van S.
Stel: 0,6x - 0,4 = -1,2x + 4,1Stel de vergelijkingen gelijk aan elkaar f(x) = g(x) en los de vergelijking op. De uitkomst levert de x-coördinaat van het snijpunt S. Vul deze x-coördinaat in 1 van de formules en je krijgt de y-coördinaat van S.
1,8x = 4,5
x = 2,5 (x-coördinaat S)
y = 1,1 Dus coördinaten snijpunt S: (2,5 ; 1,1)
45.
a. 0,5x + 100 = 0,25x + 150
0,5x - 0,25x = 150 - 100
0,25x = 50
x = 200
Dus bij 200 km zijn de prijzen gelijk.
b. Neem hiervoor het snijpunt. Na 200 km is Vanhire goedkoper.
46.
a. De vergelijking die je dan moet oplossen is 65 + 12t = 50 + 15t
65 + 12t = 50 + 15t
12t - 15t = 50 - 65
-3t = -15
t = 5
Bedrijven zijn dus even duur bij 5 kwartier.
b. De reparatietijd is dan meer dan 5 kwartier.
47.
a. Los op: -1,5x + 5 = 1,5x - 4, levert x = 3 en y = 0,5. Snijpunt is dus: (3 ; 0,5)
b. Los op: -1,5x + 5 = 0,5x + 1, levert x = 2 en y = 2. Snijpunt is dus: (2,2)
Andere paragrafen:
1.1. Lineaire formules (1 t/m 12)
1.2. Lineaire formules opstellen (13 t/m 28)
1.3. Lineaire vergelijkingen (29 t/m 47)
1.4. Lineaire functies (48 t/m 57)
1.5. Snijpunten van grafieken (58 t/m 68)
1.1. Lineaire formules (1 t/m 12)
1.2. Lineaire formules opstellen (13 t/m 28)
1.3. Lineaire vergelijkingen (29 t/m 47)
1.4. Lineaire functies (48 t/m 57)
1.5. Snijpunten van grafieken (58 t/m 68)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


