TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 6.1 Parabolen HAVO 3
Boek: Getal & Ruimte - Vergelijkingen en parabolen HAVO 3 (deel 2) opgaven 1 t/m 9, 2010Basisformule van een parabool is: ax2 + bx + c, met a ≠ 0.
Om de snijpunten van een parabool met de x-as te berekenen, lossen we op f(x) = 0.
Om het snijpunt van een parabool met de y-as te berekenen, lossen we op f(0).
Om de snijpunten met de x-as te bepalen (f(x) = 0 oplossen) maken we o.a. gebruik van: ontbinden in factoren en de product-som-methode. Bij ontbinden in factoren nemen we een gemeenschappelijke factor voor de haakjes. Bij de product-som-methode maak je een T-tabel.
Het berekenen van het snijpunt met de y-as f(0) is vaak heel gemakkelijk.
Om de snijpunten van een parabool met de x-as te berekenen, lossen we op f(x) = 0.
Om het snijpunt van een parabool met de y-as te berekenen, lossen we op f(0).
Om de snijpunten met de x-as te bepalen (f(x) = 0 oplossen) maken we o.a. gebruik van: ontbinden in factoren en de product-som-methode. Bij ontbinden in factoren nemen we een gemeenschappelijke factor voor de haakjes. Bij de product-som-methode maak je een T-tabel.
Het berekenen van het snijpunt met de y-as f(0) is vaak heel gemakkelijk.
1.
b. Y(b) = 4
c. Snijpunt met de y-as (in punt B), dan is dus xB = 0.
yB = -4. Dus snijpunt met de y-as is (0,-4).
2.
yA = h(4) = 30
yB = h(-5) = 102
b.
h(-1) = 3 + 5 + 2 = 10, dus (-1,10) ligt inderdaad op de grafiek h.
3.
yA = f(-2) = -4
yB = f(0) = 5
yC = f(2) = 6
b. f(-1) = 1,5 dus P(-1,3 1/2) ligt NIET op de grafiek van f.
4.
b. (x+2)(x-7)
c. (x+3)(x+6)
d. x(3x-8)
e. (x+8)(x-9)
f. (x+3)(x-4)
g. (x+1)(x+5)
h. (x+2)(x+3)
5.
b. f(1) = 1 - 6 + 5 = 0 en f(5) = 25 - 30 + 5 = 0. Dus de punten A en B zijn A(1,0) en B(5,0).
6.
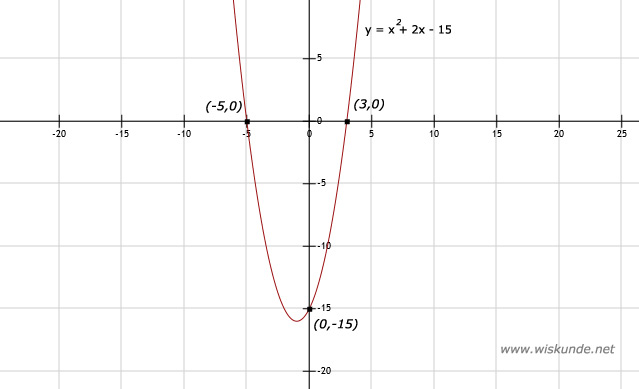
Los op: f(x) = 0
x2 + 2x - 15 = 0
(x + 5)(x - 3) = 0
x + 5 = 0 v x - 3 = 0
x = -5 v x = 3
Snijpunten met x-as zijn A(-5,0) en B(3,0).
Snijpunt met y-as:
Los op: f(0) = ?
f(0) = 02 + 2⋅0 - 15 = -15
Snijpunt met de y-as is C(0,-15).
7.
a. x = 3 of x = 4
b. x = 0 of x = 1
c. x = -1
d. x = 0 of x = 4
e. x = -2 of x = 3
f. x = -1 of x = 6
8.
b. x = 0 of x = 4
c. x = -5 of x = 9
d. x = 1 of x = 10
e. x = 0 of x = 1/4
f. x = 1 of x = 2
9.
b. Snijpunt met de x-as is (-3,0)
c. Snijpunten met de x-as zijn (3,0) en (4,0)
d. Snijpunten met de x-as zijn (-12,0) en (2,0)
Tip:
Bij een parabool y = ax2 + bx + c:
Als a < 0 dan is het een bergparabool
Als a > 0 dan is het een dalparabool
a. Dat kun je zien je aan de - voor de x2Bij een parabool y = ax2 + bx + c:
Als a < 0 dan is het een bergparabool
Als a > 0 dan is het een dalparabool
b. Y(b) = 4
c. Snijpunt met de y-as (in punt B), dan is dus xB = 0.
yB = -4. Dus snijpunt met de y-as is (0,-4).
2.
Tip:
Bij b: vul het punt P(-1,10) in in de functie van h(x).
a. Bij b: vul het punt P(-1,10) in in de functie van h(x).
yA = h(4) = 30
yB = h(-5) = 102
b.
h(-1) = 3 + 5 + 2 = 10, dus (-1,10) ligt inderdaad op de grafiek h.
3.
Tip:
Stel de coördinaten van punt A zijn: A(-2,-4).
xA is de x-coördinaat van het punt A. Dus -2.
yA is de y-coördinaat van het punt A. Dus -4.
a. Stel de coördinaten van punt A zijn: A(-2,-4).
xA is de x-coördinaat van het punt A. Dus -2.
yA is de y-coördinaat van het punt A. Dus -4.
yA = f(-2) = -4
yB = f(0) = 5
yC = f(2) = 6
b. f(-1) = 1,5 dus P(-1,3 1/2) ligt NIET op de grafiek van f.
4.
Tip:
Probeer eerst een zo groot mogelijke gemeenschappelijke factor voor de haakjes te brengen.
Lukt dat niet? Gebruik dan de product-som-methode.
a. 3x(x+4)Probeer eerst een zo groot mogelijke gemeenschappelijke factor voor de haakjes te brengen.
Lukt dat niet? Gebruik dan de product-som-methode.
b. (x+2)(x-7)
c. (x+3)(x+6)
d. x(3x-8)
e. (x+8)(x-9)
f. (x+3)(x-4)
g. (x+1)(x+5)
h. (x+2)(x+3)
5.
Tip:
Snijpunten (x,y) met de x-as, dan y = 0. Voorbeelden hiervan zijn: (-6,0) en (10,0).
Snijpunt (x,y) met de y-as, dan x = 0. Voorbeelden hiervan zijn: (0,-3) en (0,7).
a. f(0) = 0 - 0 + 5 = 5, dus je weet nu dat C is (0,5).Snijpunten (x,y) met de x-as, dan y = 0. Voorbeelden hiervan zijn: (-6,0) en (10,0).
Snijpunt (x,y) met de y-as, dan x = 0. Voorbeelden hiervan zijn: (0,-3) en (0,7).
b. f(1) = 1 - 6 + 5 = 0 en f(5) = 25 - 30 + 5 = 0. Dus de punten A en B zijn A(1,0) en B(5,0).
6.
Tip:
Snijpunt(en) x-as: f(x) = 0 oplossen
Snijpunt y-as: f(0) oplossen
Snijpunten met x-as:Snijpunt(en) x-as: f(x) = 0 oplossen
Snijpunt y-as: f(0) oplossen
Los op: f(x) = 0
x2 + 2x - 15 = 0
(x + 5)(x - 3) = 0
x + 5 = 0 v x - 3 = 0
x = -5 v x = 3
Snijpunten met x-as zijn A(-5,0) en B(3,0).
Snijpunt met y-as:
Los op: f(0) = ?
f(0) = 02 + 2⋅0 - 15 = -15
Snijpunt met de y-as is C(0,-15).

7.
a. x = 3 of x = 4
b. x = 0 of x = 1
c. x = -1
d. x = 0 of x = 4
e. x = -2 of x = 3
f. x = -1 of x = 6
8.
Tip:
Maak eerst het rechterlid '... = 0'.
Dit doe je met de balansmethode.
a. x = 3 of x = -4Maak eerst het rechterlid '... = 0'.
Dit doe je met de balansmethode.
b. x = 0 of x = 4
c. x = -5 of x = 9
d. x = 1 of x = 10
e. x = 0 of x = 1/4
f. x = 1 of x = 2
9.
Tip:
Snijpunten met de x-as dan y = 0 ofwel f(x) = 0 en los op.
a. Snijpunten met de x-as zijn (0,0) en (2,0)Snijpunten met de x-as dan y = 0 ofwel f(x) = 0 en los op.
b. Snijpunt met de x-as is (-3,0)
c. Snijpunten met de x-as zijn (3,0) en (4,0)
d. Snijpunten met de x-as zijn (-12,0) en (2,0)
Andere paragrafen:
6.1. Parabolen (1 t/m 9)
6.2. De abc-formule (10 t/m 25)
6.3. De ligging van een parabool ten opzichte van de x-as (26 t/m 31)
6.4. Kwadratische vergelijkingen toepassen (32 t/m 38)
6.5. Grafieken veranderen (39 t/m 53)
6.1. Parabolen (1 t/m 9)
6.2. De abc-formule (10 t/m 25)
6.3. De ligging van een parabool ten opzichte van de x-as (26 t/m 31)
6.4. Kwadratische vergelijkingen toepassen (32 t/m 38)
6.5. Grafieken veranderen (39 t/m 53)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


