TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 6.5 Grafieken veranderen HAVO 3
Boek: Getal & Ruimte - Vergelijkingen en parabolen HAVO 3 (deel 2) opgaven 39 t/m 53, 2010Parabolen kunnen zowel horizontaal als verticaal verschuiven.
Neem als basisgrafiek y = x2
Verticaal verschuiven:
Als deze 3 omhoog gaat, dan wordt de formule: y = x2 + 3
Als deze 4 omlaag gaat, dan wordt de formule: y = x2 - 4
Horizontaal verschuiven:
Als deze 3 naar links gaat, dan wordt de formule: y = (x + 3)2 (vervang x door x + 3)
Als deze 4 naar rechts gaat, dan wordt de formule: y = (x - 4)2 (vervang x door x - 4)
Neem als basisgrafiek y = x2
Verticaal verschuiven:
Als deze 3 omhoog gaat, dan wordt de formule: y = x2 + 3
Als deze 4 omlaag gaat, dan wordt de formule: y = x2 - 4
Horizontaal verschuiven:
Als deze 3 naar links gaat, dan wordt de formule: y = (x + 3)2 (vervang x door x + 3)
Als deze 4 naar rechts gaat, dan wordt de formule: y = (x - 4)2 (vervang x door x - 4)
39.
b. Schuif de rode grafiek 1 omlaag
40.
Parabool a: y = x2 + 1
Parabool b: y = x2 - 1
Parabool c: y = x2 - 2
b.
Parabool d: y = -0,2x2 + 2
Parabool e: y = -0,2x2 + 1
Parabool f: y = -0,2x2 - 1
41.
b. k(x) = 1/3x2 - 4
42.
Plaatje II hoort bij f(x)
Plaatje III hoort bij k(x)
Plaatje IV hoort bij g(x)
43.
b. Dalparabool met Top door (0,0) en dus 1 snijpunt met de x-as
c. Dalparabool met Top boven (0,0) en 0 snijpunten met de x-as
d. Bergparabool met Top door (0,0) en dus 1 snijpunt met de x-as
e. Dalparabool met Top onder (0,0) en 2 snijpunten met de x-as
f. Bergparabool met Top boven (0,0) en 2 snijpunten met de x-as
g. Dalparabool met Top boven (0,0) en 0 snijpunten met de x-as
h. Bergparabool met Top onder (0,0) en 0 snijpunten met de x-as
44.
a.
b. g(18) = 256, dus voor x = 18.
c. g(27) = 625, dus voor x = 27.
45.
b. y = -1/4(x + 5)2
46.
b. y = -(x - 4)2 + 2
c. y = -(x + 7)2 + 6
d. y = -(x + 2)2 - 1
47.
a. 2 naar rechts en 5 omhoog
b. 1 naar links en 4 omlaag
c. 4 naar rechts en 2 omlaag
48.
b. De top van h(x): (0,5)
c. De top van k(x): (3,-1)
Tip:
Je schuift hier dus over een verticale as.
a. Schuif de rode grafiek 2 omhoogJe schuift hier dus over een verticale as.
b. Schuif de rode grafiek 1 omlaag
40.
Tip:
Je begint met y = x2 + a. Bepaal steeds de waarde van 'a'.
a. Je begint met y = x2 + a. Bepaal steeds de waarde van 'a'.
Parabool a: y = x2 + 1
Parabool b: y = x2 - 1
Parabool c: y = x2 - 2
b.
Parabool d: y = -0,2x2 + 2
Parabool e: y = -0,2x2 + 1
Parabool f: y = -0,2x2 - 1
41.
Tip:
Haakjesnotatie van g: g(x)
a. g(x) = -2x2 + 6Haakjesnotatie van g: g(x)
b. k(x) = 1/3x2 - 4
42.
Tip:
Vul x = 0 in en je krijgt het snijpunt met de y-as. Het getal voor de x2 bepaalt of het een berg- of dalparabool is.
Plaatje I hoort bij h(x)Vul x = 0 in en je krijgt het snijpunt met de y-as. Het getal voor de x2 bepaalt of het een berg- of dalparabool is.
Plaatje II hoort bij f(x)
Plaatje III hoort bij k(x)
Plaatje IV hoort bij g(x)
43.
Tip:
Neem als basis y = x2. Bekijk wat de verticale verschuiving is. Bepaal daarna of het een berg- of dalparabool is.
a. Dalparabool met Top onder (0,0) en 2 snijpunten met de x-asNeem als basis y = x2. Bekijk wat de verticale verschuiving is. Bepaal daarna of het een berg- of dalparabool is.
b. Dalparabool met Top door (0,0) en dus 1 snijpunt met de x-as
c. Dalparabool met Top boven (0,0) en 0 snijpunten met de x-as
d. Bergparabool met Top door (0,0) en dus 1 snijpunt met de x-as
e. Dalparabool met Top onder (0,0) en 2 snijpunten met de x-as
f. Bergparabool met Top boven (0,0) en 2 snijpunten met de x-as
g. Dalparabool met Top boven (0,0) en 0 snijpunten met de x-as
h. Bergparabool met Top onder (0,0) en 0 snijpunten met de x-as
44.
a.
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| f(x) | 0 | 1 | 4 | 9 | 16 | 25 |
| x | 2 | 3 | 4 | 5 | 6 | 7 |
| g(x) | 0 | 1 | 4 | 9 | 16 | 25 |
c. g(27) = 625, dus voor x = 27.
45.
Tip:
3 naar rechts, vervang x door (x - 3)
5 naar links, vervang x door (x + 5)
a. y = 4/5(x - 3)2 + 23 naar rechts, vervang x door (x - 3)
5 naar links, vervang x door (x + 5)
b. y = -1/4(x + 5)2
46.
Tip:
Omlaag of omhoog? Dan verandert de +2 in de formule.
Links of rechts? Dan verandert de x in de formule.
a. y = -x2 - 1Omlaag of omhoog? Dan verandert de +2 in de formule.
Links of rechts? Dan verandert de x in de formule.
b. y = -(x - 4)2 + 2
c. y = -(x + 7)2 + 6
d. y = -(x + 2)2 - 1
47.
a. 2 naar rechts en 5 omhoog
b. 1 naar links en 4 omlaag
c. 4 naar rechts en 2 omlaag
48.
Tip:
Om te bepalen wat de verschuiving is, kijk je naar de toppen van de parabolen.
a. Door f(x) 3 omlaag te verschuiven, ontstaat g(x). De top van g(x) wordt dan (0,-3).Om te bepalen wat de verschuiving is, kijk je naar de toppen van de parabolen.
b. De top van h(x): (0,5)
c. De top van k(x): (3,-1)
49.
b. De top is (-2,7) en a=-3 dus het is een bergparabool
c. De top is (2,-3) en a=7 dus het is een dalparabool
d. De top is (7,3) en a=-2 dus het is een bergparabool
50.
b. De top is (0,-3) en a=1 dus het is een dalparabool
c. De top is (3,0) en a=1 dus het is een dalparabool
d. De top is (-3,-5) en a=-1 dus het is een bergparabool
e. De top is (0,5) en a=-3 dus het is een bergparabool
f. De top is (-5,0) en a=-3 dus het is een bergparabool
51.
a. 4 graden
b. Om 18:00 en om 17:10
c. Tussen 08:00 en 17:00
d. *
52.
*
53.
a. y = 3x2 + 30
b. y = 0,05(x + 3)2
c. y = 2(x - 1)2
d. y = -0,5x2 - 6
Tip:
Top van een parabool van de vorm: y = a(x - p)2 + q is (p,q).
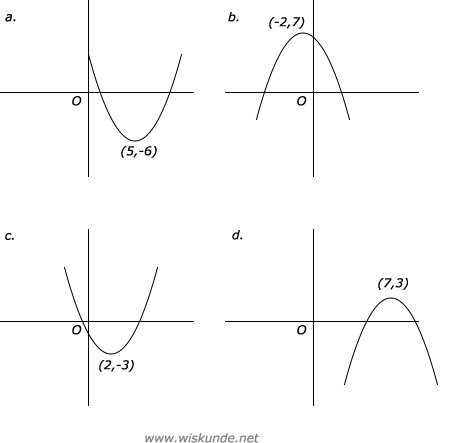
a. De top is (5,-6) en a=1 dus het is een dalparaboolTop van een parabool van de vorm: y = a(x - p)2 + q is (p,q).
b. De top is (-2,7) en a=-3 dus het is een bergparabool
c. De top is (2,-3) en a=7 dus het is een dalparabool
d. De top is (7,3) en a=-2 dus het is een bergparabool

50.
Tip:
Bij y = a(x - p)2 + q bepaalt de 'a' of het een berg- of dalparabool is.
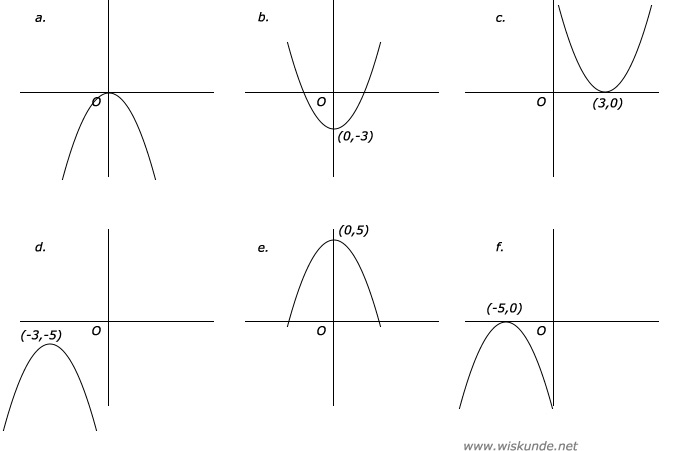
a. De top is (0,0) en a=-3 dus het is een bergparaboolBij y = a(x - p)2 + q bepaalt de 'a' of het een berg- of dalparabool is.
b. De top is (0,-3) en a=1 dus het is een dalparabool
c. De top is (3,0) en a=1 dus het is een dalparabool
d. De top is (-3,-5) en a=-1 dus het is een bergparabool
e. De top is (0,5) en a=-3 dus het is een bergparabool
f. De top is (-5,0) en a=-3 dus het is een bergparabool

51.
a. 4 graden
b. Om 18:00 en om 17:10
c. Tussen 08:00 en 17:00
d. *
52.
*
53.
a. y = 3x2 + 30
b. y = 0,05(x + 3)2
c. y = 2(x - 1)2
d. y = -0,5x2 - 6
Andere paragrafen:
6.1. Parabolen (1 t/m 9)
6.2. De abc-formule (10 t/m 25)
6.3. De ligging van een parabool ten opzichte van de x-as (26 t/m 31)
6.4. Kwadratische vergelijkingen toepassen (32 t/m 38)
6.5. Grafieken veranderen (39 t/m 53)
6.1. Parabolen (1 t/m 9)
6.2. De abc-formule (10 t/m 25)
6.3. De ligging van een parabool ten opzichte van de x-as (26 t/m 31)
6.4. Kwadratische vergelijkingen toepassen (32 t/m 38)
6.5. Grafieken veranderen (39 t/m 53)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


