TIP: Wil je ook toegang tot meer dan 17.100 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 7.2 Goniometrische verhoudingen HAVO 3
Boek: Getal & Ruimte - Goniometrie HAVO 3 (deel 2) opgaven 13 t/m 32, 2010SOS CAS TOA - Goniometrische verhoudingen
sin(∠A) (SOS) = overstaande rechthoekszijde van die ∠A / schuine zijde
cos(∠A) (CAS) = aanliggende rechthoekszijde van die ∠A / schuine zijde
tan(∠A) (TOA) = overstaande rechthoekszijde van die ∠A / aanliggende rechthoekszijde van die ∠A
sin(∠A) (SOS) = overstaande rechthoekszijde van die ∠A / schuine zijde
cos(∠A) (CAS) = aanliggende rechthoekszijde van die ∠A / schuine zijde
tan(∠A) (TOA) = overstaande rechthoekszijde van die ∠A / aanliggende rechthoekszijde van die ∠A
13.
a. sin(∠A) = 3/5 dus ∠A = sin-1(3/5) ≈ 36,9º
b. Verhouding AB / AC = 0,8 en cos(36,9) ≈ 0,8
14.
a. cos(∠A) = AB / AC
b. sin(∠C) = AB / AC
c. tan(∠A) = BC / AB
d. cos(∠C) = BC / AC
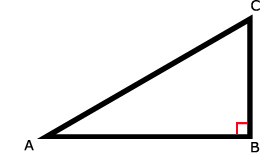
15.
a. sin(∠C) = AD / AC
b. cos(∠B) = BD / AB
c. tan(∠A1) = BD / AD
d. sin(∠A2) = CD / AC
e. cos(∠C) = CD / AC
f. tan(∠B) = AD / BD
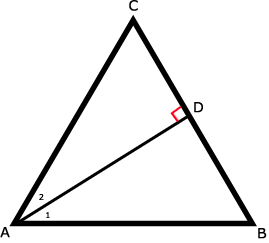
16.
a. tan(∠A) = CD / AD
b. sin(∠B) = CD / BC
c. cos(∠C1) = CD / AC
d. sin(∠C2) = BD / BC
17.
a. ∠A = cos-1(0,81) ≈ 35,9º
b. ∠A = sin-1(0,81) ≈ 54,1º
c. ∠A = tan-1(0,81) ≈ 39,0º
d. ∠A = cos-1(0,08) ≈ 85,4º
e. ∠A = sin-1(0,02) ≈ 1,1º
f. ∠A = cos-1(0,98) ≈ 11,5º
18.
a. BC is de aanliggende rechthoekszijde van ∠B. AB is de schuine zijde van driehoek ABC.
b.cos(∠B) = BC / AB = 7/9, dus ∠B = cos-1(7/9) ≈ 38,9º
19.
a. cos(∠A) = AC / AB = 4/7, dus ∠A = cos-1(4/7) ≈ 55,2º
b. sin(∠E) = DF / DE = 5/12,5, dus ∠E = sin-1(5/12,5) ≈ 23,6º
c. tan(∠M) = KL / KM = 3/6, dus ∠M = tan-1(3/6) ≈ 26,6º
20.
b. tan(∠F1) = DG / FG = 2/5, dus ∠F1 = tan-1(2/5) ≈ 21,8º
cos(∠F2) = FG / EF = 5/9, dus ∠F2 = cos-1(5/9) ≈ 56,3º
c. tan(∠L1) = KM / KL = 6/3, dus ∠L1 = tan-1(6/3) ≈ 63,4º
sin(∠N) = KL / LN = 3/4, dus ∠N = sin-1(3/4) ≈ 48,6º
21.
a. Je moet de sin van ∠B gebruiken om de zijde AC te kunnen berekenen.
b. AC = 7 x sin(29º) ≈ 3,39
22.
a. sin(∠D) = EF / DE, hieruit volgt EF = 4,2 x sin(56º) ≈ 3,48
b. Met de stelling van Pythagoras DF = √5,5296 ≈ 2,35
Met cos(∠D) = DF / DE, hieruit volgt DF = 4,2 x cos(56º) ≈ 2,35
c. De cosinus manier is sneller.
a. sin(∠A) = 3/5 dus ∠A = sin-1(3/5) ≈ 36,9º
b. Verhouding AB / AC = 0,8 en cos(36,9) ≈ 0,8
14.
a. cos(∠A) = AB / AC
b. sin(∠C) = AB / AC
c. tan(∠A) = BC / AB
d. cos(∠C) = BC / AC

15.
a. sin(∠C) = AD / AC
b. cos(∠B) = BD / AB
c. tan(∠A1) = BD / AD
d. sin(∠A2) = CD / AC
e. cos(∠C) = CD / AC
f. tan(∠B) = AD / BD

16.
a. tan(∠A) = CD / AD
b. sin(∠B) = CD / BC
c. cos(∠C1) = CD / AC
d. sin(∠C2) = BD / BC
17.
a. ∠A = cos-1(0,81) ≈ 35,9º
b. ∠A = sin-1(0,81) ≈ 54,1º
c. ∠A = tan-1(0,81) ≈ 39,0º
d. ∠A = cos-1(0,08) ≈ 85,4º
e. ∠A = sin-1(0,02) ≈ 1,1º
f. ∠A = cos-1(0,98) ≈ 11,5º
18.
a. BC is de aanliggende rechthoekszijde van ∠B. AB is de schuine zijde van driehoek ABC.
b.cos(∠B) = BC / AB = 7/9, dus ∠B = cos-1(7/9) ≈ 38,9º
19.
a. cos(∠A) = AC / AB = 4/7, dus ∠A = cos-1(4/7) ≈ 55,2º
b. sin(∠E) = DF / DE = 5/12,5, dus ∠E = sin-1(5/12,5) ≈ 23,6º
c. tan(∠M) = KL / KM = 3/6, dus ∠M = tan-1(3/6) ≈ 26,6º
20.
Tip:
Bekijk eerst of je sin, cos of tan gaat gebruiken.
a. cos(∠A) = AB / AC = 4/5, dus ∠A = cos-1(4/5) ≈ 36,9ºBekijk eerst of je sin, cos of tan gaat gebruiken.
b. tan(∠F1) = DG / FG = 2/5, dus ∠F1 = tan-1(2/5) ≈ 21,8º
cos(∠F2) = FG / EF = 5/9, dus ∠F2 = cos-1(5/9) ≈ 56,3º
c. tan(∠L1) = KM / KL = 6/3, dus ∠L1 = tan-1(6/3) ≈ 63,4º
sin(∠N) = KL / LN = 3/4, dus ∠N = sin-1(3/4) ≈ 48,6º
21.
a. Je moet de sin van ∠B gebruiken om de zijde AC te kunnen berekenen.
b. AC = 7 x sin(29º) ≈ 3,39
22.
a. sin(∠D) = EF / DE, hieruit volgt EF = 4,2 x sin(56º) ≈ 3,48
b. Met de stelling van Pythagoras DF = √5,5296 ≈ 2,35
Met cos(∠D) = DF / DE, hieruit volgt DF = 4,2 x cos(56º) ≈ 2,35
c. De cosinus manier is sneller.
23.
a. sin(∠B) = AC / BC, hieruit volgt BC = ( 1 x 5 ) / sin(26º) ≈ 11,41
b. tan(∠P) = QR / PR, hieruit volgt QR = 8 x tan(35º) ≈ 5,60
c. cos(∠M) = LM / KM, hieruit volgt LM = 13 x cos(56º) ≈ 7,27
24.
25.
26.
∠Q = 180º - 90º - 31,8º = 58,2º
27.
a. cos(∠A) = AD / AC = 2/6, neem dan de cos-1 en je krijgt ∠A = cos-1(2/6) ≈ 70,5º.
b. Je rekent met een afgerond getal. Dus je krijgt afrondingsverschillen waardoor het minder nauwkeurig is.
c. ∠C = 180º - 2 x cos-1(2/6) ≈ 38,94º
28.
Teken de loodlijn PS.
a. cos(∠Q) = QS / PQ = 2,35 / 6,8
∠Q = cos-1(2,35 / 6,8) ≈ 69,8º
∠Q = ∠R = 69,8º omdat het een gelijkbenige driehoek is (gelijke basishoeken)
∠P = 180 - 2 x 69,8º = 40,4º
29.
∠B1 = ∠B2 = 70º/2 = 35º
sin(∠B1) = AD / AB
AD = 6 x sin(35º) ≈ 3,441458
Hieruit volgt dat AC = 2 x AD ≈ 6,88
30.
Hoogte dak = 6,5 x sin(57º) ≈ 5,5 meter. Dus de nok zit op 2,8 + 5,5 = 8,3 meter.
31.
AB= (1 x 5) / tan(28º) ≈ 9,40
AD = 5 x cos(28º) ≈ 4,41
CD = 5 x sin(28º) ≈ 2,35
32.
tan(∠B) = CD / BC, hieruit volgt dat BC = 5,55
AC = AB + BC = 8 + 5,55 = 13,55
In driehoek ACD zie je tan(∠A) = CD / AC = 5 / 13,55 dus ∠A = tan-1(5 / 13,55) ≈ 20,3º
a. sin(∠B) = AC / BC, hieruit volgt BC = ( 1 x 5 ) / sin(26º) ≈ 11,41
b. tan(∠P) = QR / PR, hieruit volgt QR = 8 x tan(35º) ≈ 5,60
c. cos(∠M) = LM / KM, hieruit volgt LM = 13 x cos(56º) ≈ 7,27
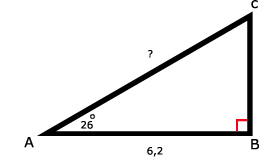
24.
Tip:
Je gebruikt de aanliggende rechthoekszijde (A) en de schuine zijde (S) van ∠A. Gebruik dus de cos.
cos(∠A) = AB / AC, hieruit volgt AC = ( 1 x 6,2 ) / cos(26º) ≈ 6,90Je gebruikt de aanliggende rechthoekszijde (A) en de schuine zijde (S) van ∠A. Gebruik dus de cos.

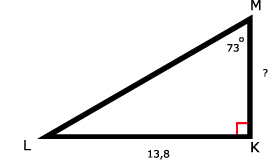
25.
Tip:
Je gebruikt de overstaande rechthoekszijde (O) en de aanliggende rechthoekszijde (A) van ∠M. Gebruik dus de tan.
tan(∠M) = KL / KM, hieruit volgt KM = ( 1 x 13,8 ) / tan(73º) ≈ 4,22Je gebruikt de overstaande rechthoekszijde (O) en de aanliggende rechthoekszijde (A) van ∠M. Gebruik dus de tan.

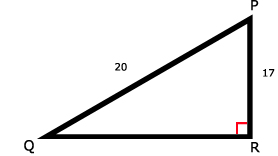
26.
Tip:
Het kan zijn dat jouw schets er iets anders uitziet dan mijn schets. Zolang je alles maar goed neerzet in de driehoek.
Bereken eerst ∠P en bereken daarna ∠Q met de hoekensom (180º).
cos(∠P) = PR / PQ = 17 / 20, hieruit volgt ∠P ≈ 31,8º (via cos-1(17/20))Het kan zijn dat jouw schets er iets anders uitziet dan mijn schets. Zolang je alles maar goed neerzet in de driehoek.
Bereken eerst ∠P en bereken daarna ∠Q met de hoekensom (180º).
∠Q = 180º - 90º - 31,8º = 58,2º

27.
a. cos(∠A) = AD / AC = 2/6, neem dan de cos-1 en je krijgt ∠A = cos-1(2/6) ≈ 70,5º.
b. Je rekent met een afgerond getal. Dus je krijgt afrondingsverschillen waardoor het minder nauwkeurig is.
c. ∠C = 180º - 2 x cos-1(2/6) ≈ 38,94º
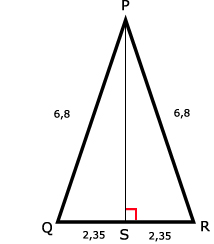
28.
Teken de loodlijn PS.
a. cos(∠Q) = QS / PQ = 2,35 / 6,8
∠Q = cos-1(2,35 / 6,8) ≈ 69,8º
∠Q = ∠R = 69,8º omdat het een gelijkbenige driehoek is (gelijke basishoeken)
∠P = 180 - 2 x 69,8º = 40,4º

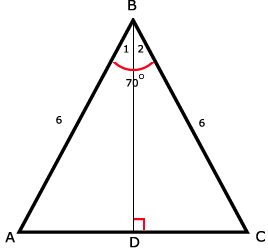
29.
∠B1 = ∠B2 = 70º/2 = 35º
sin(∠B1) = AD / AB
AD = 6 x sin(35º) ≈ 3,441458
Hieruit volgt dat AC = 2 x AD ≈ 6,88

30.
Hoogte dak = 6,5 x sin(57º) ≈ 5,5 meter. Dus de nok zit op 2,8 + 5,5 = 8,3 meter.
31.
AB= (1 x 5) / tan(28º) ≈ 9,40
AD = 5 x cos(28º) ≈ 4,41
CD = 5 x sin(28º) ≈ 2,35
32.
tan(∠B) = CD / BC, hieruit volgt dat BC = 5,55
AC = AB + BC = 8 + 5,55 = 13,55
In driehoek ACD zie je tan(∠A) = CD / AC = 5 / 13,55 dus ∠A = tan-1(5 / 13,55) ≈ 20,3º
Andere paragrafen:
7.1. Hellingen (1 t/m 12)
7.2. Goniometrische verhoudingen (13 t/m 32)
7.3. Berekeningen met sinus, cosinus & tangens (33 t/m 42)
7.4. Berekeningen in de ruimte (43 t/m 50)
7.5. Lijnstukken berekenen (51 t/m 56)
7.1. Hellingen (1 t/m 12)
7.2. Goniometrische verhoudingen (13 t/m 32)
7.3. Berekeningen met sinus, cosinus & tangens (33 t/m 42)
7.4. Berekeningen in de ruimte (43 t/m 50)
7.5. Lijnstukken berekenen (51 t/m 56)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


