TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 9.2 Hoeken berekenen met sinus, cosinus en tangens VMBO 3 KGT
Boek: Getal & Ruimte - Goniometrie 2 VMBO 3 (deel 2) opgaven 9 t/m 20, 2011SOS CAS TOA - Goniometrische verhoudingen
sin(∠A) (SOS) = overstaande rechthoekszijde van die ∠A / schuine zijde
cos(∠A) (CAS) = aanliggende rechthoekszijde van die ∠A / schuine zijde
tan(∠A) (TOA) = overstaande rechthoekszijde van die ∠A / aanliggende rechthoekszijde van die ∠A
De schuine zijde noemen we ook wel de hypotenusa.
sin(∠A) (SOS) = overstaande rechthoekszijde van die ∠A / schuine zijde
cos(∠A) (CAS) = aanliggende rechthoekszijde van die ∠A / schuine zijde
tan(∠A) (TOA) = overstaande rechthoekszijde van die ∠A / aanliggende rechthoekszijde van die ∠A
De schuine zijde noemen we ook wel de hypotenusa.
9.
Het woord dat je over houdt is "delen".
10.
a. sin ∠A = BC / AB
b. cos ∠A = AC / AB
c. tan ∠A = BC / AC
d. sin ∠B = AC / AB
e. cos ∠B = BC / AB
f. tan ∠B = AC / BC
11.
a. Schuine zijde
b. Overstaande rechthoekszijde van ∠D
c. Met de sinus kun je hoek D berekenen.
d. ∠D ≈ 62º
12.
a. Gebruik sin ∠L om de hoek te berekenen.
b. ∠L ≈ 55,4º
13.
14.
∠T ≈ 49º
15.
∠B ≈ 56,98º
∠C ≈ 12,15º
16.
∠K ≈ 41º
∠L ≈ 28º
∠M ≈ 23º
17.
18.
b. Ja, de ladder staat prima.
Het woord dat je over houdt is "delen".
10.
a. sin ∠A = BC / AB
b. cos ∠A = AC / AB
c. tan ∠A = BC / AC
d. sin ∠B = AC / AB
e. cos ∠B = BC / AB
f. tan ∠B = AC / BC
11.
a. Schuine zijde
b. Overstaande rechthoekszijde van ∠D
c. Met de sinus kun je hoek D berekenen.
d. ∠D ≈ 62º
12.
a. Gebruik sin ∠L om de hoek te berekenen.
b. ∠L ≈ 55,4º
13.
Tip:
Onderzoek bij de volgende opgaven eerst of je de sin, cos of tan kunt gebruiken. Heb je 2 rechthoekszijden? Gebruik dan de tan.
∠D = 77ºOnderzoek bij de volgende opgaven eerst of je de sin, cos of tan kunt gebruiken. Heb je 2 rechthoekszijden? Gebruik dan de tan.
14.
∠T ≈ 49º
15.
Tip:
Om de hoeken in graden te berekenen gebruik we de sin-1, cos-1 en tan-1 op je rekenmachine.
∠A ≈ 23,58ºOm de hoeken in graden te berekenen gebruik we de sin-1, cos-1 en tan-1 op je rekenmachine.
∠B ≈ 56,98º
∠C ≈ 12,15º
16.
∠K ≈ 41º
∠L ≈ 28º
∠M ≈ 23º
17.
Tip:
Er zijn 2 rechthoekszijden gegeven dus we gebruiken dan de tan.
De zonnehoek is 54,7º.Er zijn 2 rechthoekszijden gegeven dus we gebruiken dan de tan.
18.
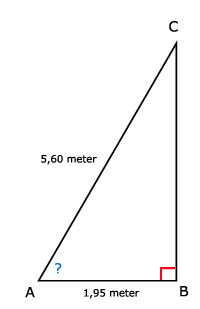
Tip:
De aanliggende rechthoekszijde en de schuine zijde horende bij hoek A zijn gegeven. Gebruik dan dus de cosinus.
a. Cos (∠A) = AB / AC = 1,95 / 5,6. De hellingshoek is dan 69,6º.De aanliggende rechthoekszijde en de schuine zijde horende bij hoek A zijn gegeven. Gebruik dan dus de cosinus.
b. Ja, de ladder staat prima.

19.
b. Hoek bij B is 70,53º
20.
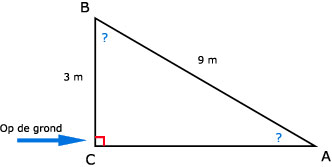
Tip:
Maak een schets en draai de driehoek zo dat de rechte hoek altijd "op de grond" ligt.
Bij a. De overstaande rechthoekszijde en de schuine zijde horende bij hoek A zijn gegeven. Gebruik dan dus de sinus.
Bij b. De aanliggende rechthoekszijde en de schuine zijde horende bij hoek B zijn gegeven. Gebruik dan dus de cosinus.
a. De dakhelling is 19,47ºMaak een schets en draai de driehoek zo dat de rechte hoek altijd "op de grond" ligt.
Bij a. De overstaande rechthoekszijde en de schuine zijde horende bij hoek A zijn gegeven. Gebruik dan dus de sinus.
Bij b. De aanliggende rechthoekszijde en de schuine zijde horende bij hoek B zijn gegeven. Gebruik dan dus de cosinus.
b. Hoek bij B is 70,53º

20.
Tip:
Reken eerst alles om naar cm.
Alleen helling C voldoet aan de eisen. Tan(∠C) ≈ 5,30º.Reken eerst alles om naar cm.
Andere paragrafen:
9.1. Berekeningen met de tangens (1 t/m 8)
9.2. Hoeken berekenen met sinus, cosinus en tangens (9 t/m 20)
9.3. Zijden berekenen met sinus, cosinus en tangens (21 t/m 32)
9.4. Zijden en hoeken berekenen (33 t/m 47)
9.5. Gemengde opgaven (48 t/m 64)
9.1. Berekeningen met de tangens (1 t/m 8)
9.2. Hoeken berekenen met sinus, cosinus en tangens (9 t/m 20)
9.3. Zijden berekenen met sinus, cosinus en tangens (21 t/m 32)
9.4. Zijden en hoeken berekenen (33 t/m 47)
9.5. Gemengde opgaven (48 t/m 64)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


