TIP: Wil je ook toegang tot meer dan 17.100 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 3.1 Lineaire formules HAVO/VWO 2
Boek: Getal & Ruimte - Lineaire formules en vergelijkingen HAVO/VWO 2 (deel 1) opgaven 1 t/m 12, 2013, 10e editie
1.
a. Invullen x = -2 levert: y = 1
b.
c. Je krijgt de punten op de grafiek: (-2,1), (-1;1,5), (0,2), (1;2,5), (2,3), (3;3,5), (4,4)
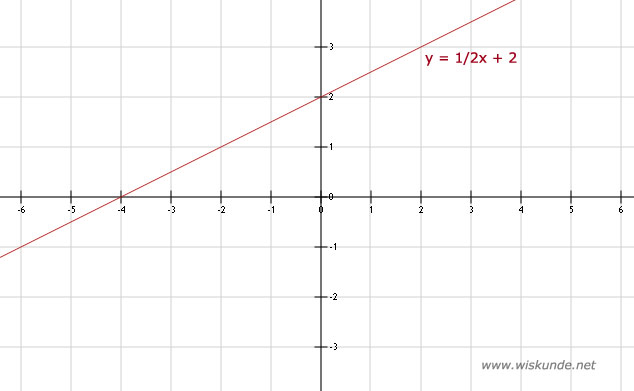
2.
b.
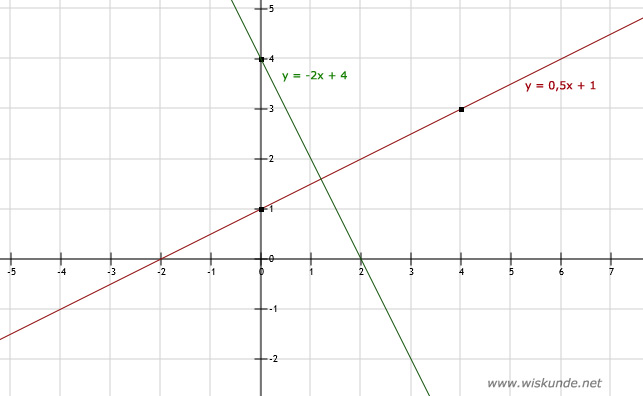
3.
Zie afbeelding
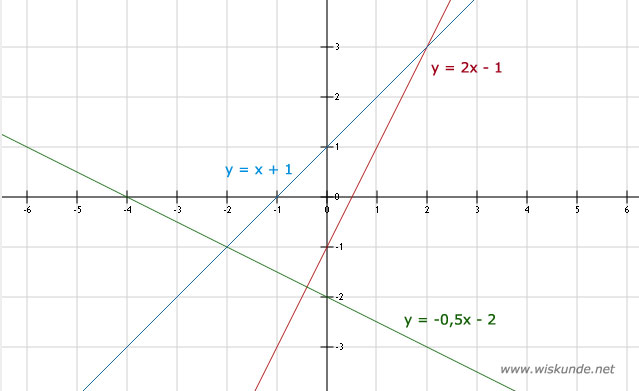
4.
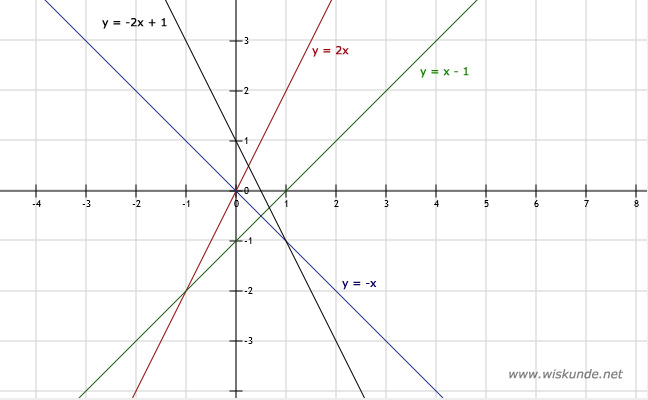
5.
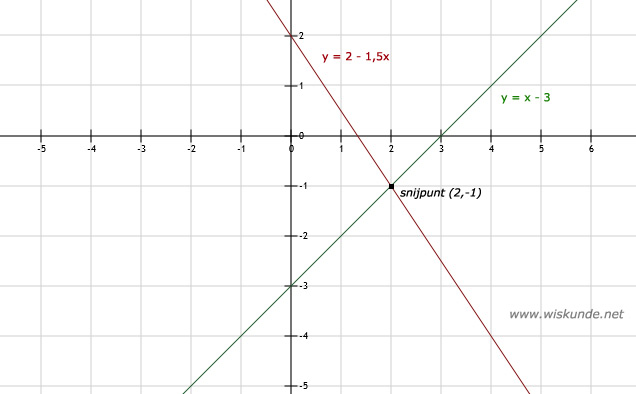
b. Het snijpunt van deze 2 lijnen is: (2,-1)
6.
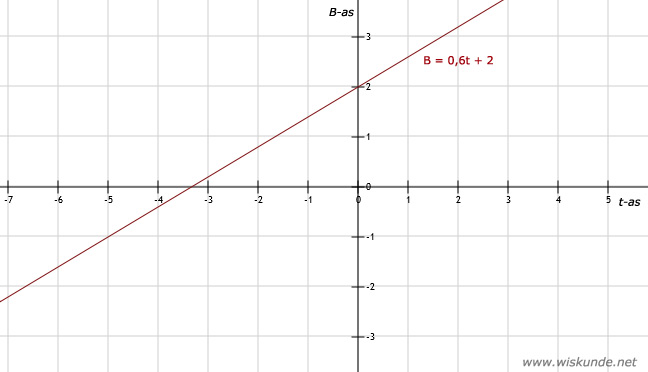
b. Bij t = 2 krijg je als B-waarde 3,2. Dat tekent lastig in een assenstelsel want het is geen exact roosterpunt.
Nog een goede waarde is bij t = 10 of t = -5.
c. Zie afbeelding
7.
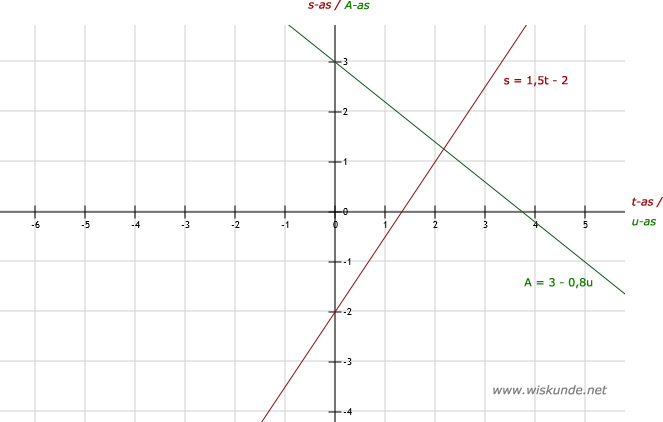
b. (groen)
8.
a. Er bestaan geen negatieve kwartieren.
b. Zie afbeelding
c. Zie afbeelding
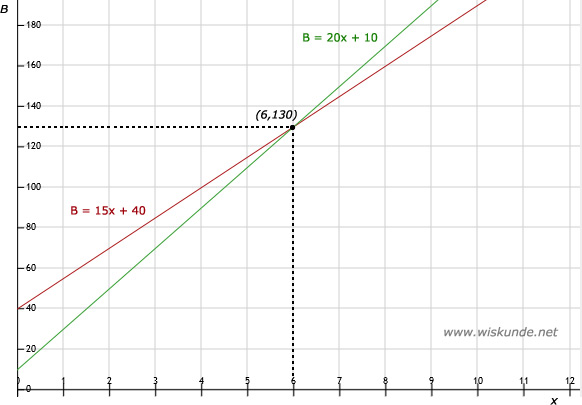
d. Snijpunt is (6,130)
De bedrijven zijn even duur bij 6 kwartier werken (90 minuten). Je betaalt dan bij beide 130,- euro.
9.
x = 5 invullen levert: y = 3⋅5 - 1 = 14
Je krijgt dan het punt op de grafiek: (5,14)
10.
A(5,14) invullen, levert: 14 = 3⋅5 - 1 => 14 = 14, ja dit punt ligt op de grafiek.
b.
B(9,26) invullen, levert: 26 = 3⋅9 - 1 => 26 = 26, ja dit punt ligt op de grafiek.
C(30,90) invullen, levert: 90 = 3⋅30 - 1 => 90 ≠ 89, nee dit punt ligt NIET op de grafiek.
D(-3,-10) invullen, levert: -10 = 3⋅-3 - 1 => -10 = -10, ja dit punt ligt op de grafiek.
c. y = -16
a. Invullen x = -2 levert: y = 1
b.
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 |

2.
Tip:
Kies in de tabel altijd x = 0. Dit rekent altijd makkelijk.
a. Kies in de tabel altijd x = 0. Dit rekent altijd makkelijk.
| x | 0 | 4 |
| y | 1 | 3 |
b.
| x | 0 | 4 |
| y | 4 | -4 |

3.
Zie afbeelding

4.
Tip:
Kies 2 punten per lijn en teken dan de lijn.
Zie afbeelding
Kies 2 punten per lijn en teken dan de lijn.

5.
Tip:
Bij x = 0 heb je het snijpunt met de y-as.
a. Zie afbeeldingBij x = 0 heb je het snijpunt met de y-as.
b. Het snijpunt van deze 2 lijnen is: (2,-1)

6.
Tip:
Het is handig om 2 punten te kiezen voor een lijn die beide wel roosterpunten zijn.
In deze opgave hebben we een t-as en een B-as i.p.v. een x-as en y-as. Maar het komt op hetzelfde neer.
a. Het is handig om 2 punten te kiezen voor een lijn die beide wel roosterpunten zijn.
In deze opgave hebben we een t-as en een B-as i.p.v. een x-as en y-as. Maar het komt op hetzelfde neer.
| t | 0 | 5 |
| B | 2 | 5 |
b. Bij t = 2 krijg je als B-waarde 3,2. Dat tekent lastig in een assenstelsel want het is geen exact roosterpunt.
Nog een goede waarde is bij t = 10 of t = -5.
c. Zie afbeelding

7.
Tip:
Ik heb ze nu even in 1 plaatje gedaan.
a. (rood)Ik heb ze nu even in 1 plaatje gedaan.
| t | 0 | 4 |
| s | -2 | 4 |
b. (groen)
| u | 0 | 5 |
| A | 3 | -1 |

8.
a. Er bestaan geen negatieve kwartieren.
b. Zie afbeelding
c. Zie afbeelding
d. Snijpunt is (6,130)
De bedrijven zijn even duur bij 6 kwartier werken (90 minuten). Je betaalt dan bij beide 130,- euro.

9.
x = 5 invullen levert: y = 3⋅5 - 1 = 14
Je krijgt dan het punt op de grafiek: (5,14)
10.
Tip:
Vul de punten in de formule in en kijk of het klopt.
a.Vul de punten in de formule in en kijk of het klopt.
A(5,14) invullen, levert: 14 = 3⋅5 - 1 => 14 = 14, ja dit punt ligt op de grafiek.
b.
B(9,26) invullen, levert: 26 = 3⋅9 - 1 => 26 = 26, ja dit punt ligt op de grafiek.
C(30,90) invullen, levert: 90 = 3⋅30 - 1 => 90 ≠ 89, nee dit punt ligt NIET op de grafiek.
D(-3,-10) invullen, levert: -10 = 3⋅-3 - 1 => -10 = -10, ja dit punt ligt op de grafiek.
c. y = -16
11.
P(4,-2) invullen, levert: -2 = -¾⋅4 + 1 =>
-2 = -3 + 1 =>
-2 = -2, ja dit punt ligt op de grafiek.
Q(20,16) invullen, levert: 16 = -¾⋅20 + 1 =>
16 = -15 + 1 =>
16 ≠ -14, nee dit punt ligt NIET op de grafiek.
R(-100,76) invullen, levert: 76 = -¾⋅-100 + 1 =>
76 = 75 + 1 =>
76 = 76, ja dit punt ligt op de grafiek.
b. S(-8,y) invullen, levert: y = -¾⋅-8 + 1 =>
y = 6 + 1 = 7
12.
A(-4,p) invullen, levert: p = 1/4⋅-4 - 1 =>
p = -1 - 1 =>
p = -2
b.
B(5,q) invullen, levert: q = -3⋅5 + 8 =>
q = -15 + 8 =>
q = -7
c.
C(2,8) invullen, levert: 8 = a⋅2 =>
2a = 8 =>
a = 4
d.
D(-4,18) invullen, levert: 18 = -2⋅-4 + b =>
18 = 8 + b =>
b = 10
Tip:
Het punt R(-100,76) is onmogelijk te tekenen in een assenstelsel. Vandaar dat je het moet berekenen.
a.Het punt R(-100,76) is onmogelijk te tekenen in een assenstelsel. Vandaar dat je het moet berekenen.
P(4,-2) invullen, levert: -2 = -¾⋅4 + 1 =>
-2 = -3 + 1 =>
-2 = -2, ja dit punt ligt op de grafiek.
Q(20,16) invullen, levert: 16 = -¾⋅20 + 1 =>
16 = -15 + 1 =>
16 ≠ -14, nee dit punt ligt NIET op de grafiek.
R(-100,76) invullen, levert: 76 = -¾⋅-100 + 1 =>
76 = 75 + 1 =>
76 = 76, ja dit punt ligt op de grafiek.
b. S(-8,y) invullen, levert: y = -¾⋅-8 + 1 =>
y = 6 + 1 = 7
12.
Tip:
Vul nu voor de y-waarde in: p, q of a. Zoals je gewend bent.
a.Vul nu voor de y-waarde in: p, q of a. Zoals je gewend bent.
A(-4,p) invullen, levert: p = 1/4⋅-4 - 1 =>
p = -1 - 1 =>
p = -2
b.
B(5,q) invullen, levert: q = -3⋅5 + 8 =>
q = -15 + 8 =>
q = -7
c.
C(2,8) invullen, levert: 8 = a⋅2 =>
2a = 8 =>
a = 4
d.
D(-4,18) invullen, levert: 18 = -2⋅-4 + b =>
18 = 8 + b =>
b = 10
Andere paragrafen:
3.1. Lineaire formules (1 t/m 12)
3.2. Lineaire formule opstellen (13 t/m 31)
3.3. Som- en verschilgrafieken (32 t/m 42)
3.4. De balansmethode (43 t/m 59)
3.5. Vergelijkingen oplossen (60 t/m 79)
3.1. Lineaire formules (1 t/m 12)
3.2. Lineaire formule opstellen (13 t/m 31)
3.3. Som- en verschilgrafieken (32 t/m 42)
3.4. De balansmethode (43 t/m 59)
3.5. Vergelijkingen oplossen (60 t/m 79)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


