TIP: Wil je ook toegang tot meer dan 17.100 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 3.2 Lineaire formule opstellen HAVO/VWO 2
Boek: Getal & Ruimte - Lineaire formules en vergelijkingen HAVO/VWO 2 (deel 1) opgaven 13 t/m 31, 2013, 10e editie
13.
b. y = -2x + 7
14.
a. a = -0,3 b = 2,6
b. a = 5 b = -1,4
c. a = 1 b = 8
d. a = -1 b = 1
e. a = 1 b = 0
f. a = -4 b = 0
g. a = 0 b = 2
h. a = 2 b = 3
i. a = -1 b = -9
15.
b. rc = 3
c. Ga je 1 naar rechts, dan ga je 3 omhoog.
16.
a. Rc = -1/2 en snijpunt met de y-as: (0,-4)
b. Ga je 1 naar rechts, dan ga je -1/2 omhoog, ofwel 1/2 omlaag.
17.
Snijden in de y-as: y = 2x + 2 en y = 0,5x + 2.
Dat zie je omdat ze gelijke b-waarde hebben (y = ax + b). De waarde van b is dus 2.
b.
Evenwijdig zijn: y = 0,5x - 3 en y = 0,5x + 2.
Dat zie je omdat ze gelijke a-waarde hebben (y = ax + b). De waarde van a is dus 0,5.
18.
y = 5x + 7 en y = 5x + 3 (i.v.m. 5)
y = -0,2x + 1 en y = -0,2x + 3 (i.v.m. -0,2)
b. Hetzelfde snijpunt met de y-as:
y = 5x + 7 en y = -4x + 7 (i.v.m. 7)
y = 4x + 3 en y = 5x + 3 en y = -0,2x + 3 (i.v.m. 3)
19.
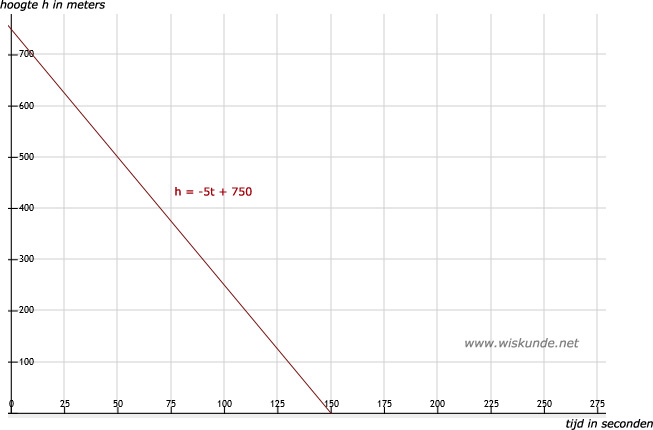
b. t = 50 invullen levert: h = -5 ⋅ 50 + 750 = 500 (meter)
t = 60 invullen levert: h = -5 ⋅ 60 + 750 = 450 (meter)
c. Zie afbeelding
d. Bij t = 150 geldt: h = -5 ⋅ 150 + 750 = -750 + 750 = 0 (meter)
Dus bij t = 150 (seconden) is de hoogte gelijk aan 0 (meter). Je krijgt dan het punt (150,0). Dit is het snijpunt met de x-as.
e. Per seconde daalt de parachute 5 meter.
20.
b. 2 omhoog, dus a = 2
c. y = 2x - 1
d. (0,3), dus b = 3
e. 1 omlaag, dus a = -1
f. y = -x + 3
21.
a. (0,1), dus b = 1
b. 3/5 omhoog, dus a = 3/5
c. y = 3/5x + 1
22.
Formule lijn m: y = 2/5x + 1
Formule lijn n: y = -2x + 4
Tip:
De basisvorm van een formule is: y = ax + b.
a. y = 15x + 20De basisvorm van een formule is: y = ax + b.
b. y = -2x + 7
14.
a. a = -0,3 b = 2,6
b. a = 5 b = -1,4
c. a = 1 b = 8
d. a = -1 b = 1
e. a = 1 b = 0
f. a = -4 b = 0
g. a = 0 b = 2
h. a = 2 b = 3
i. a = -1 b = -9
15.
Tip:
Bij y = ax + b, snijpunt met de y-as is (0,b)
a is de richtingscoefficient ofwel de helling van de lijn
a. Snijpunt met de y-as: (0,2)Bij y = ax + b, snijpunt met de y-as is (0,b)
a is de richtingscoefficient ofwel de helling van de lijn
b. rc = 3
c. Ga je 1 naar rechts, dan ga je 3 omhoog.
16.
a. Rc = -1/2 en snijpunt met de y-as: (0,-4)
b. Ga je 1 naar rechts, dan ga je -1/2 omhoog, ofwel 1/2 omlaag.
17.
Tip:
Grafieken die dezelfde a-waarde hebben (y = ax + b) zijn evenwijdig. Ze hebben dan gelijke richtingscoefficiënt.
Grafieken die dezelfde b-waarde hebben (y = ax + b) snijden elkaar in de y-as in punt (0,b).
a.Grafieken die dezelfde a-waarde hebben (y = ax + b) zijn evenwijdig. Ze hebben dan gelijke richtingscoefficiënt.
Grafieken die dezelfde b-waarde hebben (y = ax + b) snijden elkaar in de y-as in punt (0,b).
Snijden in de y-as: y = 2x + 2 en y = 0,5x + 2.
Dat zie je omdat ze gelijke b-waarde hebben (y = ax + b). De waarde van b is dus 2.
b.
Evenwijdig zijn: y = 0,5x - 3 en y = 0,5x + 2.
Dat zie je omdat ze gelijke a-waarde hebben (y = ax + b). De waarde van a is dus 0,5.
18.
Tip:
Het getal voor de x noemen we ook wel de richtingscoefficiënt.
a. Evenwijdig zijn:Het getal voor de x noemen we ook wel de richtingscoefficiënt.
y = 5x + 7 en y = 5x + 3 (i.v.m. 5)
y = -0,2x + 1 en y = -0,2x + 3 (i.v.m. -0,2)
b. Hetzelfde snijpunt met de y-as:
y = 5x + 7 en y = -4x + 7 (i.v.m. 7)
y = 4x + 3 en y = 5x + 3 en y = -0,2x + 3 (i.v.m. 3)
19.
Tip:
De grafiek heeft geen negatieve assen. Want negatieve seconden en negatieve hoogte bestaan niet.
a. t = 0 invullen levert: h = -5 ⋅ 0 + 750 = 750 (meter)De grafiek heeft geen negatieve assen. Want negatieve seconden en negatieve hoogte bestaan niet.
b. t = 50 invullen levert: h = -5 ⋅ 50 + 750 = 500 (meter)
t = 60 invullen levert: h = -5 ⋅ 60 + 750 = 450 (meter)
c. Zie afbeelding
d. Bij t = 150 geldt: h = -5 ⋅ 150 + 750 = -750 + 750 = 0 (meter)
Dus bij t = 150 (seconden) is de hoogte gelijk aan 0 (meter). Je krijgt dan het punt (150,0). Dit is het snijpunt met de x-as.
e. Per seconde daalt de parachute 5 meter.

20.
Tip:
Bij y = ax + b, snijpunt met de y-as is (0,b).
a is de richtingscoefficient ofwel de helling van de lijn.
Ga je 1 naar rechts, dan ga je a omhoog.
Is a negatief? Dan ga je omlaag.
a. (0,-1), dus b = -1Bij y = ax + b, snijpunt met de y-as is (0,b).
a is de richtingscoefficient ofwel de helling van de lijn.
Ga je 1 naar rechts, dan ga je a omhoog.
Is a negatief? Dan ga je omlaag.
b. 2 omhoog, dus a = 2
c. y = 2x - 1
d. (0,3), dus b = 3
e. 1 omlaag, dus a = -1
f. y = -x + 3
21.
a. (0,1), dus b = 1
b. 3/5 omhoog, dus a = 3/5
c. y = 3/5x + 1
22.
Tip:
Basisformule: y = ax + b
Stel a = verticaal / horizontaal
Zoek b: snijpunt met de y-as
Formule lijn l: y = 1/2x - 2Basisformule: y = ax + b
Stel a = verticaal / horizontaal
Zoek b: snijpunt met de y-as
Formule lijn m: y = 2/5x + 1
Formule lijn n: y = -2x + 4
23.
1) Stel y = ax + b
2) Door (0,1) dus b = 1
3) a = rc = verticaal / horizontaal = 1/3
4) Dus y = 1/3x + 1
Formule lijn l: opstellen:
1) Stel y = ax + b
2) Door (0,-3) dus b = -3
3) a = rc = verticaal / horizontaal = 2/3
4) Dus y = 2/3x - 3
Formule lijn m: opstellen:
1) Stel y = ax + b
2) Door (0,2) dus b = 2
3) a = rc = verticaal / horizontaal = -1/1 = -1
4) Dus y = -x + 2
24.
Formule lijn l: y = 3/5x + 3
Formule lijn m: y = -2/3x + 5
Formule lijn n: y = -x + 3
25.
b. s = -1½t + 4, alle andere lijnen gaan door (0,-4) of (0,-1½) dus de rc hoef je hier niet eens uit te rekenen.
26.
1) Stel A = ap + b
2) Door (0,30) dus b = 30
3) a = rc = verticaal / horizontaal = -5/1 = -5
4) Dus A = -5p + 30
Formule lijn k: opstellen:
1) Stel R = aq + b
2) Door (0,0) dus b = 0
3) a = rc = verticaal / horizontaal = 150/5 = 30
4) Dus R = 30q
Formule lijn p: opstellen:
1) Stel N = ax + b
2) Door (0,950) dus b = 950
3) a = rc = verticaal / horizontaal = 50/2 = 25
4) Dus N = 25x + 950
27.
Formule lijn m: S = -7,5t + 200
28.
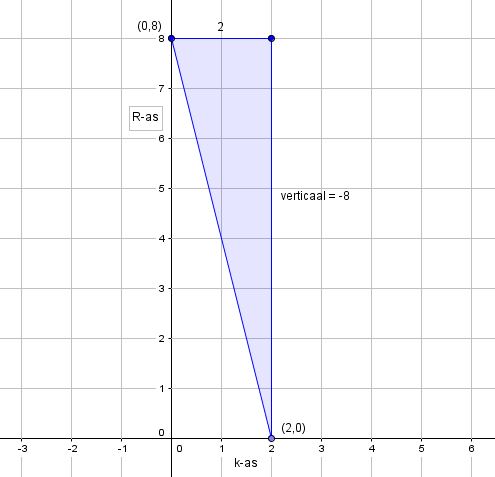
Formule van lijn m: R = -4k + 8
29.
1) Stel B = ak + b
2) Door (0,15) dus b = 15
3) a = rc = verticaal / horizontaal = 30/50 = 3/5 = 0,6
4) Dus B = 3/5k + 15
b = starttarief = 15
k = prijs per kilometer = 0,60
b.
B = 3/5k + 25
c.
B = (0,6 + 0,1)k + 25
B = 0,7k + 25
30.
b. D = -12t + 323
c. Bij het jaar 2016 hoort t = 9: D = -12*9 + 323 = 215
d. 21
31.
b. A = 1500t + 39.000
c. 2016 dan t = 16. Dus: A = 1500*16 + 39000 = 63.000
d. 9.900
Tip:
Bij y = ax + b:
a is de richtingscoëfficient van de lijn. Dus rcl = verticaal / horizontaal
b is het snijpunt met de y-as. Hierbij is de x gelijk aan 0. Dus snijpunt (0,b).
Formule lijn k: opstellen:Bij y = ax + b:
a is de richtingscoëfficient van de lijn. Dus rcl = verticaal / horizontaal
b is het snijpunt met de y-as. Hierbij is de x gelijk aan 0. Dus snijpunt (0,b).
1) Stel y = ax + b
2) Door (0,1) dus b = 1
3) a = rc = verticaal / horizontaal = 1/3
4) Dus y = 1/3x + 1
Formule lijn l: opstellen:
1) Stel y = ax + b
2) Door (0,-3) dus b = -3
3) a = rc = verticaal / horizontaal = 2/3
4) Dus y = 2/3x - 3
Formule lijn m: opstellen:
1) Stel y = ax + b
2) Door (0,2) dus b = 2
3) a = rc = verticaal / horizontaal = -1/1 = -1
4) Dus y = -x + 2
24.
Tip:
Bepaal a: zoek 2 roosterpunten en dan: a = verticaal / horizontaal
Bepaal b: snijpunt met de y-as.
Formule lijn k: y = 3/4x (de +0 schrijven we niet op)Bepaal a: zoek 2 roosterpunten en dan: a = verticaal / horizontaal
Bepaal b: snijpunt met de y-as.
Formule lijn l: y = 3/5x + 3
Formule lijn m: y = -2/3x + 5
Formule lijn n: y = -x + 3
25.
Tip:
Snijpunt met de y-as is (0,4). Dus je weet meteen b.
a. rcn = verticaal / horizontaal = -3/2 = -1,5Snijpunt met de y-as is (0,4). Dus je weet meteen b.
b. s = -1½t + 4, alle andere lijnen gaan door (0,-4) of (0,-1½) dus de rc hoef je hier niet eens uit te rekenen.
26.
Tip:
Let op, we hebben nu andere assen. De y-as correspondeert nu met de A-as, R-as en N-as.
Formule lijn m: opstellen:Let op, we hebben nu andere assen. De y-as correspondeert nu met de A-as, R-as en N-as.
1) Stel A = ap + b
2) Door (0,30) dus b = 30
3) a = rc = verticaal / horizontaal = -5/1 = -5
4) Dus A = -5p + 30
Formule lijn k: opstellen:
1) Stel R = aq + b
2) Door (0,0) dus b = 0
3) a = rc = verticaal / horizontaal = 150/5 = 30
4) Dus R = 30q
Formule lijn p: opstellen:
1) Stel N = ax + b
2) Door (0,950) dus b = 950
3) a = rc = verticaal / horizontaal = 50/2 = 25
4) Dus N = 25x + 950
27.
Tip:
De waarden voor 'b' van de basisvorm y = ax + b (ofwel S = at + b) lees je makkelijk af van de y-as.
Formule lijn l: S = 6t + 100De waarden voor 'b' van de basisvorm y = ax + b (ofwel S = at + b) lees je makkelijk af van de y-as.
Formule lijn m: S = -7,5t + 200
28.
Tip:
Maak een schets. Dan a = verticaal / horizontaal = -8 / 2 = -4
De verticale as is nu niet de y-as maar de R-as.
De horizontale as is nu niet de x-as maar de k-as.
Vandaar dus de basisformule: R = ak + b.
b = 8, want snijpunt met de verticale as is (0,8).Maak een schets. Dan a = verticaal / horizontaal = -8 / 2 = -4
De verticale as is nu niet de y-as maar de R-as.
De horizontale as is nu niet de x-as maar de k-as.
Vandaar dus de basisformule: R = ak + b.
Formule van lijn m: R = -4k + 8

29.
Tip:
Je kunt ook controleren of je formule goed is. Pak een punt dat op de lijn ligt (bijv. (50,45)) en vul deze in in de formule. En kijk of er links en rechts van het =-teken hetzelfde staat.
aJe kunt ook controleren of je formule goed is. Pak een punt dat op de lijn ligt (bijv. (50,45)) en vul deze in in de formule. En kijk of er links en rechts van het =-teken hetzelfde staat.
1) Stel B = ak + b
2) Door (0,15) dus b = 15
3) a = rc = verticaal / horizontaal = 30/50 = 3/5 = 0,6
4) Dus B = 3/5k + 15
b = starttarief = 15
k = prijs per kilometer = 0,60
b.
B = 3/5k + 25
c.
B = (0,6 + 0,1)k + 25
B = 0,7k + 25
30.
Tip:
Zie tabel: in de bovenste rij steeds +1 en in de onderste rij steeds -12. Dus de helling is -12.
a. 323 - 311 = 12 en ook 311 - 299 = 12 enz. Dus jaarlijks daalt de hoeveelheid met 12 discotheken.Zie tabel: in de bovenste rij steeds +1 en in de onderste rij steeds -12. Dus de helling is -12.
b. D = -12t + 323
c. Bij het jaar 2016 hoort t = 9: D = -12*9 + 323 = 215
d. 21
31.
Tip:
Boven is steeds +3 en onder steeds +4500.
Dat is hetzelfde als boven steeds +1 en onder steeds +1500. Dus a = 1500.
De 'b' volgt uit de waarde bij t = 0.
a. Toename artsen per jaar: 1500Boven is steeds +3 en onder steeds +4500.
Dat is hetzelfde als boven steeds +1 en onder steeds +1500. Dus a = 1500.
De 'b' volgt uit de waarde bij t = 0.
b. A = 1500t + 39.000
c. 2016 dan t = 16. Dus: A = 1500*16 + 39000 = 63.000
d. 9.900
Andere paragrafen:
3.1. Lineaire formules (1 t/m 12)
3.2. Lineaire formule opstellen (13 t/m 31)
3.3. Som- en verschilgrafieken (32 t/m 42)
3.4. De balansmethode (43 t/m 59)
3.5. Vergelijkingen oplossen (60 t/m 79)
3.1. Lineaire formules (1 t/m 12)
3.2. Lineaire formule opstellen (13 t/m 31)
3.3. Som- en verschilgrafieken (32 t/m 42)
3.4. De balansmethode (43 t/m 59)
3.5. Vergelijkingen oplossen (60 t/m 79)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


