TIP: Wil je ook toegang tot meer dan 17.100 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 3.5 Vergelijkingen oplossen HAVO/VWO 2
Boek: Getal & Ruimte - Lineaire formules en vergelijkingen HAVO/VWO 2 (deel 1) opgaven 60 t/m 79, 2013, 10e editie
60.
Nu links en rechts -3x
2x + 2 = 6
Nu links en rechts -2
2x = 4
Nu links en rechts :2
x = 4/2 = 2
61.
62.
63.
64.
Vat A => 15 + 0,5x (rechterlid)
Vat B => 10 + 1,5x (linkerlid)
b.
10 + 1,5x = 15 + 0,5x
Nu links en rechts -0,5x
10 + x = 15
Nu links en rechts -10
x = 5
c.
Na 5 minuten staat het water in beide vaten even hoog.
Hoogte van het water is dan: 15 + 0,5⋅5 = 15 + 2,5 = 17,5 cm
65.
a.
Kosten = 2,50 + 0,05 * 400 = 22,50 euro
b.
4,75 + 0,02a = 14,75
0,02a = 10
a = 500 (MB)
c.
Los op:
2,50 + 0,05a = 4,75 + 0,02a
Nu links en rechts -0,02a
0,03a + 2,50 = 4,75
Nu links en rechts -2,50
0,03a = 2,25
Nu links en rechts :0,03
a = 75
Bij een gebruik van 75MB zijn beide bedrijven even duur.
66.
b. Even duur is bij het snijpunt. Dat is bij d = 10. En een prijs van 300,=. Dus bij het punt (10,300).
c.
30d = 25d + 50
Nu links en rechts -25d
5d = 50
Nu links en rechts :5
d = 10
Je ziet dat het dus klopt! Bij d = 10 (dagen) zijn beide bedrijven even duur. De prijs is dan 300,=.
67.
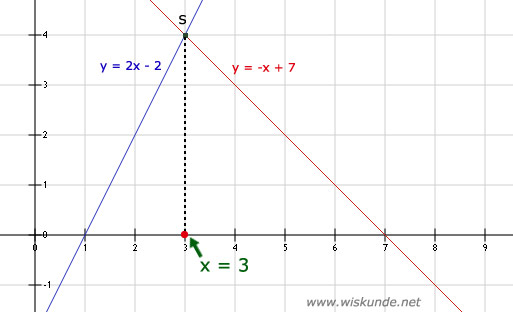
Snijpunt: S(3,4)
b.
2x - 2 = -x + 7
3x = 9
x = 3 (zie rode stip in afbeelding)
c.
De oplossing x = 3 is de x-coördinaat van het snijpunt S.
68.
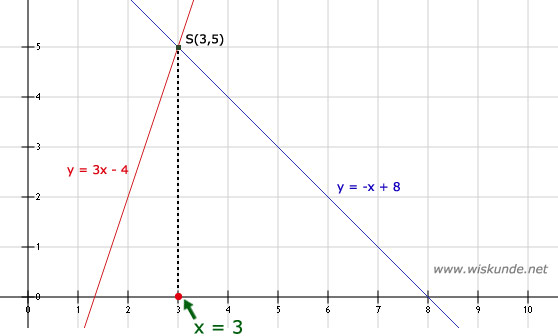
3x - 4 = -x + 8
4x = 12
x = 3
b.
Voor de y-coördinaat van S: x = 3 invullen in y = -x + 8 levert:
y = -3 + 8 = 5
Dus het snijpunt van de 2 grafieken: S(3,5)
69.
b. -10x + 5
c. 6x - 27
d. -27x + 6
e. -6x + 2
f. -4 + 5x
Tip:
Controleer de gevonden oplossing van x:
5⋅2 + 2 = 3⋅2 + 6
10 + 2 = 6 + 6
12 = 12
Ja, het klopt!
5x + 2 = 3x + 6Controleer de gevonden oplossing van x:
5⋅2 + 2 = 3⋅2 + 6
10 + 2 = 6 + 6
12 = 12
Ja, het klopt!
Nu links en rechts -3x
2x + 2 = 6
Nu links en rechts -2
2x = 4
Nu links en rechts :2
x = 4/2 = 2
61.
Tip:
Zorg ervoor dat de variabele x in het rechterlid verdwijnt en dat de gewone getallen in het linkerlid verdwijnen.
Deel als laatste stap links en rechts door het getal voor de x.
Zorg ervoor dat de variabele x in het rechterlid verdwijnt en dat de gewone getallen in het linkerlid verdwijnen.
Deel als laatste stap links en rechts door het getal voor de x.
|
a. 7x - 15 = 5x + 5 Nu links en rechts -5x 2x - 15 = 5 Nu links en rechts +15 2x = 20 Nu links en rechts :2 x = 20/2 = 10 b. -3x + 18 = x + 26 Nu links en rechts -x -4x + 18 = 26 Nu links en rechts -18 -4x = 8 Nu links en rechts :-4 x = 8/-4 = -2 c. 8a - 15 = 3a Nu links en rechts -3a 5a - 15 = 0 Nu links en rechts +15 5a = 15 Nu links en rechts :5 a = 15/5 = 3 |
d. 1,1x + 2,7 = 2,1x + 3,7 Nu links en rechts -2,1x -x + 2,7 = 3,7 Nu links en rechts -2,7 -x = 1 Nu links en rechts :-1 x = 1/-1 = -1 e. 7p + 5 = -3p - 15 Nu links en rechts +3p 10p + 5 = -15 Nu links en rechts -5 10p = -20 Nu links en rechts :10 p = -20/10 = -2 f. 5x - 4 = -x - 4 Nu links en rechts +x 6x - 4 = -4 Nu links en rechts +4 6x = 0 Nu links en rechts :6 x = 0/6 = 0 |
62.
Tip:
Zorg ervoor dat alleen in het linkerlid de variabele overblijft.
De variabele is vaak een x, maar kan bijvoorbeeld ook aan a, b of y zijn.
Zorg ervoor dat alleen in het linkerlid de variabele overblijft.
De variabele is vaak een x, maar kan bijvoorbeeld ook aan a, b of y zijn.
|
a. 3x + 7 = 2x - 6 Nu links en rechts -2x x + 7 = -6 Nu links en rechts -7 x = -13 b. -5y - 3 = 2y - 3 Nu links en rechts -2y -7y - 3 = -3 Nu links en rechts +3 -7y = 0 Nu links en rechts :-7 y = 0/-7 = 0 c. 8 - 3x = 15 - x Nu links en rechts +x 8 - 2x = 15 Nu links en rechts -8 -2x = 7 Nu links en rechts :-2 x = 7/-2 = -3½ |
d. 17 + 5x = 2x + 5 Nu links en rechts -2x 17 + 3x = 5 Nu links en rechts -17 3x = -12 Nu links en rechts :3 x = -12/3 = -4 e. 7x = 8 - x Nu links en rechts +x 8x = 8 Nu links en rechts :8 x = 8/8 = 1 f. 7 + 2t = 9 - 2t Nu links en rechts +2t 7 + 4t = 9 Nu links en rechts -7 4t = 2 Nu links en rechts :4 t = 2/4 = 1/2 |
63.
Tip:
Je weet: 2 + 3 = 4 + 1, dus ook geldt dan: 4 + 1 = 2 + 3. Je mag het dus omdraaien. Gebruik dit bij opgave c:.
Je weet: 2 + 3 = 4 + 1, dus ook geldt dan: 4 + 1 = 2 + 3. Je mag het dus omdraaien. Gebruik dit bij opgave c:.
|
a. 4 + 2x = x + 3 Nu links en rechts -x 4 + x = 3 Nu links en rechts -4 x = -1 b. -5x + 17 = -4 - 2x Nu links en rechts +2x -3x + 17 = -4 Nu links en rechts -17 -3x = -21 Nu links en rechts :-3 x = -21/-3 = 7 c. 21 = 7q - 35 (omdraaien) 7q - 35 = 21 Nu links en rechts +35 7q = 56 Nu links en rechts :7 q = 56/7 = 8 |
d. 21d + 4 = 19d - 34 Nu links en rechts -19d 2d + 4 = -34 Nu links en rechts -4 2d = -38 Nu links en rechts :2 d = -38/2 = -19 e. 14x - 11 = 11x + 14 Nu links en rechts -11x 3x - 11 = 14 Nu links en rechts +11 3x = 25 Nu links en rechts :3 x = 25/3 = 8 1/3 f. 17 - x = -9 + x Nu links en rechts -x 17 - 2x = -9 Nu links en rechts -17 -2x = -26 Nu links en rechts :-2 x = -26/-2 = 13 |
64.
Tip:
Bij dit soort vergelijkingen zoek je naar de oplossing (x-waarde) waarbij er sprake is van een evenwicht.
a. Bij dit soort vergelijkingen zoek je naar de oplossing (x-waarde) waarbij er sprake is van een evenwicht.
Vat A => 15 + 0,5x (rechterlid)
Vat B => 10 + 1,5x (linkerlid)
b.
10 + 1,5x = 15 + 0,5x
Nu links en rechts -0,5x
10 + x = 15
Nu links en rechts -10
x = 5
c.
Na 5 minuten staat het water in beide vaten even hoog.
Hoogte van het water is dan: 15 + 0,5⋅5 = 15 + 2,5 = 17,5 cm
65.
a.
Kosten = 2,50 + 0,05 * 400 = 22,50 euro
b.
4,75 + 0,02a = 14,75
0,02a = 10
a = 500 (MB)
c.
Los op:
2,50 + 0,05a = 4,75 + 0,02a
Nu links en rechts -0,02a
0,03a + 2,50 = 4,75
Nu links en rechts -2,50
0,03a = 2,25
Nu links en rechts :0,03
a = 75
Bij een gebruik van 75MB zijn beide bedrijven even duur.
66.
Tip:
Bij a: Trek een verticale lijn bij d = 6.
Even duur is bij het snijpunt.
a. De Hondt is goedkoper. Bij d = 6 ligt De Hondt onder Van Leeuwen. Kort: groen ligt onder rood.Bij a: Trek een verticale lijn bij d = 6.
Even duur is bij het snijpunt.
b. Even duur is bij het snijpunt. Dat is bij d = 10. En een prijs van 300,=. Dus bij het punt (10,300).
c.
30d = 25d + 50
Nu links en rechts -25d
5d = 50
Nu links en rechts :5
d = 10
Je ziet dat het dus klopt! Bij d = 10 (dagen) zijn beide bedrijven even duur. De prijs is dan 300,=.
67.
Tip:
Voor de x-coördinaat van het snijpunt S:
Los op: 2x - 2 = -x + 7
a.Voor de x-coördinaat van het snijpunt S:
Los op: 2x - 2 = -x + 7
Snijpunt: S(3,4)
b.
2x - 2 = -x + 7
3x = 9
x = 3 (zie rode stip in afbeelding)
c.
De oplossing x = 3 is de x-coördinaat van het snijpunt S.

68.
Tip:
- Voor de x-coördinaat van het snijpunt S:
Los op: 3x - 4 = -x + 8
- Voor de y-coördinaat van het snijpunt S:
Vul de gevonden x in 1 van de 2 formules. Kies de makkelijkste.
a.- Voor de x-coördinaat van het snijpunt S:
Los op: 3x - 4 = -x + 8
- Voor de y-coördinaat van het snijpunt S:
Vul de gevonden x in 1 van de 2 formules. Kies de makkelijkste.
3x - 4 = -x + 8
4x = 12
x = 3
b.
Voor de y-coördinaat van S: x = 3 invullen in y = -x + 8 levert:
y = -3 + 8 = 5
Dus het snijpunt van de 2 grafieken: S(3,5)

69.
Tip:
Haakjes wegwerken: a(b + c) = ab + ac
a. 5x + 40Haakjes wegwerken: a(b + c) = ab + ac
b. -10x + 5
c. 6x - 27
d. -27x + 6
e. -6x + 2
f. -4 + 5x
70.
71.
72.
73.
*
74.
2/5 x = 6
Nu links en rechts :2/5
x = 6 / (2/5)
x = 6 * (5/2)
x = 30/2
x = 15
b.
2/5 x = 6
Nu links en rechts *5 (keer 5)
5 ⋅ 2/5 x = 5 ⋅ 6
10/5 x = 30
2x = 30
Nu links en rechts :2
x = 30/2 = 15
75.
76.
77.
Zie afbeelding

78.
79.
Tip:
Volg het werkschema:
- werk eerst de haakjes weg
- neem eventueel gelijksoortige termen samen
- breng de x naar links
- breng de getallen naar rechts
- deel als laatste stap door het getal voor de x
Volg het werkschema:
- werk eerst de haakjes weg
- neem eventueel gelijksoortige termen samen
- breng de x naar links
- breng de getallen naar rechts
- deel als laatste stap door het getal voor de x
|
a. 5(x - 1) = 2x + 4 Nu haakjes wegwerken: 5x - 5 = 2x + 4 Nu links en rechts -2x 3x - 5 = 4 Nu links en rechts +5 3x = 9 Nu links en rechts :3 x = 9/3 = 3 b. -2(x - 2) = 8 - 3x Nu haakjes wegwerken: -2x + 4 = 8 - 3x Nu links en rechts +3x x + 4 = 8 Nu links en rechts -4 x = 4 c. 3(x - 4) + 2 = 5x + 1 Nu haakjes wegwerken: 3x - 12 + 2 = 5x + 1 Nu gelijksoortige termen samen nemen: 3x - 10 = 5x + 1 Nu links en rechts -5x -2x - 10 = 1 Nu links en rechts +10 -2x = 11 Nu links en rechts :-2 x = 11/-2 = -5 1/2 d. -3(x + 1) - 7 = 2x Nu haakjes wegwerken: -3x - 3 - 7 = 2x -3x - 10 = 2x Nu links en rechts -2x -5x - 10 = 0 Nu links en rechts +10 -5x = 10 Nu links en rechts :-5 x = 10/-5 = -2 |
e. 4x + 2x = x + 7 6x = x + 7 Nu links en rechts -x 5x = 7 Nu links en rechts :5 x = 7/5 = 1 2/5 f. 4(2x + 1) = 5x + 7 Nu haakjes wegwerken: 8x + 4 = 5x + 7 Nu links en rechts -5x 3x + 4 = 7 Nu links en rechts -4 3x = 3 Nu links en rechts :3 x = 3/3 = 1 g. 5(x - 2) = 3(2x + 2) + 2 Nu haakjes wegwerken: 5x - 10 = 6x + 6 + 2 5x - 10 = 6x + 8 Nu links en rechts -6x -x - 10 = 8 Nu links en rechts +10 -x = 18 Nu links en rechts :-1 x = -18 h. 4 - 3x = 5 - (x - 2) (Let op: Er staat een verborgen -1 voor de haakjes!) Nu haakjes wegwerken: 4 - 3x = 5 - x + 2 4 - 3x = 7 - x Nu links en rechts +x 4 - 2x = 7 Nu links en rechts -4 -2x = 3 Nu links en rechts :-2 x = 3/-2 = -1 1/2 |
71.
Tip:
Gebruik het werkschema uit je boek.
Gebruik het werkschema uit je boek.
|
a. 2(x - 3) = 3(2x + 10) Nu haakjes wegwerken: 2x - 6 = 6x + 30 Nu links en rechts -6x -4x - 6 = 30 Nu links en rechts +6 -4x = 36 Nu links en rechts :-4 x = 36/-4 = -9 b. 6(p + 1) = 5(p - 1,2) Nu haakjes wegwerken: 6p + 6 = 5p - 6 Nu links en rechts -5p p + 6 = -6 Nu links en rechts -6 p = -12 c. 3(x + 6) = 6(x - 3) + x Nu haakjes wegwerken: 3x + 18 = 6x - 18 + x Nu gelijksoortige termen samen nemen: 3x + 18 = 7x - 18 Nu links en rechts -7x -4x + 18 = -18 Nu links en rechts -18 -4x = -36 Nu links en rechts :-4 x = -36/-4 = 9 d. -2(4 - x) + 1 = 9x Nu haakjes wegwerken: -8 + 2x + 1 = 9x Nu links en rechts -9x -8 - 7x + 1 = 0 -7x - 7 = 0 Nu links en rechts +7 -7x = 7 Nu links en rechts :-7 x = 7/-7 = -1 |
e. 6x - 3 + 2x = 21 8x - 3 = 21 Nu links en rechts +3 8x = 24 Nu links en rechts :8 x = 24/8 = 3 f. -3(a - 2) = 2(a + 8,5) Nu haakjes wegwerken: -3a + 6 = 2a + 17 Nu links en rechts -2a -5a + 6 = 17 Nu links en rechts -6 -5a = 11 Nu links en rechts :-5 a = 11/-5 = -2 1/5 g. 5y + 3 = 3(y + 1) Nu haakjes wegwerken: 5y + 3 = 3y + 3 Nu links en rechts -3y 2y + 3 = 3 Nu links en rechts -3 2y = 0 Nu links en rechts :2 y = 0/2 = 0 h. 4 - (p + 7) = 2 Nu haakjes wegwerken: 4 - p - 7 = 2 -p - 3 = 2 Nu links en rechts +3 -p = 5 Nu links en rechts :-1 p = 5/-1 = -5 |
72.
Tip:
a(b + c) = ab + ac
(a + b)(c + d) = ac + ad + bc + bd
-(a - 1) = -a + 1, er staat een verborgen -1
a(b + c) = ab + ac
(a + b)(c + d) = ac + ad + bc + bd
-(a - 1) = -a + 1, er staat een verborgen -1
|
a. 5(x - 1) - 3x = 3(x - 5) Nu haakjes wegwerken: 5x - 5 - 3x = 3x - 15 2x - 5 = 3x - 15 Nu links en rechts -3x -x - 5 = -15 Nu links en rechts +5 -x = -10 Nu links en rechts :-1 x = -10/-1 = 10 b. 7 - 2(5 - x) = 5x Nu haakjes wegwerken: 7 - 10 + 2x = 5x -3 + 2x = 5x Nu links en rechts -5x -3 - 3x = 0 Nu links en rechts +3 -3x = 3 Nu links en rechts :-3 x = 3/-3 = -1 c. 3x + 2(x - 1) = 16 - 4x Nu haakjes wegwerken: 3x + 2x - 2 = 16 - 4x 5x - 2 = 16 - 4x Nu links en rechts +4x 9x - 2 = 16 Nu links en rechts +2 9x = 18 Nu links en rechts :9 x = 18/9 = 2 d. 4(2a - 1) - (3a - 1) = -3 Nu haakjes wegwerken: 8a - 4 - 3a + 1 = -3 5a - 3 = -3 Nu links en rechts +3 5a = 0 Nu links en rechts :5 a = 0/5 = 0 |
e. 12 - 3(5 - 4x) = 14x - 7 Nu haakjes wegwerken: 12 - 15 + 12x = 14x - 7 -3 + 12x = 14x - 7 Nu links en rechts -14x -3 - 2x = -7 Nu links en rechts +3 -2x = -4 Nu links en rechts :-2 x = -4/-2 = 2 f. 9(4 - 6x) = -22 - 4(2 - 3x) Nu haakjes wegwerken: 36 - 54x = -22 - 8 + 12x 36 - 54x = -30 + 12x Nu links en rechts -12x 36 - 66x = -30 Nu links en rechts -36 -66x = -66 Nu links en rechts :-66 x = -66/-66 = 1 g. 15(a - 2) - 5(3 - a) = 7(2 - 3a) Nu haakjes wegwerken: 15a - 30 - 15 + 5a = 14 - 21a 20a - 45 = 14 - 21a Nu links en rechts +21a 41a - 45 = 14 Nu links en rechts +45 41a = 59 Nu links en rechts :41 a = 59/41 = 1 18/41 h. (x - 3)(x + 2) + 5 = x(x - 4) + 11 Nu haakjes wegwerken: x2 + 2x - 3x - 6 + 5 = x2 - 4x + 11 x2 - x - 1 = x2 - 4x + 11 Nu links en rechts -x2 -x - 1 = -4x + 11 Nu links en rechts +4x 3x - 1 = 11 Nu links en rechts +1 3x = 12 Nu links en rechts :3 x = 12/3 = 4 |
73.
*
74.
Tip:
Delen door een breuk is hetzelfde als vermenigvuldigen met het omgekeerde.
a. Delen door een breuk is hetzelfde als vermenigvuldigen met het omgekeerde.
2/5 x = 6
Nu links en rechts :2/5
x = 6 / (2/5)
x = 6 * (5/2)
x = 30/2
x = 15
b.
2/5 x = 6
Nu links en rechts *5 (keer 5)
5 ⋅ 2/5 x = 5 ⋅ 6
10/5 x = 30
2x = 30
Nu links en rechts :2
x = 30/2 = 15
75.
Tip:
Werk eerst de breuken weg door links en rechts met hetzelfde getal te vermenigvuldigen.
Werk eerst de breuken weg door links en rechts met hetzelfde getal te vermenigvuldigen.
|
a. 1/3 x = 5 Nu links en rechts *3 (keer 3) 3 ⋅ 1/3 x = 3 ⋅ 5 x = 15 b. 3/5 x = -9 Nu links en rechts *5 (keer 5) 5 ⋅ 3/5 x = 5 ⋅ -9 15/5 x = -45 3x = -45 Nu links en rechts :3 x = -45/3 = -15 c. 1/4 x + 6 = 15 Nu links en rechts -6 1/4 x = 9 Nu links en rechts *4 (keer 4) 4 ⋅ 1/4 x = 4 ⋅ 9 x = 36 d. 2/3 x = 5 Nu links en rechts *3 (keer 3) 3 ⋅ 2/3 x = 3 ⋅ 5 2x = 15 Nu links en rechts :2 x = 15/2 = 7½ e. x - 1/3x = 4 2/3x = 4 Nu links en rechts *3 (keer 3) 3 ⋅ 2/3 x = 3 ⋅ 4 2x = 12 Nu links en rechts :2 x = 12/2 = 6 |
f. 2x + ½ = 5 Nu links en rechts -½ 2x = 4½ Nu links en rechts *2 (keer 2) 2 ⋅ 2x = 2 ⋅ 4½ 4x = 9 Nu links en rechts :4 x = 9/4 = 2¼ g. 1/6 x = 6 Nu links en rechts *6 (keer 6) 6 ⋅ 1/6 x = 6 ⋅ 6 x = 36 h. 1/3 x + 7 = 4 Nu links en rechts -7 1/3 x = -3 Nu links en rechts *3 (keer 3) 3 ⋅ 1/3 x = -9 x = -9 i. 1/2 x + 4x = -9 4½x = -9 Nu links en rechts *2 (keer 2) 2 ⋅ 4½x = 2 ⋅ -9 9x = -18 Nu links en rechts :9 x = -18/9 = -2 |
76.
Tip:
Werk eerst de breuken weg door links en rechts met hetzelfde getal te vermenigvuldigen.
Werk eerst de breuken weg door links en rechts met hetzelfde getal te vermenigvuldigen.
|
a. 1/3x + 1 = 5 Nu links en rechts -1 1/3x = 4 Nu links en rechts x3 3⋅1/3x = 3⋅4 x = 12 b. 2/3x - 2 = 6 Nu links en rechts +2 2/3x = 8 Nu links en rechts x3 3⋅2/3x = 3⋅8 2x = 24 Nu links en rechts :2 x = 24/2 = 12 c. 1/2 + x = -7 Nu links en rechts -1/2 x = -7½ |
d. 1½x + 21 = 0 Nu links en rechts -21 1½x = -21 Nu links en rechts x2 2⋅1½x = 2⋅-21 3x = -42 Nu links en rechts :3 x = -42/3 = -14 e. 1/5x - 6 = -3 Nu links en rechts +6 1/5x = 3 Nu links en rechts x5 5⋅1/5x = 5⋅3 x = 15 f. 3/7x - 2 = 4 Nu links en rechts +2 3/7x = 6 Nu links en rechts x7 7⋅3/7x = 7⋅6 21/7x = 42 3x = 42 Nu links en rechts :3 x = 42/3 = 14 |
77.
Zie afbeelding

78.
Tip:
Werk eerst de breuken weg door links en rechts met hetzelfde getal te vermenigvuldigen.
a(b + c) = ab + ac
Werk eerst de breuken weg door links en rechts met hetzelfde getal te vermenigvuldigen.
a(b + c) = ab + ac
|
a. ¼x - 2 = ½x + 6 Nu links en rechts *4 (keer 4) 4(¼x - 2) = 4(½x + 6) x - 8 = 2x + 24 Nu links en rechts -2x -x - 8 = 24 Nu links en rechts +8 -x = 32 Nu links en rechts :-1 x = 32/-1 = -32 b. ¼x - 2 = 1/3x + 6 Nu links en rechts *12 (keer 12) 12(¼x - 2) = 12(1/3x + 6) 3x - 24 = 4x + 72 Nu links en rechts -4x -x - 24 = 72 Nu links en rechts +24 -x = 96 Nu links en rechts :-1 x = 96/-1 = -96 |
c. ½x = 2/3x + 4 Nu links en rechts *6 (keer 6) 6⋅½x = 6(2/3x + 4) 3x = 4x + 24 Nu links en rechts -4x -x = 24 Nu links en rechts :-1 x = 24/-1 = -24 d. 1/3x + 6 = 2 1/6 1/3x + 6 = 13/6 Nu links en rechts *6 (keer 6) 6(1/3x + 6) = 6⋅13/6 2x + 36 = 13 Nu links en rechts -36 2x = -23 Nu links en rechts :2 x = -23/2 = -11½ |
79.
Tip:
Werk eerst de breuken weg door links en rechts met hetzelfde getal te vermenigvuldigen.
Werk eerst de breuken weg door links en rechts met hetzelfde getal te vermenigvuldigen.
|
a. 1/2x - 1/3 = 1/3(x - 2) 1/2x - 1/3 = 1/3x - 2/3 Nu links en rechts *6 (keer 6) 6(1/2x - 1/3) = 6(1/3x - 2/3) 3x - 2 = 2x - 4 Nu links en rechts -2x x - 2 = -4 Nu links en rechts +2 x = -2 b. 1 1/3x - 1/2x = 1/6(x - 12) 4/3x - 1/2x = 1/6x - 2 Nu links en rechts *6 (keer 6) 8x - 3x = x - 12 5x = x - 12 Nu links en rechts -x 4x = -12 Nu links en rechts :4 x = -12/4 = -3 c. 1/3(x - 1) = 1/4(x - 2) Nu links en rechts *12 (keer 12) 4(x - 1) = 3(x - 2) 4x - 4 = 3x - 6 Nu links en rechts -3x x - 4 = -6 Nu links en rechts +4 x = -2 d. 2 - 1/3(x - 1) = 1/4x - 2 2 - 1/3x + 1/3 = 1/4x - 2 Nu links en rechts *12 (keer 12) 24 - 4x + 4 = 3x - 24 28 - 4x = 3x - 24 Nu links en rechts -3x 28 - 7x = -24 Nu links en rechts -28 -7x = -52 Nu links en rechts :-7 x = -52/-7 = 7 3/7 |
e. 1/7x - 1/5 = 1 Nu links en rechts +1/5 1/7x = 1 1/5 1/7x = 6/5 Nu links en rechts *35 (keer 35) 5x = 42 Nu links en rechts :5 x = 42/5 = 8 2/5 f. 1/5x - 7 = 1/4(x + 2) 1/5x - 7 = 1/4x + 1/2 Nu links en rechts *20 (keer 20) 20(1/5x - 7) = 20(1/4x + 1/2) 4x - 140 = 5x + 10 Nu links en rechts -5x -x - 140 = 10 Nu links en rechts +140 -x = 150 Nu links en rechts :-1 x = 150/-1 = -150 g. 2/3(1 - x) = 3/4(x - 3) Nu links en rechts *12 (keer 12) 8(1 - x) = 9(x - 3) 8 - 8x = 9x - 27 Nu links en rechts -9x 8 - 17x = -27 Nu links en rechts -8 -17x = -35 Nu links en rechts :-17 x = -35/-17 = 2 1/17 h. 3/4(1/5x + 7) + 1 = 0 3/20x + 21/4 + 1 = 0 Nu links en rechts *20 (keer 20) 3x + 105 + 20 = 0 3x + 125 = 0 Nu links en rechts -125 3x = -125 Nu links en rechts :3 x = -125/3 = -41 2/3 |
Andere paragrafen:
3.1. Lineaire formules (1 t/m 12)
3.2. Lineaire formule opstellen (13 t/m 31)
3.3. Som- en verschilgrafieken (32 t/m 42)
3.4. De balansmethode (43 t/m 59)
3.5. Vergelijkingen oplossen (60 t/m 79)
3.1. Lineaire formules (1 t/m 12)
3.2. Lineaire formule opstellen (13 t/m 31)
3.3. Som- en verschilgrafieken (32 t/m 42)
3.4. De balansmethode (43 t/m 59)
3.5. Vergelijkingen oplossen (60 t/m 79)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


