TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 4.4 De stelling van Pythagoras toepassen HAVO/VWO 2
Boek: Getal & Ruimte - De stelling van Pythagoras HAVO/VWO 2 (deel 1) opgaven 44 t/m 56, 2013, 10e editie
44.
De volgende stellingen zijn waar: Stelling c. en Stelling d.
45.
AD2 + CD2 = AC2
62 + CD2 = 102
36 + CD2 = 100
CD2 = 100 - 36
CD2 = 64
CD = √64
CD = 8 cm
b.
opp(ABC) = 1/2 x basis x hoogte
opp(ABC) = 1/2 x AB x CD
opp(ABC) = 1/2 x 12 x 8
opp(ABC) = 48 cm2
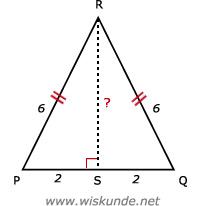
46.
22 + RS2 = 62
4 + RS2 = 36
RS2 = 36 - 4
RS2 = 32
RS = √32
RS ≈ 5,7
Dus de hoogte RS is 5,7 cm.
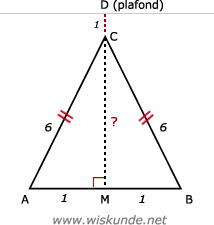
47.
12 + CM2 = 62
1 + CM2 = 36
CM2 = 36 - 1
CM2 = 35
CM = √35
CM ≈ 5,92 meter
Dus hoogte aula is 5,92 m + 1 m = 6,92 meter.
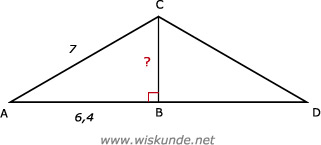
48.
6,42 + BC2 = 72
BC2 = 8,04
BC = √8,04
BC ≈ 2,84 m
Hoogte kas is dus: 3,2m + 2,84m = 6,04 meter.
En dat is 604 cm.
49.
62 + 82 = BC2
BC2 = 36 + 64
BC2 = 100
BC = √100
BC = 10
Lengte van het hek wordt: AB + BC + CD + AD
= 15 + 10 + 9 + 8
= 42 (meter)
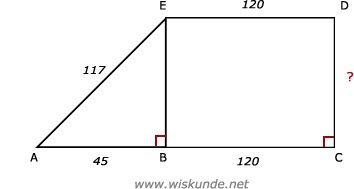
50.
AB2 + BE2 = AE2
452 + BE2 = 1172
BE2 = 1172 - 452
BE2 = 11664
BE = √11664
BE = 108
Dus CD = BE = 108 meter.
b.
Afstand parcours: 165 + 108 + 120 + 117 = 510 meter.
Ze loopt 8 rondjes: 8 x 510 = 4080 meter.
27 minuten en 40 sec. = 1660 seconden.
Dus ze loopt 4080 meter in 1660 sec.
Dat is dus: 4080 / 1660 ≈ 2,4578 m/s
Dit maal 3,6 levert: 2,4578 x 3,6 = 8,8 km/uur
51.
4,22 + 0,62 = BC2
BC2 = 18
BC = √18
BC ≈ 4,24 meter
Lengte lat = 4,24 + 0,25 + 0,25 = 4,74 meter.
52.
AC2 + 7,52 = 7,62
AC2 = 1,51
AC = √1,51
AC ≈ 1,23 meter
h = 8,7 - 0,9 - AC
h = 8,7 - 0,9 - 1,23
h = 6,57 meter
Dus de wagen kan er onder door! Je houdt 7 cm ruimte over.
53.
12 + BC2 = 1,22
1 + BC2 = 1,44
BC2 = 1,44 - 1
BC2 = 0,44
BC = √0,44
BC ≈ 0,66 meter
Dus de afmetingen van rechthoek ABCD is 1 meter bij 0,66 meter.
Inhoud van de gevraagde balk wordt dan:
lengte x breedte x hoogte = 1 x 0,66 x 10 = 6,6 m3 hout.
De volgende stellingen zijn waar: Stelling c. en Stelling d.
45.
Tip:
- oppervlakte driehoek = 1/2 x basis x hoogte
- driehoek ABC is een gelijkbenige driehoek met AC = BC = 10
- CD is de symmetrieas
- AD = 1/2 x AB
a.- oppervlakte driehoek = 1/2 x basis x hoogte
- driehoek ABC is een gelijkbenige driehoek met AC = BC = 10
- CD is de symmetrieas
- AD = 1/2 x AB
AD2 + CD2 = AC2
62 + CD2 = 102
36 + CD2 = 100
CD2 = 100 - 36
CD2 = 64
CD = √64
CD = 8 cm
b.
opp(ABC) = 1/2 x basis x hoogte
opp(ABC) = 1/2 x AB x CD
opp(ABC) = 1/2 x 12 x 8
opp(ABC) = 48 cm2
46.
Tip:
Driehoek PQR is een gelijkbenige driehoek.
Teken de hoogtelijn RS.
PS2 + RS2 = PR2Driehoek PQR is een gelijkbenige driehoek.
Teken de hoogtelijn RS.
22 + RS2 = 62
4 + RS2 = 36
RS2 = 36 - 4
RS2 = 32
RS = √32
RS ≈ 5,7
Dus de hoogte RS is 5,7 cm.

47.
Tip:
Bereken eerst MC. Tel daar 1 meter bij op en je hebt de hoogte van de aula (DM).
In een schets hoeven de afmetingen niet precies te kloppen. Daarom is het ook een schets!
AM2 + CM2 = AC2Bereken eerst MC. Tel daar 1 meter bij op en je hebt de hoogte van de aula (DM).
In een schets hoeven de afmetingen niet precies te kloppen. Daarom is het ook een schets!
12 + CM2 = 62
1 + CM2 = 36
CM2 = 36 - 1
CM2 = 35
CM = √35
CM ≈ 5,92 meter
Dus hoogte aula is 5,92 m + 1 m = 6,92 meter.

48.
Tip:
Maak een rechthoekige driehoek ABC met zijden: AB = 6,4 en AC = 7 (langste) en hoogte BC. Deze hoogte is dan 2,84 m. Tel daar 3,2 bij op en reken dan om naar cm.
AB2 + BC2 = AC2Maak een rechthoekige driehoek ABC met zijden: AB = 6,4 en AC = 7 (langste) en hoogte BC. Deze hoogte is dan 2,84 m. Tel daar 3,2 bij op en reken dan om naar cm.
6,42 + BC2 = 72
BC2 = 8,04
BC = √8,04
BC ≈ 2,84 m
Hoogte kas is dus: 3,2m + 2,84m = 6,04 meter.
En dat is 604 cm.

49.
Tip:
Maak gebruik van een hulplijn. Trek de hoogtelijn uit C op AB. Noem snijpunt E.
Werk verder met de Pythagoras driehoek: BEC.
BE2 + CE2 = BC2Maak gebruik van een hulplijn. Trek de hoogtelijn uit C op AB. Noem snijpunt E.
Werk verder met de Pythagoras driehoek: BEC.
62 + 82 = BC2
BC2 = 36 + 64
BC2 = 100
BC = √100
BC = 10
Lengte van het hek wordt: AB + BC + CD + AD
= 15 + 10 + 9 + 8
= 42 (meter)
50.
Tip:
Trek eerst hulplijn BE.
Bereken met de Stelling van Pythagoras BE. Dan weet je ook CD.
Van m/s naar km/uur -> maal 3,6
a.Trek eerst hulplijn BE.
Bereken met de Stelling van Pythagoras BE. Dan weet je ook CD.
Van m/s naar km/uur -> maal 3,6
AB2 + BE2 = AE2
452 + BE2 = 1172
BE2 = 1172 - 452
BE2 = 11664
BE = √11664
BE = 108
Dus CD = BE = 108 meter.
b.
Afstand parcours: 165 + 108 + 120 + 117 = 510 meter.
Ze loopt 8 rondjes: 8 x 510 = 4080 meter.
27 minuten en 40 sec. = 1660 seconden.
Dus ze loopt 4080 meter in 1660 sec.
Dat is dus: 4080 / 1660 ≈ 2,4578 m/s
Dit maal 3,6 levert: 2,4578 x 3,6 = 8,8 km/uur

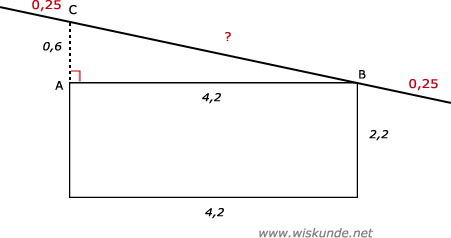
51.
Tip:
Trek de hulplijn AB.
AC = 2,8 - 2,2 = 0,6
25 cm = 0,25 m
AB2 + AC2 = BC2Trek de hulplijn AB.
AC = 2,8 - 2,2 = 0,6
25 cm = 0,25 m
4,22 + 0,62 = BC2
BC2 = 18
BC = √18
BC ≈ 4,24 meter
Lengte lat = 4,24 + 0,25 + 0,25 = 4,74 meter.

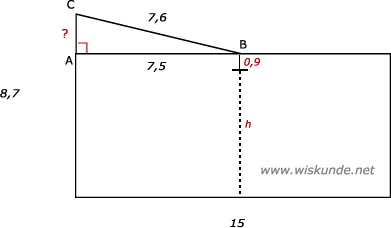
52.
Tip:
Bereken eerst AC.
Dan h = 8,7 - 0,9 - AC
AC2 + AB2 = BC2Bereken eerst AC.
Dan h = 8,7 - 0,9 - AC
AC2 + 7,52 = 7,62
AC2 = 1,51
AC = √1,51
AC ≈ 1,23 meter
h = 8,7 - 0,9 - AC
h = 8,7 - 0,9 - 1,23
h = 6,57 meter
Dus de wagen kan er onder door! Je houdt 7 cm ruimte over.

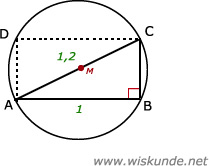
53.
Tip:
Maak een Pythagoras driehoek met schuine zijde AC 1,2 m (door middelpunt M) en een rechthoekszijde AB van 1 m.
AB is dus de breedte van de balk. ABCD is het vooraanzicht van de balk.
AB2 + BC2 = AC2Maak een Pythagoras driehoek met schuine zijde AC 1,2 m (door middelpunt M) en een rechthoekszijde AB van 1 m.
AB is dus de breedte van de balk. ABCD is het vooraanzicht van de balk.
12 + BC2 = 1,22
1 + BC2 = 1,44
BC2 = 1,44 - 1
BC2 = 0,44
BC = √0,44
BC ≈ 0,66 meter
Dus de afmetingen van rechthoek ABCD is 1 meter bij 0,66 meter.
Inhoud van de gevraagde balk wordt dan:
lengte x breedte x hoogte = 1 x 0,66 x 10 = 6,6 m3 hout.

54.
b. Lengte van de onbekende zijde: √696 ≈ 26 m
c. Lengte van de onbekende zijde: √369 ≈ 19 m
55.
32 + BC2 = 42
BC2 = 16 - 9
BC2 = 7
BC = √7
BC ≈ 2,6 meter
Dus de maximale hoogte van de camper (bij BC) is 2,6 meter.
56.
*
Tip:
Trek hulplijnen om zo een Pythagoras driehoek te maken. Soms is er meer dan 1 hulplijn nodig.
a. Lengte van de onbekende zijde: √949 ≈ 31 mTrek hulplijnen om zo een Pythagoras driehoek te maken. Soms is er meer dan 1 hulplijn nodig.
b. Lengte van de onbekende zijde: √696 ≈ 26 m
c. Lengte van de onbekende zijde: √369 ≈ 19 m
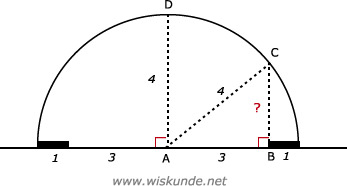
55.
Tip:
Maak een goede schets met AB = 3. AB is de maximale breedte van de rechter weghelft.
AC is 1/2 x diameter
AD = AC = 4 is de straal van de cirkel
Bereken hoogte BC in driehoek ABC
AB2 + BC2 = AC2Maak een goede schets met AB = 3. AB is de maximale breedte van de rechter weghelft.
AC is 1/2 x diameter
AD = AC = 4 is de straal van de cirkel
Bereken hoogte BC in driehoek ABC
32 + BC2 = 42
BC2 = 16 - 9
BC2 = 7
BC = √7
BC ≈ 2,6 meter
Dus de maximale hoogte van de camper (bij BC) is 2,6 meter.

56.
*
Andere paragrafen:
4.1. Wortels (1 t/m 15)
4.2. Rechthoekige driehoeken (16 t/m 23)
4.3. Zijden berekenen in rechthoekige driehoeken (24 t/m 43)
4.4. De stelling van Pythagoras toepassen (44 t/m 56)
4.5. Doorsneden (57 t/m 65)
4.6. Pythagoras in de ruimte (66 t/m 75)
4.1. Wortels (1 t/m 15)
4.2. Rechthoekige driehoeken (16 t/m 23)
4.3. Zijden berekenen in rechthoekige driehoeken (24 t/m 43)
4.4. De stelling van Pythagoras toepassen (44 t/m 56)
4.5. Doorsneden (57 t/m 65)
4.6. Pythagoras in de ruimte (66 t/m 75)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


