Antwoorden 7.1 Grafieken en vergelijkingen VWO 2
Boek: Getal & Ruimte - Kwadratische vergelijkingen VWO 2 (deel 2) opgaven 1 t/m 7, 2009Bij dit soort vergelijkingen maken we vaak gebruik van een rechte lijn en een parabool.
Bijv: bij de volgende grafieken y = -¼x2 + 4 (parabool) en de lijn y = ½x + 2 zijn de oplossingen van de vergelijking
-¼x2 + 4 = ½x + 2 de x-coördinaten van de snijpunten van deze parabool en lijn.
Vraag 1
Antwoord:
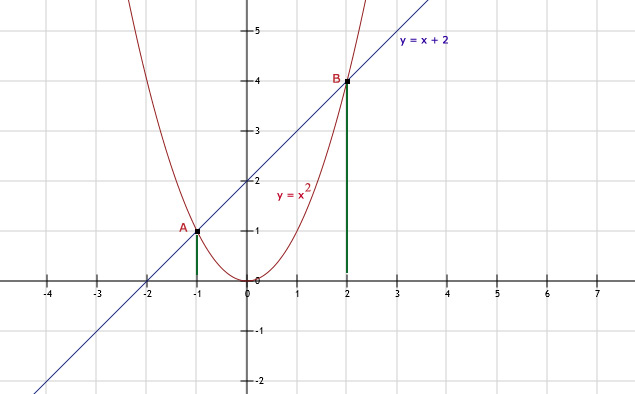
a. y = x2 is een parabool
b.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = x2 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y = x + 2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
c. De oplossingen zijn x = -1 en x = 2
d. Dat zijn de x-coördinaten van de punten A en B.
Vraag 2
Antwoord:
a. Oplossingen zijn x = 0 en x = 2
b. Oplossingen zijn x = -4 en x = 2
c. Oplossingen zijn x = -2 en x = 3
Vraag 3
Antwoord:
a. Oplossingen zijn x = -4 en x = 2
b. Oplossingen zijn x = -1 en x = 2
c. Oplossing is x = 2 (er is maar 1 snijpunt)
Vraag 4
Antwoord:
a. Oplossingen zijn x = -4 en x = 4
b. Oplossingen zijn x = -2 en x = 2
c. De parabool ligt boven de lijn en snijdt de lijn dus nooit. Dus geen snijpunten en dus geen oplossingen.
d. 2 oplossingen
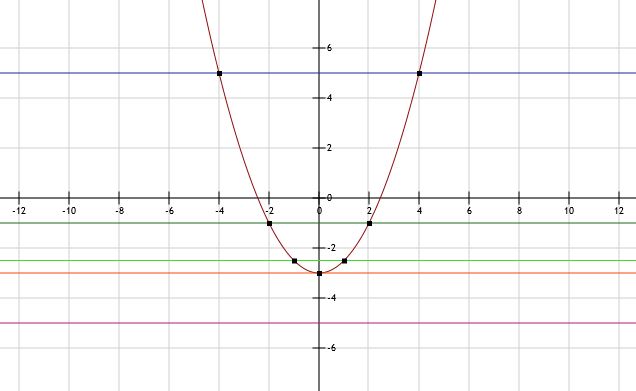
Vraag 5
Antwoord:
a. Oplossingen zijn x = -4 en x = 4 (blauw)
b. Oplossingen zijn x = -2 en x = 2 (groen)
c. Oplossing is x = 0 (oranje)
d. Geen snijpunten, dus geen oplossingen
e. Oplossingen zijn x = -1 en x = 1 (lichtgroen)
f. Geen snijpunten, dus geen oplossingen
Vraag 6
Antwoord:
a. Oplossingen zijn x = 1 en x = 3
b. Oplossingen zijn x = -1 en x = 5
c. Geen snijpunten, dus geen oplossingen
d. Geen snijpunten, dus geen oplossingen
e. Oplossingen zijn x = 1 en x = 5
f. Oplossingen x = 0
Vraag 7
Antwoord:
a. A en B zijn snijpunten van: x2 = -x + 2
b. x2 = 2x
c. 2x = -x + 2
7.1. Grafieken en vergelijkingen (1 t/m 7)
7.2. Vergelijkingen van de vorm x2 = c (8 t/m 16)
7.3. Buiten haakjes halen (17 t/m 28)
7.4. De product-som-methode (29 t/m 41)
7.5. Kwadratische vergelijkingen (42 t/m 63)
7.6. Vergelijkingen toepassen (64 t/m 69)
Word ook lid!
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


