TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 7.3 Buiten haakjes halen VWO 2
Boek: Getal & Ruimte - Kwadratische vergelijkingen VWO 2 (deel 2) opgaven 17 t/m 28, 2009Bij het ontbinden in factoren gaat het erom dat we een som als een product schrijven.
Zo kunnen we bijvoorbeeld de som x2 + 9x schrijven als het product x(x + 9).
Hierbij zijn x en (x + 9) de factoren. Je kunt nu ook zeggen dat we x voor de haakjes hebben gehaald. Probeer een zo hoog mogelijke gemeenschappelijke factor voor de haakjes te halen!
Zo kunnen we bijvoorbeeld de som x2 + 9x schrijven als het product x(x + 9).
Hierbij zijn x en (x + 9) de factoren. Je kunt nu ook zeggen dat we x voor de haakjes hebben gehaald. Probeer een zo hoog mogelijke gemeenschappelijke factor voor de haakjes te halen!
17.
b. 2 ⋅ 2 ⋅ 5 ⋅ p ⋅ q ⋅ q
c. 11 ⋅ x ⋅ y ⋅ y
d. 5 ⋅ 5 ⋅ x ⋅ x ⋅ y
e. 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ x ⋅ x ⋅ x ⋅ y ⋅ y
f. 3 ⋅ 7 ⋅ x ⋅ x ⋅ y ⋅ z ⋅ z ⋅ z
18.
a. x2 - 5x
b. 3x + 33
c. 3a2 - 2ab
d. 15a2 + 3a
e. x3 - 8x2
f. -2x2 + 14x
19.
a. 9
b. (2x + 1)
c. 1
d. (5x - 3)
20.
a. 2(2x + 3y)
b. x(4 - y)
c. x(x + 18)
d. 2(p - 3)
e. p(q + r)
f. x(x - 5)
g. x(3x + 5)
h. x(7y - 20)
i. b(8a - 3)
21.
b. 6(pq - 5p)
c. 2p(3q - 15)
d. 6p(q - 5)
22.
b. 3b(4a - 3)
c. 3a(a + 2)
d. 3(a2 - 2b)
e. 3a(b - 1)
f. 3a(b - 3c)
g. 4xy(3z - 4)
h. 2x(y + 4z)
i. 5x2(1 - 3x)
23.
a. 6x(x2 - 2)
b. 5x(5x - 6)
c. 5x2(2 + y)
d. 3x2(2x2 - 1)
e. 6abc(3a + 2b)
f. x2(x2 - x + 1)
g. x(4x + y + y2)
h. 2x5(6x3 + 9x - 8)
i. 3pq2r(3p2 - 2r2)
24.
b. 9x2 - 64
c. a2 - 1
d. a2 - b2
e. x6 - 4
f. p4 - q4
25.
a. (x + 3)(x + 3) = x2 + 3x + 3x + 9 = x2 + 6x + 9
b. Fred heeft het fout.
26.
a. (5a - 2)(5a + 2)
b. (a - 8)(a + 8)
c. a(a - 64)
d. (6a - 11)(6a + 11)
e. a(36a - 1)
f. (15a - 0,1)(15a + 0,1)
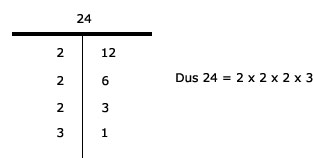
Tip:
Deel 24 door 2 en je krijgt 12. Deel 12 door 2 en je krijgt 6. Deel 6 door 2 en je krijgt 3. Deel 3 door 3 en je krijgt 1. Dus 24 is dan ontbonden in: 24 = 2 x 2 x 2 x 3. Je kunt ook een T-tabel maken.
a. 2 ⋅ 2 ⋅ 3 ⋅ p ⋅ qDeel 24 door 2 en je krijgt 12. Deel 12 door 2 en je krijgt 6. Deel 6 door 2 en je krijgt 3. Deel 3 door 3 en je krijgt 1. Dus 24 is dan ontbonden in: 24 = 2 x 2 x 2 x 3. Je kunt ook een T-tabel maken.
b. 2 ⋅ 2 ⋅ 5 ⋅ p ⋅ q ⋅ q
c. 11 ⋅ x ⋅ y ⋅ y
d. 5 ⋅ 5 ⋅ x ⋅ x ⋅ y
e. 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ x ⋅ x ⋅ x ⋅ y ⋅ y
f. 3 ⋅ 7 ⋅ x ⋅ x ⋅ y ⋅ z ⋅ z ⋅ z

18.
a. x2 - 5x
b. 3x + 33
c. 3a2 - 2ab
d. 15a2 + 3a
e. x3 - 8x2
f. -2x2 + 14x
19.
a. 9
b. (2x + 1)
c. 1
d. (5x - 3)
20.
a. 2(2x + 3y)
b. x(4 - y)
c. x(x + 18)
d. 2(p - 3)
e. p(q + r)
f. x(x - 5)
g. x(3x + 5)
h. x(7y - 20)
i. b(8a - 3)
21.
Tip:
Wat is de grootste gemeenschappelijke factor die je voor de haakjes kunt halen? Dat is 6p.
a. p(6q - 30)Wat is de grootste gemeenschappelijke factor die je voor de haakjes kunt halen? Dat is 6p.
b. 6(pq - 5p)
c. 2p(3q - 15)
d. 6p(q - 5)
22.
Tip:
Ontbind in factoren: 7x2 - 21x3
7x2 = 7 ⋅ x ⋅ x
21x3 = 3 ⋅ 7 ⋅ x ⋅ x ⋅ x
Dus gemeenschappelijke factoren zijn 7 ⋅ x ⋅ x, dus haal 7x2 voor de haakjes. Dat levert: 7x2 - 21x3 = 7x2(1 - 3x)
a. 3a(b + 3)Ontbind in factoren: 7x2 - 21x3
7x2 = 7 ⋅ x ⋅ x
21x3 = 3 ⋅ 7 ⋅ x ⋅ x ⋅ x
Dus gemeenschappelijke factoren zijn 7 ⋅ x ⋅ x, dus haal 7x2 voor de haakjes. Dat levert: 7x2 - 21x3 = 7x2(1 - 3x)
b. 3b(4a - 3)
c. 3a(a + 2)
d. 3(a2 - 2b)
e. 3a(b - 1)
f. 3a(b - 3c)
g. 4xy(3z - 4)
h. 2x(y + 4z)
i. 5x2(1 - 3x)
23.
a. 6x(x2 - 2)
b. 5x(5x - 6)
c. 5x2(2 + y)
d. 3x2(2x2 - 1)
e. 6abc(3a + 2b)
f. x2(x2 - x + 1)
g. x(4x + y + y2)
h. 2x5(6x3 + 9x - 8)
i. 3pq2r(3p2 - 2r2)
24.
Tip:
Gebruik merkwaardig product: (a - b)(a + b) = a2 - b2
a. x2 - 25Gebruik merkwaardig product: (a - b)(a + b) = a2 - b2
b. 9x2 - 64
c. a2 - 1
d. a2 - b2
e. x6 - 4
f. p4 - q4
25.
a. (x + 3)(x + 3) = x2 + 3x + 3x + 9 = x2 + 6x + 9
b. Fred heeft het fout.
26.
a. (5a - 2)(5a + 2)
b. (a - 8)(a + 8)
c. a(a - 64)
d. (6a - 11)(6a + 11)
e. a(36a - 1)
f. (15a - 0,1)(15a + 0,1)
27.
b. x2(x - 64)
c. x(x - 8)(x + 8)
d. x2(x - 4)(x + 4)
e. x2(x2 + 16)
f. x3(x + 16)
28.
b. (x - 2)(x + 2)(x2 + 4)
c. (a5 - 3)(a5 + 3)
d. q6(q2 + p6)
e. (x4y3 - z)(x4y3 + z)
f. 18(k8 - 1) = 18(k4 - 1)(k4 + 1) =
18(k2 - 1)(k2 + 1)(k4 + 1) =
18(k - 1)(k + 1)(k2 + 1)(k4 + 1)
Tip:
x3 - 4x = x(x2 - 4) = x(x + 2)(x - 2), want x2 - 4 is weer een merkwaardig product.
a. x(x - 4)(x + 4)x3 - 4x = x(x2 - 4) = x(x + 2)(x - 2), want x2 - 4 is weer een merkwaardig product.
b. x2(x - 64)
c. x(x - 8)(x + 8)
d. x2(x - 4)(x + 4)
e. x2(x2 + 16)
f. x3(x + 16)
28.
Tip:
Bij f. kun je meerdere merkwaardige producten uitschrijven!
a. 5(p - 5)(p + 5)Bij f. kun je meerdere merkwaardige producten uitschrijven!
b. (x - 2)(x + 2)(x2 + 4)
c. (a5 - 3)(a5 + 3)
d. q6(q2 + p6)
e. (x4y3 - z)(x4y3 + z)
f. 18(k8 - 1) = 18(k4 - 1)(k4 + 1) =
18(k2 - 1)(k2 + 1)(k4 + 1) =
18(k - 1)(k + 1)(k2 + 1)(k4 + 1)
Andere paragrafen:
7.1. Grafieken en vergelijkingen (1 t/m 7)
7.2. Vergelijkingen van de vorm x2 = c (8 t/m 16)
7.3. Buiten haakjes halen (17 t/m 28)
7.4. De product-som-methode (29 t/m 41)
7.5. Kwadratische vergelijkingen (42 t/m 63)
7.6. Vergelijkingen toepassen (64 t/m 69)
7.1. Grafieken en vergelijkingen (1 t/m 7)
7.2. Vergelijkingen van de vorm x2 = c (8 t/m 16)
7.3. Buiten haakjes halen (17 t/m 28)
7.4. De product-som-methode (29 t/m 41)
7.5. Kwadratische vergelijkingen (42 t/m 63)
7.6. Vergelijkingen toepassen (64 t/m 69)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


