TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 8.1 Exponentiële groei HAVO 3
Boek: Getal & Ruimte - Allerlei verbanden HAVO 3 (deel 2) opgaven 1 t/m 17, 2010Wat is de formule voor exponentiele groei?
Formule: N = b x gt waarbij,
b is de beginwaarde of beginhoeveelheid
g is de groeifactor per tijdseenheid
Formule: N = b x gt waarbij,
b is de beginwaarde of beginhoeveelheid
g is de groeifactor per tijdseenheid
1.
a. Verkochte fotoboeken in 2009: 2 x 0,6 = 1,2 miljoen. In 2010 was dat 2 x 1,2 = 2,4 miljoen.
b.
2.
a. De beginhoeveelheid (zie de formule) is: b = 18.
De groeifactor (zie de formule) is: g = 1,3.
b. Bij t = 4 krijgen we N = 51,4
c. Probeer enkele t-waarden uit. Zie dat bij t =14 de hoeveelheid voor het eerst komt boven de 650.
3.
a. Formule: h = 1,8 x 1,2t
b. 1 maart 2014 is 6 jaar later, dus t = 6. Dit levert: h = 1,8 x 1,26 ≈ 5,37. Dus 5 meter en 37 cm.
c. Bij t = 9 dan is h = 9,3 (net niet hoog genoeg), bij t = 10 dan is h = 11,1. Dus na 10 jaar. Dat is op 1 maart 2018.
4.
a. Formule: N = 6500 x 1,06t
b. t = 10 levert: N = 11 640. Dus 11 640 werknemers op 1 jan. 2020.
c. Bij t = 19 dan is N = 19 666 (net niet genoeg), bij t = 20 dan is N = 20 846. Dus op 1 jan. 2030.
5.
a. Formule: N = 13,7 x 1,025t
b. t = 6 levert: N = 15,9. Dus 15,9 miljoen inwoners op 1 jan. 2014.
c. Bij t = 15 dan is N = 19,8 (net niet genoeg), bij t = 16 dan is N = 20,3. Dus op 1 jan. 2024.
d. t = 10 geeft N = 17,5. Dan 28% x 17,5 = 4,9 miljoen inwoners.
6.
a. Formule: N = 20 000 x 2t
b. t = 4 levert: N = 20 000 x 24 = 320 000 bacterien na 2 uur
t = 8 levert: N = 20 000 x 28 = 5 120 000 bacterien na 4 uur
c.
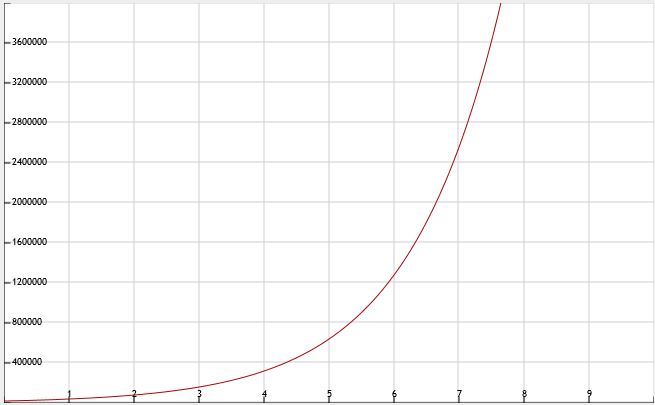
d. Zie afbeelding
7.
a. Formule: N = 1,8 x 1,08t
b. t = 5 levert: 1,8 x 1,085 = 2,6 miljard betalingen per pinpas
c. 2014: t = 6 levert: 1,8 x 1,086 = 2,86 miljard betalingen per pinpas
2015: t = 7 levert: 1,8 x 1,087 = 3,08 miljard betalingen per pinpas
Verschil = 3,08 - 2,82 = 0,2 miljard.
d. Als t = 13 geeft N ≈ 4,9 (net niet genoeg, dus), bij t = 14 krijg je N = 5,3.
8.
*
9.
a. 1280 / 1024 = 1,25, dus g = 1,25
b. N = 1024 x 1,25t
c.
d. t = 8 levert N ≈ 6103,51, dus op gehelen 6104
10.
a.
I heeft exponentiele groei, g = 1,5
II heeft geen exponentiele groei
III heeft exponentiele groei, g = 1,2
b.
I heeft formule: N = 8 x 1,5t
II heeft formule: N = 50 x 1,2t
a. Verkochte fotoboeken in 2009: 2 x 0,6 = 1,2 miljoen. In 2010 was dat 2 x 1,2 = 2,4 miljoen.
b.
| tijd t | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| N in miljoenen | 0,3 | 0,6 | 1,2 | 2,4 | 4,8 | 9,6 | 19,2 |
2.
a. De beginhoeveelheid (zie de formule) is: b = 18.
De groeifactor (zie de formule) is: g = 1,3.
b. Bij t = 4 krijgen we N = 51,4
c. Probeer enkele t-waarden uit. Zie dat bij t =14 de hoeveelheid voor het eerst komt boven de 650.
3.
a. Formule: h = 1,8 x 1,2t
b. 1 maart 2014 is 6 jaar later, dus t = 6. Dit levert: h = 1,8 x 1,26 ≈ 5,37. Dus 5 meter en 37 cm.
c. Bij t = 9 dan is h = 9,3 (net niet hoog genoeg), bij t = 10 dan is h = 11,1. Dus na 10 jaar. Dat is op 1 maart 2018.
4.
a. Formule: N = 6500 x 1,06t
b. t = 10 levert: N = 11 640. Dus 11 640 werknemers op 1 jan. 2020.
c. Bij t = 19 dan is N = 19 666 (net niet genoeg), bij t = 20 dan is N = 20 846. Dus op 1 jan. 2030.
5.
a. Formule: N = 13,7 x 1,025t
b. t = 6 levert: N = 15,9. Dus 15,9 miljoen inwoners op 1 jan. 2014.
c. Bij t = 15 dan is N = 19,8 (net niet genoeg), bij t = 16 dan is N = 20,3. Dus op 1 jan. 2024.
d. t = 10 geeft N = 17,5. Dan 28% x 17,5 = 4,9 miljoen inwoners.
6.
a. Formule: N = 20 000 x 2t
b. t = 4 levert: N = 20 000 x 24 = 320 000 bacterien na 2 uur
t = 8 levert: N = 20 000 x 28 = 5 120 000 bacterien na 4 uur
c.
| t in 1/2 uren | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| aantal N | 20.000 | 40.000 | 80.000 | 160.000 | 320.000 | 640.000 | 1.280.000 | 2.560.000 |
d. Zie afbeelding

7.
a. Formule: N = 1,8 x 1,08t
b. t = 5 levert: 1,8 x 1,085 = 2,6 miljard betalingen per pinpas
c. 2014: t = 6 levert: 1,8 x 1,086 = 2,86 miljard betalingen per pinpas
2015: t = 7 levert: 1,8 x 1,087 = 3,08 miljard betalingen per pinpas
Verschil = 3,08 - 2,82 = 0,2 miljard.
d. Als t = 13 geeft N ≈ 4,9 (net niet genoeg, dus), bij t = 14 krijg je N = 5,3.
8.
*
9.
a. 1280 / 1024 = 1,25, dus g = 1,25
b. N = 1024 x 1,25t
c.
| t-in-jaren | 0 | 1 | 2 | 3 | 4 | 5 |
| aantal N | 1024 | 1280 | 1600 | 2000 | 2500 | 3125 |
d. t = 8 levert N ≈ 6103,51, dus op gehelen 6104
10.
a.
I heeft exponentiele groei, g = 1,5
II heeft geen exponentiele groei
III heeft exponentiele groei, g = 1,2
b.
I heeft formule: N = 8 x 1,5t
II heeft formule: N = 50 x 1,2t
11.
a. 4,9 / 3,5 = 1,4 deze verhouding vind je opeenvolgend, dus exponentiele groei
b. O = 3,5 x 1,4t
c. Voor t = 8
12.
a. 87 / 66 ≈ 1,32 deze verhouding vind je opeenvolgend, dus exponentiele groei
b. N = 66 x 1,32t
c. Voor t = 7 geldt: N = 66 x 1,327 ≈ 460,85, dus afgerond 461 bevers
d. 12 x 66 = 792, dit bereik je bij t = 9 en dat is dus in 2014.
13.
a. Aantal duiven in juli 2008 = 0,5 x 0,5 x 20 000 = 5 000
b.
c. N = 20000 x 0,5t
14.
a. Groeifactor g = 0,83
b. Voor t = 4 krijgen we N ≈ 403,4
c. Voor t = 24, dan is N kleiner dan 10. Bij 23 nog net erboven (11,7).
15.
a. Na dagen: 3/4 x 3/4 x 12 = 6,75 mg over
b. N = 12 x (¾)t
c. Bij t = 12, dan is er nog 0,38 mg over
16.
a. N = 7,5 x 0,986t
b. Neem t = 4 levert ≈7,1 miljoen inwoners
c. Bij t = 11 is N ≈ 6,33, dus op 1 jan. 2019
d. 7,29 (bij t = 2) - 6,33 (bij t = 12) = 0,96 miljoen
17.
a. 901 / 1018 ≈ 0,885 deze verhouding vind je opeenvolgend, dus exponentiele groei
b. P = 1018 x 0,885h
c. Voor h = 7 geldt: P = 1018 x 0,8857≈ 432,86, dus afgerond 433
d. Berghut ligt op een hoogte beneden 4000 meter.
a. 4,9 / 3,5 = 1,4 deze verhouding vind je opeenvolgend, dus exponentiele groei
b. O = 3,5 x 1,4t
c. Voor t = 8
12.
a. 87 / 66 ≈ 1,32 deze verhouding vind je opeenvolgend, dus exponentiele groei
b. N = 66 x 1,32t
c. Voor t = 7 geldt: N = 66 x 1,327 ≈ 460,85, dus afgerond 461 bevers
d. 12 x 66 = 792, dit bereik je bij t = 9 en dat is dus in 2014.
13.
a. Aantal duiven in juli 2008 = 0,5 x 0,5 x 20 000 = 5 000
b.
| t-in-maanden | 0 | 1 | 2 | 3 | 4 | 5 |
| aantal duiven | 20.000 | 10.000 | 5.000 | 2.500 | 1.250 | 625 |
c. N = 20000 x 0,5t
14.
a. Groeifactor g = 0,83
b. Voor t = 4 krijgen we N ≈ 403,4
c. Voor t = 24, dan is N kleiner dan 10. Bij 23 nog net erboven (11,7).
15.
a. Na dagen: 3/4 x 3/4 x 12 = 6,75 mg over
b. N = 12 x (¾)t
c. Bij t = 12, dan is er nog 0,38 mg over
16.
a. N = 7,5 x 0,986t
b. Neem t = 4 levert ≈7,1 miljoen inwoners
c. Bij t = 11 is N ≈ 6,33, dus op 1 jan. 2019
d. 7,29 (bij t = 2) - 6,33 (bij t = 12) = 0,96 miljoen
17.
a. 901 / 1018 ≈ 0,885 deze verhouding vind je opeenvolgend, dus exponentiele groei
b. P = 1018 x 0,885h
c. Voor h = 7 geldt: P = 1018 x 0,8857≈ 432,86, dus afgerond 433
d. Berghut ligt op een hoogte beneden 4000 meter.
Andere paragrafen:
8.1. Exponentiële groei (1 t/m 17)
8.2. Procenten en groeifactoren (18 t/m 28)
8.3. Periodieke verbanden (29 t/m 36)
8.4. Machtsfuncties (37 t/m 45)
8.5. Vergelijkingen met machten (46 t/m 56)
8.6. Omgekeerd evenredige verbanden (57 t/m 60)
8.1. Exponentiële groei (1 t/m 17)
8.2. Procenten en groeifactoren (18 t/m 28)
8.3. Periodieke verbanden (29 t/m 36)
8.4. Machtsfuncties (37 t/m 45)
8.5. Vergelijkingen met machten (46 t/m 56)
8.6. Omgekeerd evenredige verbanden (57 t/m 60)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


