TIP: Wil je ook toegang tot meer dan 16.000 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 8.5 Vergelijkingen met machten HAVO 3
Boek: Getal & Ruimte - Allerlei verbanden HAVO 3 (deel 2) opgaven 46 t/m 56, 2010Vergelijkingen oplossen van de vorm: xn = a
Bijvoorbeeld: x6 = 64
x = 6√(64) = 2
Bijvoorbeeld: x6 = 64
x = 6√(64) = 2
46.
a. Inhoud kubus = ribbe3 = 43 = 64
b. 23 = 8 dus ribbe = 2
c. De ribben moeten langer zijn dan 3 cm.
47.
a. De grafiek van x4 snijdt de horizontale lijn y = 100 in 2 punten. Dus er zijn 2 oplossingen.
b. y = x6 ligt boven de x-as en y = -20 is een horizontale lijn onder de x-as. Dus deze 2 snijden elkaar nooit.
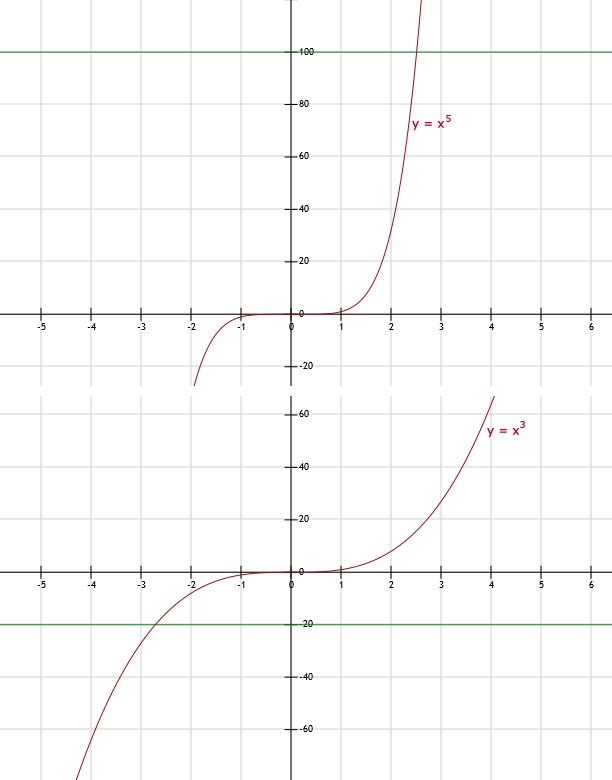
c. (zie afbeelding) y = x5 snijdt de lijn y = 100 in 1 punt, dus 1 oplossing.
y = x3 snijdt de lijn y = -20 in 1 punt, dus 1 oplossing.
48.
a. x = 5√17 ≈ 1,8
b. x = 4√28 ≈ 2,3 v x = -4√28 ≈ -2,3
c. x = 7√100 ≈ 1,9
d. x = 3√-21 ≈ -2,8
e. Geen oplossingen
f. x = 5√-0,01 ≈ -0,4
g. x = 6√7 ≈ 1,4 v x = -6√7 ≈ -1,4
h. x = 10√99999 ≈ 3,2 v x = -10√99999 ≈ -3,2
i. x = 6√666 ≈ 3,0 v x = -6√666 ≈ -3,0
49.
r3 = 500
r = 3 √500 ≈ 7,94 dm. Dat is 79,4 cm.
50.
a. x = 6√(50 / 3) ≈ 1,60 v x = -6√(50 / 3) ≈ -1,60
b. x = 3√44 ≈ 3,53
c. x = 7√-27 ≈ -1,60
d. x = 4√(176 / 5) ≈ 2,44 v x = -4√(176 / 5) ≈ -2,44
e. Geen oplossingen
f. x = 5√(221 / 0,3) ≈ 3,75
51.
a. x = 4√(520 / 6) ≈ 3,05 v x = -4√(520 / 6) ≈ -3,05
b. x = 5√ (-992 / 3) ≈ -3,19
c. x = 10√30 ≈ 1,41 v x = -10√30 ≈ -1,41
d. x = 3√-11 ≈ -2,22
e. x = 6√9819 ≈ 4,63 v x = -6√9819 ≈ -4,63
f. x = 3√(9 / 4) ≈ 1,31
52.
a. L = 8, geeft G = 0,45 x 83 = 230,4 gram
b. L = 3√ (350 / 0,45) ≈ 9,2 dm. Dus 92 cm.
53.
a. y = 90x2
b. y = x3
c. Voor x = 0 en x = 90
54.
a. x2(0,2x - 100) = 0 levert x = 0 v x = 100/0,2 = 500
b. x6(0,1x2 - 20) = 0 levert x = 0 v x ≈ 14,1 v x ≈ -14,1
c. a2(0,25a - 1) = 0 levert a = 0 v a = 1/0,25 = 4
d. p(0,3p3 - 3000) = 0 levert p = 0 v p = 3√10 000 ≈ 21,5
55.
a. p3(8 - p5) = 0 levert p = 0 v p = 5√8 ≈ 1,5
b. p2(2 - p6) = 0 levert p = 0 v p ≈ 1,1 v p ≈ -1,1
c. 3x3(2 + x3) = 0 levert x = 0 v x = 3√-2 ≈ -1,3
d. 3x3(x4 - 4) = 0 levert x = 0 v x ≈ 1,4 v x ≈ -1,4
a. Inhoud kubus = ribbe3 = 43 = 64
b. 23 = 8 dus ribbe = 2
c. De ribben moeten langer zijn dan 3 cm.
47.
a. De grafiek van x4 snijdt de horizontale lijn y = 100 in 2 punten. Dus er zijn 2 oplossingen.
b. y = x6 ligt boven de x-as en y = -20 is een horizontale lijn onder de x-as. Dus deze 2 snijden elkaar nooit.
c. (zie afbeelding) y = x5 snijdt de lijn y = 100 in 1 punt, dus 1 oplossing.
y = x3 snijdt de lijn y = -20 in 1 punt, dus 1 oplossing.

48.
a. x = 5√17 ≈ 1,8
b. x = 4√28 ≈ 2,3 v x = -4√28 ≈ -2,3
c. x = 7√100 ≈ 1,9
d. x = 3√-21 ≈ -2,8
e. Geen oplossingen
f. x = 5√-0,01 ≈ -0,4
g. x = 6√7 ≈ 1,4 v x = -6√7 ≈ -1,4
h. x = 10√99999 ≈ 3,2 v x = -10√99999 ≈ -3,2
i. x = 6√666 ≈ 3,0 v x = -6√666 ≈ -3,0
49.
r3 = 500
r = 3 √500 ≈ 7,94 dm. Dat is 79,4 cm.
50.
a. x = 6√(50 / 3) ≈ 1,60 v x = -6√(50 / 3) ≈ -1,60
b. x = 3√44 ≈ 3,53
c. x = 7√-27 ≈ -1,60
d. x = 4√(176 / 5) ≈ 2,44 v x = -4√(176 / 5) ≈ -2,44
e. Geen oplossingen
f. x = 5√(221 / 0,3) ≈ 3,75
51.
a. x = 4√(520 / 6) ≈ 3,05 v x = -4√(520 / 6) ≈ -3,05
b. x = 5√ (-992 / 3) ≈ -3,19
c. x = 10√30 ≈ 1,41 v x = -10√30 ≈ -1,41
d. x = 3√-11 ≈ -2,22
e. x = 6√9819 ≈ 4,63 v x = -6√9819 ≈ -4,63
f. x = 3√(9 / 4) ≈ 1,31
52.
a. L = 8, geeft G = 0,45 x 83 = 230,4 gram
b. L = 3√ (350 / 0,45) ≈ 9,2 dm. Dus 92 cm.
53.
a. y = 90x2
b. y = x3
c. Voor x = 0 en x = 90
54.
a. x2(0,2x - 100) = 0 levert x = 0 v x = 100/0,2 = 500
b. x6(0,1x2 - 20) = 0 levert x = 0 v x ≈ 14,1 v x ≈ -14,1
c. a2(0,25a - 1) = 0 levert a = 0 v a = 1/0,25 = 4
d. p(0,3p3 - 3000) = 0 levert p = 0 v p = 3√10 000 ≈ 21,5
55.
a. p3(8 - p5) = 0 levert p = 0 v p = 5√8 ≈ 1,5
b. p2(2 - p6) = 0 levert p = 0 v p ≈ 1,1 v p ≈ -1,1
c. 3x3(2 + x3) = 0 levert x = 0 v x = 3√-2 ≈ -1,3
d. 3x3(x4 - 4) = 0 levert x = 0 v x ≈ 1,4 v x ≈ -1,4
56.
f(x) = g(x) levert:
0,2x4 = 0,01x6
x4(0,2 - 0,01x2) = 0
x = 0 v x ≈ 4,47 v x ≈ -4,47
Snijpunten (4,47 ; 79,8) en (-4,47 ; 79,8)
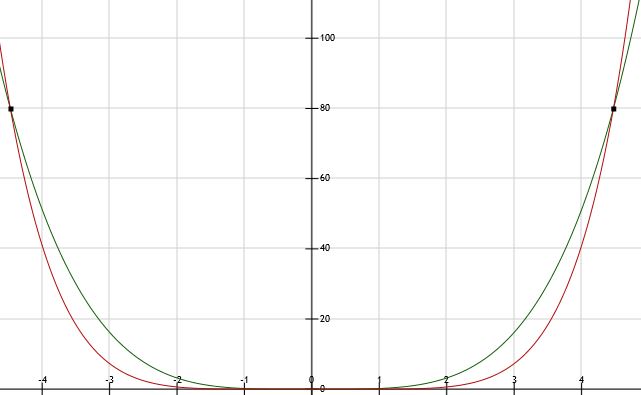
f(x) = g(x) levert:
0,2x4 = 0,01x6
x4(0,2 - 0,01x2) = 0
x = 0 v x ≈ 4,47 v x ≈ -4,47
Snijpunten (4,47 ; 79,8) en (-4,47 ; 79,8)

Andere paragrafen:
8.1. Exponentiële groei (1 t/m 17)
8.2. Procenten en groeifactoren (18 t/m 28)
8.3. Periodieke verbanden (29 t/m 36)
8.4. Machtsfuncties (37 t/m 45)
8.5. Vergelijkingen met machten (46 t/m 56)
8.6. Omgekeerd evenredige verbanden (57 t/m 60)
8.1. Exponentiële groei (1 t/m 17)
8.2. Procenten en groeifactoren (18 t/m 28)
8.3. Periodieke verbanden (29 t/m 36)
8.4. Machtsfuncties (37 t/m 45)
8.5. Vergelijkingen met machten (46 t/m 56)
8.6. Omgekeerd evenredige verbanden (57 t/m 60)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2025)


