TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 2.1 Hoeken berekenen in vlakke figuren VMBO 4 KGT
Boek: Getal & Ruimte - Hoeken en afstanden VMBO 4 (deel 1) opgaven 1 t/m 24, 2011De som van de hoeken in een driehoek is gelijk aan 180º.
In een gelijkzijdige driehoek zijn alle zijden gelijk en zijn alle hoeken gelijk aan 180º / 3 = 60º.
In een gelijkbenige driehoek zijn de 2 basishoeken gelijk.
Een rechthoekige driehoek is een driehoek met een hoek van 90º.
Een lijn die een hoek in 2 gelijke stukken verdeelt, noemen we de bissectrice of de deellijn.
In een gelijkzijdige driehoek zijn alle zijden gelijk en zijn alle hoeken gelijk aan 180º / 3 = 60º.
In een gelijkbenige driehoek zijn de 2 basishoeken gelijk.
Een rechthoekige driehoek is een driehoek met een hoek van 90º.
Een lijn die een hoek in 2 gelijke stukken verdeelt, noemen we de bissectrice of de deellijn.
1.
b. Door de rode balletjes. CD is de deellijn of bissectrice.
c. ∠C12 = 2 x 34º = 68º
d. ∠B = 180º - ∠A - ∠C12 = 180º - 43º - 68º = 69º
e. ∠D2 = 180º - 103º = 77º
2.
b. SU en TU zijn even lang. Dus SU = TU.
c. ∠U = 180º - 72º - 72º = 36º
3.
b. ∠A2 = 180º - 60º = 120º (samen een gestrekte hoek)
c. ∠D = 180º - 20º - 120º = 40º (hoekensom driehoek 180º)
4.
∠N2 = 180º - 76º = 104º (samen een gestrekte hoek)
∠K2 = 180º - 53º - 104º = 23º (hoekensom driehoek 180º)
5.
b. ∠PTS = 180º - 90º - 60º = 30º
c. ∠STQ = 180º - (andere hoeken bij T) = 180º - 90º - 30º = 60º
6.
∠B2 = 180º - 36º - 42º = 102º (hoekensom driehoek 180º)
∠B1 = 180º - 102º = 78º (samen een gestrekte hoek)
∠B1 = ∠A = 78º
∠D2 = 180º - ∠B1 - ∠A = 180º - 78º - 78º = 24º
7.
∠B2 = ∠B1 = 64º (overstaande hoeken)
Omdat hoek ∠B2 = 64º, is er voor de hoeken D en E nog maar 116º over.
∠E = ∠D = 116º / 2 = 58º
8.
b. ∠E2 = 180º - 22º - 22º = 136º (hoekensom driehoek 180º)
∠E1 = 180º - 136º = 44º (samen een gestrekte hoek)
c. ∠A1 = 180º - ∠D - ∠E1 = 180º - 90º - 44º = 46º
9.
Antwoord: draaisymmetrie
10.
a. Succes!
b. Ja
c. Ja
d. Zie afbeelding
e. *
Tip:
Om een hoek te berekenen in een driehoek doe je 180º minus de andere hoeken die bekend zijn.
a. ∠C1 = 180º - 103º - 43º = 34ºOm een hoek te berekenen in een driehoek doe je 180º minus de andere hoeken die bekend zijn.
b. Door de rode balletjes. CD is de deellijn of bissectrice.
c. ∠C12 = 2 x 34º = 68º
d. ∠B = 180º - ∠A - ∠C12 = 180º - 43º - 68º = 69º
e. ∠D2 = 180º - 103º = 77º
2.
Tip:
In een gelijkbenige driehoek zijn de 2 basishoeken gelijk. Dus ∠S = ∠T = 72º.
a. Driehoek STU is een gelijkbenige driehoek. Dat zie je aan de streepjes.In een gelijkbenige driehoek zijn de 2 basishoeken gelijk. Dus ∠S = ∠T = 72º.
b. SU en TU zijn even lang. Dus SU = TU.
c. ∠U = 180º - 72º - 72º = 36º
3.
Tip:
Omdat driehoek ABC gelijkzijdig is geldt: ∠A1 = ∠B = ∠C1 = 60º
a. Driehoek ABC is een gelijkzijdige driehoek. Dat zie je aan de streepjes (3x).Omdat driehoek ABC gelijkzijdig is geldt: ∠A1 = ∠B = ∠C1 = 60º
b. ∠A2 = 180º - 60º = 120º (samen een gestrekte hoek)
c. ∠D = 180º - 20º - 120º = 40º (hoekensom driehoek 180º)
4.
Tip:
Teken het plaatje over op een kladblaadje en zet daarbij de hoeken die je steeds berekent erbij. Dan wordt het steeds duidelijker!
∠K1 = 180º - 76º - 54º = 50º (hoekensom driehoek 180º)Teken het plaatje over op een kladblaadje en zet daarbij de hoeken die je steeds berekent erbij. Dan wordt het steeds duidelijker!
∠N2 = 180º - 76º = 104º (samen een gestrekte hoek)
∠K2 = 180º - 53º - 104º = 23º (hoekensom driehoek 180º)
5.
Tip:
Driehoek PQR is gelijkzijdig. Dus: ∠P = ∠Q = ∠R = 60º.
a. ∠RQT = 180º - 90º - 60º = 30ºDriehoek PQR is gelijkzijdig. Dus: ∠P = ∠Q = ∠R = 60º.
b. ∠PTS = 180º - 90º - 60º = 30º
c. ∠STQ = 180º - (andere hoeken bij T) = 180º - 90º - 30º = 60º
6.
∠B2 = 180º - 36º - 42º = 102º (hoekensom driehoek 180º)
∠B1 = 180º - 102º = 78º (samen een gestrekte hoek)
∠B1 = ∠A = 78º
∠D2 = 180º - ∠B1 - ∠A = 180º - 78º - 78º = 24º
7.
Tip:
De hoeken D en E zijn de gelijke basishoeken van de gelijkbenige driehoek BED.
∠B1 = 180º - 70º - 46º = 64º (hoekensom driehoek 180º)De hoeken D en E zijn de gelijke basishoeken van de gelijkbenige driehoek BED.
∠B2 = ∠B1 = 64º (overstaande hoeken)
Omdat hoek ∠B2 = 64º, is er voor de hoeken D en E nog maar 116º over.
∠E = ∠D = 116º / 2 = 58º
8.
Tip:
Driehoek ACE is gelijkbenig. Dus ∠A2 = ∠C1 (basishoeken zijn gelijk)
a. ∠C2 = 180º - 90º - 77º = 13º (hoekensom driehoek 180º)Driehoek ACE is gelijkbenig. Dus ∠A2 = ∠C1 (basishoeken zijn gelijk)
b. ∠E2 = 180º - 22º - 22º = 136º (hoekensom driehoek 180º)
∠E1 = 180º - 136º = 44º (samen een gestrekte hoek)
c. ∠A1 = 180º - ∠D - ∠E1 = 180º - 90º - 44º = 46º
9.
Antwoord: draaisymmetrie
10.
a. Succes!
b. Ja
c. Ja
d. Zie afbeelding
e. *

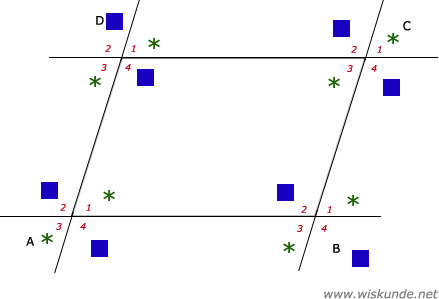
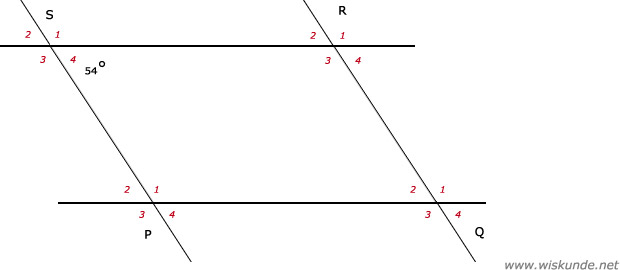
11.
∠S1 = 180º - 54º = 126º
∠P1 = ∠S1 (schuifsymmetrie)
Dus: ∠P = 126º
∠S2 = ∠S4 (overstaande hoeken)
∠Q2 = ∠S2 (schuifsymmetrie)
Dus: ∠Q = 54º
∠P1 = ∠P3 = 126º (overstaande hoeken)
∠R3 = ∠P3 = 126º
Dus: ∠R = 126º
12.
b. ∠B = 180º - 38º - 32º = 110º
c. ∠D1 = 38º (schuifsymmetrie met ∠C)
∠D2 = 180º - 38º = 142º (samen een gestrekte hoek)
d. ∠E1 = 180º - 32º - 38º = 110º
∠E2 = 180º - 110º = 70º (samen een gestrekte hoek)
13.
∠B = 180º - 60º - 75º = 45º (hoekensom driehoek 180º)
∠D1 = ∠A = 60º (schuifsymmetrie)
∠D2 = 180º - 60º = 120º (samen een gestrekte hoek)
∠E1 = ∠B = 45º (schuifsymmetrie)
∠E2 = 180º - 45º = 135º (samen een gestrekte hoek)
14.
∠P = 180º - 71º - 75º = 34º
∠S2 = 180º - 71º = 109º
∠T2 = 180º - 75º = 105º
∠Q = 180º - 75º - 34º = 71º
15.
∠C1 = 180º - 35º - 50º = 95º
∠C2 = ∠A1 = 35º (draaisymmetrie)
∠D = 180º - 35º - 35º = 110º
16.
a. ∠S1 = 180º - 130º = 50º
∠S2 = 130º
∠S3 = ∠S1 = 50º (overstaande hoeken)
∠S4 = ∠S2 = 130º (overstaande hoeken)
b.∠L1 = 180º - 15º - 130º = 35º
∠N1 = 180º - 25º - 50º = 105º
∠L2 = ∠N1 = 105º (draaisymmetrie)
c. ∠N2 = ∠L1 = 35º (draaisymmetrie)
∠M2 = ∠K1 = 15º
17.
b. ∠P1 = 40º
∠P2 = 140º
c. ∠D1 = 70º
∠B1 = 40º
d. ∠S1 = 100º
e. Omdat ∠C1 = ∠D2
18.
b. ∠B1 = 180º - 90º - 29º = 61º
∠B3 = 60º (gelijkzijdige driehoek)
∠B2 = 180º - 61º - 60º = 59º
c. Op basis van symmetrie:
∠C1 = ∠B3 = 60º
∠C2 = ∠B2 = 59º
∠C3 = ∠B1 = 61º
d. ∠F2 = 60º
∠F1 = 180º - 90º - 59º = 31º
∠F3 = ∠F1 = 31º
19.
∠E2 = 180º - 60º = 120º
∠B2 = 90º - 50º = 40º
∠F1 = 180º - ∠B2 - ∠E2 = 180º - 40º - 120º = 20º
∠C2 = 180º - 90º - 25º = 65º
∠C1 = 90º - 65º = 25º
20.
∠C1 = 180º - 90º - 55º = 35º
∠C2 = 60º - 35º = 25º
∠C2 = ∠F1 = 25º (schuifsymmetrie)
∠E3 = 180º - 30º - 25º = 125º
∠G2 = 155º
∠S1 = 180º - 54º = 126º
∠P1 = ∠S1 (schuifsymmetrie)
Dus: ∠P = 126º
∠S2 = ∠S4 (overstaande hoeken)
∠Q2 = ∠S2 (schuifsymmetrie)
Dus: ∠Q = 54º
∠P1 = ∠P3 = 126º (overstaande hoeken)
∠R3 = ∠P3 = 126º
Dus: ∠R = 126º

12.
Tip:
∠D1 = ∠C vanwege schuifsymmetrie
a. Dat zie je door de pijltjes dat ze evenwijdig zijn.∠D1 = ∠C vanwege schuifsymmetrie
b. ∠B = 180º - 38º - 32º = 110º
c. ∠D1 = 38º (schuifsymmetrie met ∠C)
∠D2 = 180º - 38º = 142º (samen een gestrekte hoek)
d. ∠E1 = 180º - 32º - 38º = 110º
∠E2 = 180º - 110º = 70º (samen een gestrekte hoek)
13.
∠B = 180º - 60º - 75º = 45º (hoekensom driehoek 180º)
∠D1 = ∠A = 60º (schuifsymmetrie)
∠D2 = 180º - 60º = 120º (samen een gestrekte hoek)
∠E1 = ∠B = 45º (schuifsymmetrie)
∠E2 = 180º - 45º = 135º (samen een gestrekte hoek)
14.
Tip:
Bekijk eerst met schuifsymmetrie welke hoeken gelijk zijn. Bijvoorbeeld: ∠T1 = ∠R
∠T1 = ∠R = 75ºBekijk eerst met schuifsymmetrie welke hoeken gelijk zijn. Bijvoorbeeld: ∠T1 = ∠R
∠P = 180º - 71º - 75º = 34º
∠S2 = 180º - 71º = 109º
∠T2 = 180º - 75º = 105º
∠Q = 180º - 75º - 34º = 71º
15.
Tip:
De deellijn of bissectrice van een hoek deelt een hoek middendoor. Ofwel in 2 gelijke hoeken.
Zoek op internet eens wat F-hoeken en Z-hoeken zijn. Erg handig.
∠A1 = ∠A2 = 35º (deellijn)De deellijn of bissectrice van een hoek deelt een hoek middendoor. Ofwel in 2 gelijke hoeken.
Zoek op internet eens wat F-hoeken en Z-hoeken zijn. Erg handig.
∠C1 = 180º - 35º - 50º = 95º
∠C2 = ∠A1 = 35º (draaisymmetrie)
∠D = 180º - 35º - 35º = 110º
16.
a. ∠S1 = 180º - 130º = 50º
∠S2 = 130º
∠S3 = ∠S1 = 50º (overstaande hoeken)
∠S4 = ∠S2 = 130º (overstaande hoeken)
b.∠L1 = 180º - 15º - 130º = 35º
∠N1 = 180º - 25º - 50º = 105º
∠L2 = ∠N1 = 105º (draaisymmetrie)
c. ∠N2 = ∠L1 = 35º (draaisymmetrie)
∠M2 = ∠K1 = 15º
17.
Tip:
Verleng de zijden bij de hoekpunten en begin met de schuifsymmetrie.
a. ∠D12 = 110ºVerleng de zijden bij de hoekpunten en begin met de schuifsymmetrie.
b. ∠P1 = 40º
∠P2 = 140º
c. ∠D1 = 70º
∠B1 = 40º
d. ∠S1 = 100º
e. Omdat ∠C1 = ∠D2
18.
Tip:
Door punt F gaat een symmetrieas loodrecht naar beneden.
a. ∠A = ∠D = 29ºDoor punt F gaat een symmetrieas loodrecht naar beneden.
b. ∠B1 = 180º - 90º - 29º = 61º
∠B3 = 60º (gelijkzijdige driehoek)
∠B2 = 180º - 61º - 60º = 59º
c. Op basis van symmetrie:
∠C1 = ∠B3 = 60º
∠C2 = ∠B2 = 59º
∠C3 = ∠B1 = 61º
d. ∠F2 = 60º
∠F1 = 180º - 90º - 59º = 31º
∠F3 = ∠F1 = 31º
19.
Tip:
Er staan geen pijltjes in de tekening voor evenwijdigheid. Dus BE en CF zijn niet evenwijdig.
∠E1 = 180º - 90º - 30º = 60ºEr staan geen pijltjes in de tekening voor evenwijdigheid. Dus BE en CF zijn niet evenwijdig.
∠E2 = 180º - 60º = 120º
∠B2 = 90º - 50º = 40º
∠F1 = 180º - ∠B2 - ∠E2 = 180º - 40º - 120º = 20º
∠C2 = 180º - 90º - 25º = 65º
∠C1 = 90º - 65º = 25º
20.
Tip:
Er zijn pijlen gegeven dus er is sprake van evenwijdigheid. Je kunt dan gebruik maken van schuifsymmetrie.
∠C12 = 180º - 90º - 30º = 60ºEr zijn pijlen gegeven dus er is sprake van evenwijdigheid. Je kunt dan gebruik maken van schuifsymmetrie.
∠C1 = 180º - 90º - 55º = 35º
∠C2 = 60º - 35º = 25º
∠C2 = ∠F1 = 25º (schuifsymmetrie)
∠E3 = 180º - 30º - 25º = 125º
∠G2 = 155º
21.
Helemaal rond is 360º
1 segment is: 360º / 12 = 30º
2 segmenten is: 2 x 30º = 60º
22.
Helemaal rond is 360º
1 segment is: 360º / 24 = 15º
14 segmenten is: 14 x 15º = 210º
Voor de kleinste hoek: 360º - 210º = 150º
23.
Zet de grote wijzer op de 12 en de kleine wijzer tussen de 4 en de 5.
24.
*
Helemaal rond is 360º
1 segment is: 360º / 12 = 30º
2 segmenten is: 2 x 30º = 60º
22.
Helemaal rond is 360º
1 segment is: 360º / 24 = 15º
14 segmenten is: 14 x 15º = 210º
Voor de kleinste hoek: 360º - 210º = 150º
23.
Zet de grote wijzer op de 12 en de kleine wijzer tussen de 4 en de 5.
24.
*
Andere paragrafen:
2.1. Hoeken berekenen in vlakke figuren (1 t/m 24)
2.2. Hoeken berekenen met goniometrie (25 t/m 31)
2.3. Zijden berekenen (32 t/m 46)
2.4. Berekenen van hoeken en afstanden (47 t/m 52)
2.5. Berekeningen in de ruimte (53 t/m 63)
2.6. Coordinaten in de ruimte (64 t/m 78)
2.7. Gemengde opgaven (79 t/m 92)
2.1. Hoeken berekenen in vlakke figuren (1 t/m 24)
2.2. Hoeken berekenen met goniometrie (25 t/m 31)
2.3. Zijden berekenen (32 t/m 46)
2.4. Berekenen van hoeken en afstanden (47 t/m 52)
2.5. Berekeningen in de ruimte (53 t/m 63)
2.6. Coordinaten in de ruimte (64 t/m 78)
2.7. Gemengde opgaven (79 t/m 92)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


