TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 2.3 Zijden berekenen VMBO 4 KGT
Boek: Getal & Ruimte - Hoeken en afstanden VMBO 4 (deel 1) opgaven 32 t/m 46, 2011In een rechthoekige driehoek kunnen zijden en hoeken gegeven zijn.
Wanneer 1 zijde en 1 hoek bekend is, kun je de andere zijden berekenen.
Maak dan gebruik van SOS CAS TOA.
De derde zijde bereken je dan met Pythagoras.
Wanneer 1 zijde en 1 hoek bekend is, kun je de andere zijden berekenen.
Maak dan gebruik van SOS CAS TOA.
De derde zijde bereken je dan met Pythagoras.
32.
33.
sin(56º) = DF / 42
DF = 42 x sin(56º)
DF = 34,82 meter
DF = 3482 cm
34.
tan(21º) = AC / 35
AC = 35 x tan(21º)
AC ≈ 13,44 mm
Dus: AC ≈ 13,4 mm
35.
cos(52º) = 24 / PR
24 = cos(52º) x PR
PR = 24 / cos(52º)
PR ≈ 38,98 ≈ 39 cm
36.
sin(∠K) = O/S = LM/KM
sin(20º) = 4,25 / KM
KM = 4,25 / sin(20º)
KM ≈ 12,43 m
37.
sin(∠A) = O/S = BC/AC
sin(25º) = 78 / AC
78 = AC x sin(25º)
AC = 78 / sin(25º)
AC ≈ 184,56 m
AC ≈ 185 m
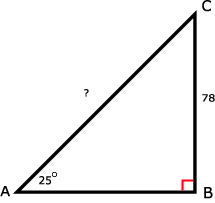
38.
sin(∠A) = O/S = BC/AC
sin(43º) = BC / 180
BC = sin(43º) x 180
BC ≈ 122,76 m
Hoogte vlieger is dus: 122,76 + 1 = 123,76 m
Afgerond: 124 m
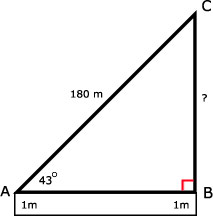
39.
40.
b. Zie boven: 37,95º
c. sin(∠A) = O/S = BC/AC
sin(37,95º) = 352 / AC
AC = 352 / sin(37,95º)
AC ≈ 572,38 m
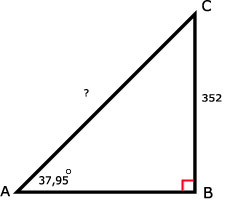
41.
sin(5,71º) = 2,4 / BC
BC = 2,4 / sin(5,71º)
BC ≈ 24,12 m
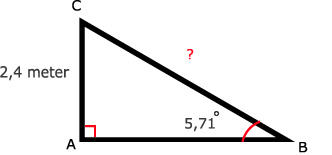
Tip:
sin∠B = O / S = 12 / BC. Met kruislings vermenigvuldigen bereken je BC.
Gebruik de sinus.sin∠B = O / S = 12 / BC. Met kruislings vermenigvuldigen bereken je BC.
33.
Tip:
Kruislings vermenigvuldigen: 2 = 10/5 <=> 2/1 = 10/5 <=> 2 x 5 = 10 x 1
sin(∠E) = O/S = DF/DEKruislings vermenigvuldigen: 2 = 10/5 <=> 2/1 = 10/5 <=> 2 x 5 = 10 x 1
sin(56º) = DF / 42
DF = 42 x sin(56º)
DF = 34,82 meter
DF = 3482 cm
34.
Tip:
Draai de rechthoekige driehoek altijd zo dat de rechte hoek (90º) "op de grond" ligt. Dan zie je het beter.
tan(∠B) = O/A = AC/ABDraai de rechthoekige driehoek altijd zo dat de rechte hoek (90º) "op de grond" ligt. Dan zie je het beter.
tan(21º) = AC / 35
AC = 35 x tan(21º)
AC ≈ 13,44 mm
Dus: AC ≈ 13,4 mm
35.
Tip:
Gegeven een hoek en een zijde. Je kunt dus een andere zijde berekenen.
Begin met de hoek die je weet. Dus ...(52º) = ...
cos(∠R) = A/S = QR/PRGegeven een hoek en een zijde. Je kunt dus een andere zijde berekenen.
Begin met de hoek die je weet. Dus ...(52º) = ...
cos(52º) = 24 / PR
24 = cos(52º) x PR
PR = 24 / cos(52º)
PR ≈ 38,98 ≈ 39 cm
36.
sin(∠K) = O/S = LM/KM
sin(20º) = 4,25 / KM
KM = 4,25 / sin(20º)
KM ≈ 12,43 m
37.
sin(∠A) = O/S = BC/AC
sin(25º) = 78 / AC
78 = AC x sin(25º)
AC = 78 / sin(25º)
AC ≈ 184,56 m
AC ≈ 185 m

38.
sin(∠A) = O/S = BC/AC
sin(43º) = BC / 180
BC = sin(43º) x 180
BC ≈ 122,76 m
Hoogte vlieger is dus: 122,76 + 1 = 123,76 m
Afgerond: 124 m

39.
Tip:
Een helling geven we weer met een hellingspercentage.
Het juiste bord is bordje 3 met 15%.Een helling geven we weer met een hellingspercentage.
40.
Tip:
tan(∠A) = hellingspercentage : 100%
tan(∠A) = 78% : 100% = 0,78
∠A = tan-1(0,78)
∠A ≈ 37,95º
a. Zie afbeeldingtan(∠A) = hellingspercentage : 100%
tan(∠A) = 78% : 100% = 0,78
∠A = tan-1(0,78)
∠A ≈ 37,95º
b. Zie boven: 37,95º
c. sin(∠A) = O/S = BC/AC
sin(37,95º) = 352 / AC
AC = 352 / sin(37,95º)
AC ≈ 572,38 m

41.
Tip:
tan(∠B) = hellingspercentage : 100%
tan(∠B) = 10% : 100% = 0,10
∠B = tan-1(0,10)
∠B ≈ 5,71º
sin(∠B) = O/S = AC/BCtan(∠B) = hellingspercentage : 100%
tan(∠B) = 10% : 100% = 0,10
∠B = tan-1(0,10)
∠B ≈ 5,71º
sin(5,71º) = 2,4 / BC
BC = 2,4 / sin(5,71º)
BC ≈ 24,12 m

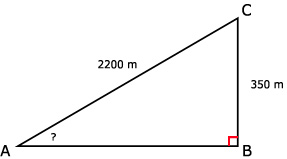
42.
AB2 + 3502 = 22002
AB2 = 4 717 500
AB ≈ 2171,98 m
hellings % = (350/2171,98) x 100% = 16,11%
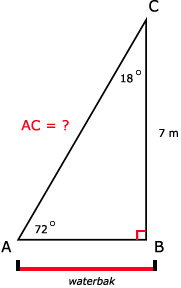
43.
cos(18º) = 7 / AC
AC = 7 / cos(18º)
AC ≈ 7,36 m
l = 7,36 / 7 = 1,05 m
Dus: 105 cm
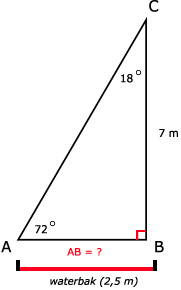
44.
tan(72º) = 7 / AB
AB = 7 / tan(72º)
AB ≈ 2,27 m
Dus C ligt boven de waterbak.
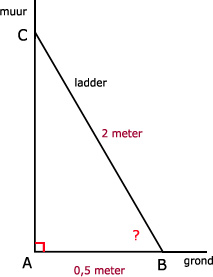
45.
∠B = cos-1(0,25)
∠B ≈ 75,5º
46.
tan(18º) = BC/7
BC = 7 x tan(18º) ≈ 2,27 m
oppervlakte driehoek ABC = 1/2 x zijde x bijbehorende hoogte
opp(ABC) = 1/2 x 7 x 2,27
opp(ABC) = 7,945 m2
Inhoud prisma = 7,945 x 14 = 111,23 m3
Dus Rob heeft gelijk.
Tip:
Bereken eerst AB met de Stelling van Pythagoras en gebruik dan de Tan.
AB2 + BC2 = AC2Bereken eerst AB met de Stelling van Pythagoras en gebruik dan de Tan.
AB2 + 3502 = 22002
AB2 = 4 717 500
AB ≈ 2171,98 m
hellings % = (350/2171,98) x 100% = 16,11%

43.
Tip:
Maak een schets met ∠A = 180º - 108º = 72º. Hoek C is 90º - 72º = 18º. BC = 7 is hoogte gevel.
AC is de schuine gevel.
cos(∠C) = A/S = BC/ACMaak een schets met ∠A = 180º - 108º = 72º. Hoek C is 90º - 72º = 18º. BC = 7 is hoogte gevel.
AC is de schuine gevel.
cos(18º) = 7 / AC
AC = 7 / cos(18º)
AC ≈ 7,36 m
l = 7,36 / 7 = 1,05 m
Dus: 105 cm

44.
Tip:
Vraag: hoe lang is AB? Als AB kleiner is dan 2,5 m dan ligt C boven de waterbak. Is AB groter dan 2,5 m dan ligt C buiten/rechts van de waterbak.
tan(∠A) = O/A = BC/ABVraag: hoe lang is AB? Als AB kleiner is dan 2,5 m dan ligt C boven de waterbak. Is AB groter dan 2,5 m dan ligt C buiten/rechts van de waterbak.
tan(72º) = 7 / AB
AB = 7 / tan(72º)
AB ≈ 2,27 m
Dus C ligt boven de waterbak.

45.
Tip:
Stel ladder = 2 m. Dan is de afstand AB = 0,5 m.
Of stel ladder = 4 m. Dan is de afstand AB = 1 m.
cos(∠B) = A/S = AB/BC = 0,5/2 = 0,25Stel ladder = 2 m. Dan is de afstand AB = 0,5 m.
Of stel ladder = 4 m. Dan is de afstand AB = 1 m.
∠B = cos-1(0,25)
∠B ≈ 75,5º

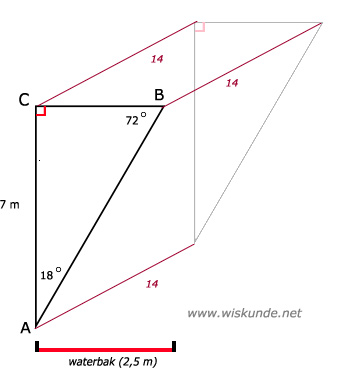
46.
Tip:
Inhoud prisma = oppervlakte driehoek ABC x hoogte
hoogte prisma h = 14
Bereken eerst BC
tan(∠A) = O/A = BC/AC = BC/7Inhoud prisma = oppervlakte driehoek ABC x hoogte
hoogte prisma h = 14
Bereken eerst BC
tan(18º) = BC/7
BC = 7 x tan(18º) ≈ 2,27 m
oppervlakte driehoek ABC = 1/2 x zijde x bijbehorende hoogte
opp(ABC) = 1/2 x 7 x 2,27
opp(ABC) = 7,945 m2
Inhoud prisma = 7,945 x 14 = 111,23 m3
Dus Rob heeft gelijk.

Andere paragrafen:
2.1. Hoeken berekenen in vlakke figuren (1 t/m 24)
2.2. Hoeken berekenen met goniometrie (25 t/m 31)
2.3. Zijden berekenen (32 t/m 46)
2.4. Berekenen van hoeken en afstanden (47 t/m 52)
2.5. Berekeningen in de ruimte (53 t/m 63)
2.6. Coordinaten in de ruimte (64 t/m 78)
2.7. Gemengde opgaven (79 t/m 92)
2.1. Hoeken berekenen in vlakke figuren (1 t/m 24)
2.2. Hoeken berekenen met goniometrie (25 t/m 31)
2.3. Zijden berekenen (32 t/m 46)
2.4. Berekenen van hoeken en afstanden (47 t/m 52)
2.5. Berekeningen in de ruimte (53 t/m 63)
2.6. Coordinaten in de ruimte (64 t/m 78)
2.7. Gemengde opgaven (79 t/m 92)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


