TIP: Wil je ook toegang tot meer dan 17.300 video-uitwerkingen? Meld je dan snel aan! Klik hier...
Antwoorden 2.5 Berekeningen in de ruimte VMBO 4 KGT
Boek: Getal & Ruimte - Hoeken en afstanden VMBO 4 (deel 1) opgaven 53 t/m 63, 2011In een balk kunnen we de lengte van een lichaamsdiagonaal berekenen met de verlengde Stelling van Pythagoras.
Je gebruikt dan drie korte zijden i.p.v. twee. Hierbij maak je gebruik van het bekende schema.
Om de verlengde Stelling van Pythagoras te gebruiken, maak een schets van het juiste diagonaalvlak en teken daarin de juiste rechthoekige driehoek.
Je gebruikt dan drie korte zijden i.p.v. twee. Hierbij maak je gebruik van het bekende schema.
Om de verlengde Stelling van Pythagoras te gebruiken, maak een schets van het juiste diagonaalvlak en teken daarin de juiste rechthoekige driehoek.
53.
a. BH ligt in diagonaalvlak DBFH.
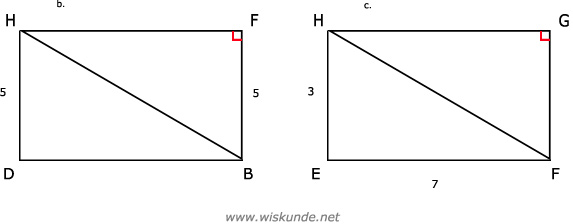
b. Zie afbeelding b.
c. Zie afbeelding c.
FH = √58 ≈ 7,6
d. Zie afbeelding b.
BH = √82,76 ≈ 9,10
54.
b. EC ligt in diagonaalvlak EACG
c. *
d. Zie afbeelding
e.
EC = √83 ≈ 9,11
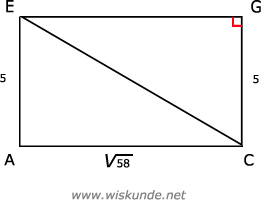
55.
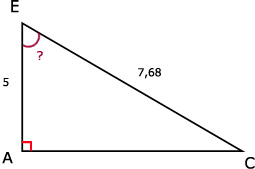
CE = √59 ≈ 7,68
b. Zie afbeelding
cos(∠E) = A/S = AE/EC
cos(∠E) = 5 / 7,68
∠E = cos-1(5/7,68)
∠E ≈ 49,38º
56.
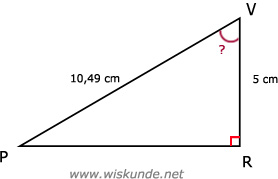
PV = √110 ≈ 10,49 cm
PV = 105 mm
b. Zie afbeelding
cos(∠V) = A/S = VR/PV
cos(∠V) = 5 / 10,49
∠V = cos-1(5/10,49)
∠V ≈ 61,53º
57.
PQ = √51,25 ≈ 7,2
BS = √68 ≈ 8,2
RS = √41 ≈ 6,4
58.
rood2 = 3875
rood = √3875 ≈ 62,25 cm
59.
b.
AC = √113 ≈ 10,63
AS = 1/2 x AC = 1/2 x 10,63 = 5,32
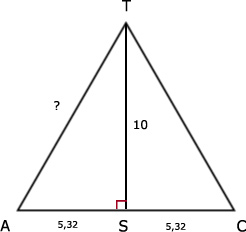
c.
AT = √128,3 ≈ 11,33
60.
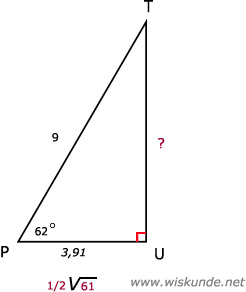
PR = √61 ≈ 7,81
PU = 1/2 x PR = 1/2 x 7,81 = 3,91
sin(∠TPU) = O/S = TU/PT
sin(62º) = TU / 9
TU = sin(62º) x 9
TU ≈ 7,95 cm
61.
b. tan(∠VEA) = O/A = AV/AE
tan(72º) = AV / 40
AV = tan(72º) x 40
AV ≈ 123,11 m
c. tan(∠AEP) = O/A = AP/AE
tan(78º) = AP / 40
AP = tan(78º) x 40
AP ≈ 188,19 m

62.
b. Zie afbeelding
c.
VP = √50 571,55 ≈ 224,88

a. BH ligt in diagonaalvlak DBFH.
b. Zie afbeelding b.
c. Zie afbeelding c.
| -> kwadraat | ||
| EF = 7 | | | 49 |
| EH = 3 | | | 9 |
| ----------- + | ||
| FH = ? | | | 58 |
| <- wortel |
FH = √58 ≈ 7,6
d. Zie afbeelding b.
| -> kwadraat | ||
| FH = 7,6 | | | 57,76 |
| BF = 5 | | | 25 |
| ----------- + | ||
| BH = ? | | | 82,76 |
| <- wortel |
BH = √82,76 ≈ 9,10

54.
Tip:
AC en FH zijn even lang. Dus AC = FH = √58
a. *AC en FH zijn even lang. Dus AC = FH = √58
b. EC ligt in diagonaalvlak EACG
c. *
d. Zie afbeelding
e.
| -> kwadraat | ||
| AE = 5 | | | 25 |
| AC = √58 | | | 58 |
| ----------- + | ||
| EC = ? | | | 83 |
| <- wortel |
EC = √83 ≈ 9,11

55.
Tip:
Maak altijd eerst een goede schets van de juiste rechthoekige driehoek. Teken in je schets de afmetingen die je kent.
a. Maak altijd eerst een goede schets van de juiste rechthoekige driehoek. Teken in je schets de afmetingen die je kent.
| -> kwadraat | ||
| BC = 3 | | | 9 |
| AB = 5 | | | 25 |
| AE = 5 | | | 25 |
| ----------- + | ||
| CE = ? | | | 59 |
| <- wortel |
CE = √59 ≈ 7,68
b. Zie afbeelding
cos(∠E) = A/S = AE/EC
cos(∠E) = 5 / 7,68
∠E = cos-1(5/7,68)
∠E ≈ 49,38º

56.
Tip:
PV = √110 ≈ 10,49. Je kunt dus in het verdere verloop rekenen met 10,49 maar eigenlijk is het beter om verder te rekenen met √110. Dat is namelijk nauwkeuriger.
a. PV = √110 ≈ 10,49. Je kunt dus in het verdere verloop rekenen met 10,49 maar eigenlijk is het beter om verder te rekenen met √110. Dat is namelijk nauwkeuriger.
| -> kwadraat | ||
| PQ = 6 | | | 36 |
| QR = 7 | | | 49 |
| RV = 5 | | | 25 |
| ----------- + | ||
| PV = ? | | | 110 |
| <- wortel |
PV = √110 ≈ 10,49 cm
PV = 105 mm
b. Zie afbeelding
cos(∠V) = A/S = VR/PV
cos(∠V) = 5 / 10,49
∠V = cos-1(5/10,49)
∠V ≈ 61,53º

57.
Tip:
Gebruik steeds de verlengde Stelling van Pythagoras.
Gebruik steeds de verlengde Stelling van Pythagoras.
| -> kwadraat | ||
| PB = 3 | | | 9 |
| BC = 6 | | | 36 |
| CQ = 2,5 | | | 6,25 |
| ----------- + | ||
| PQ = ? | | | 51,25 |
| <- wortel |
PQ = √51,25 ≈ 7,2
| -> kwadraat | ||
| BC = 6 | | | 36 |
| CG = 4 | | | 16 |
| GS = 4 | | | 16 |
| ----------- + | ||
| BS = ? | | | 68 |
| <- wortel |
BS = √68 ≈ 8,2
| -> kwadraat | ||
| RE = 2 | | | 4 |
| EH = 6 | | | 36 |
| HS = 1 | | | 1 |
| ----------- + | ||
| RS = ? | | | 41 |
| <- wortel |
RS = √41 ≈ 6,4
58.
Tip:
De rode draad is een lichaamsdiagonaal in een balk. Gebruik de verlengde Stelling van Pythagoras.
rood2 = 452 + 352 + 252De rode draad is een lichaamsdiagonaal in een balk. Gebruik de verlengde Stelling van Pythagoras.
rood2 = 3875
rood = √3875 ≈ 62,25 cm
59.
Tip:
AS is de helft van AC.
a. Zie afbeeldingAS is de helft van AC.
b.
| -> kwadraat | ||
| AB = 8 | | | 64 |
| BC = 7 | | | 49 |
| ----------- + | ||
| AC = ? | | | 113 |
| <- wortel |
AC = √113 ≈ 10,63
AS = 1/2 x AC = 1/2 x 10,63 = 5,32
c.
| -> kwadraat | ||
| AS = 5,32 | | | 28,3 |
| TS = 10 | | | 100 |
| ----------- + | ||
| AT = ? | | | 128,3 |
| <- wortel |
AT = √128,3 ≈ 11,33

60.
Tip:
Bereken eest PR met de Stelling van Pythagoras en neem dan de helft voor PU.
Aangezien PR = √61 dan is PU de helft dus ½√61. Dat is nauwkeuriger.
Bereken eerst PR:Bereken eest PR met de Stelling van Pythagoras en neem dan de helft voor PU.
Aangezien PR = √61 dan is PU de helft dus ½√61. Dat is nauwkeuriger.
| -> kwadraat | ||
| PQ = 5 | | | 25 |
| QR = 6 | | | 36 |
| ----------- + | ||
| PR = ? | | | 61 |
| <- wortel |
PR = √61 ≈ 7,81
PU = 1/2 x PR = 1/2 x 7,81 = 3,91
sin(∠TPU) = O/S = TU/PT
sin(62º) = TU / 9
TU = sin(62º) x 9
TU ≈ 7,95 cm

61.
Tip:
AV is de afstand van vader tot de toren
AP is de afstand van parkeerplaats tot de toren
a. Zie afbeeldingAV is de afstand van vader tot de toren
AP is de afstand van parkeerplaats tot de toren
b. tan(∠VEA) = O/A = AV/AE
tan(72º) = AV / 40
AV = tan(72º) x 40
AV ≈ 123,11 m
c. tan(∠AEP) = O/A = AP/AE
tan(78º) = AP / 40
AP = tan(78º) x 40
AP ≈ 188,19 m

62.
Tip:
De hoek tussen het Noorden en het Oosten is 90 graden.
a. Het Oosten staat loodrecht op het Zuiden.De hoek tussen het Noorden en het Oosten is 90 graden.
b. Zie afbeelding
c.
| -> kwadraat | ||
| AV = 123,11 | | | 15 156,07 |
| AP = 188,19 | | | 35 415,48 |
| ----------- + | ||
| VP = ? | | | 50 571,55 |
| <- wortel |
VP = √50 571,55 ≈ 224,88

63.
b. Zie afbeelding
c. *
d. cos(∠B) = A/S = BD/AB
cos(68º) = BD / 90
BD = cos(68º) x 90
BD ≈ 33,71 cm
BC = 2 x BD = 2 x 33,71 = 67,43 cm
Dat is dus 0,67 meter.
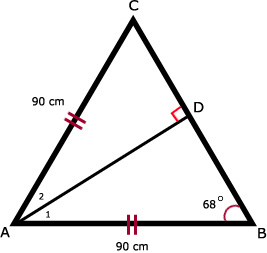
Tip:
Bereken eerst BD. Dan uitzethaak BC = 2 x BD.
a. Omdat gegeven is dat AC = AB = 90 cm.Bereken eerst BD. Dan uitzethaak BC = 2 x BD.
b. Zie afbeelding
c. *
d. cos(∠B) = A/S = BD/AB
cos(68º) = BD / 90
BD = cos(68º) x 90
BD ≈ 33,71 cm
BC = 2 x BD = 2 x 33,71 = 67,43 cm
Dat is dus 0,67 meter.

Andere paragrafen:
2.1. Hoeken berekenen in vlakke figuren (1 t/m 24)
2.2. Hoeken berekenen met goniometrie (25 t/m 31)
2.3. Zijden berekenen (32 t/m 46)
2.4. Berekenen van hoeken en afstanden (47 t/m 52)
2.5. Berekeningen in de ruimte (53 t/m 63)
2.6. Coordinaten in de ruimte (64 t/m 78)
2.7. Gemengde opgaven (79 t/m 92)
2.1. Hoeken berekenen in vlakke figuren (1 t/m 24)
2.2. Hoeken berekenen met goniometrie (25 t/m 31)
2.3. Zijden berekenen (32 t/m 46)
2.4. Berekenen van hoeken en afstanden (47 t/m 52)
2.5. Berekeningen in de ruimte (53 t/m 63)
2.6. Coordinaten in de ruimte (64 t/m 78)
2.7. Gemengde opgaven (79 t/m 92)
Hoe maken wij onze video's?
Word ook lid!
Word ook lid!
Ook van ons:
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)
Brugklas.net
Vmbobasis.nl
Vmbokader.nl
Mavo3.nl
Mavo4.nl
Havo1.nl
Havo2.nl
Havo3.nl
Vwo1.nl
Vwo2.nl
Vwo3.nl
Wiskunde-a.nl (4/5/6)
Wiskunde-b.nl (4/5/6)
Wiskunde-c.nl (4/5/6)
Wiskunde-d.nl (4/5/6)
Wiskundeles.nl
Wiskunde.help
Wiskunde.LIVE (later meer)
Wiskunde examentraining (2026)


