Wiskunde.net

Machten

01-05-2025admin23

Inleiding

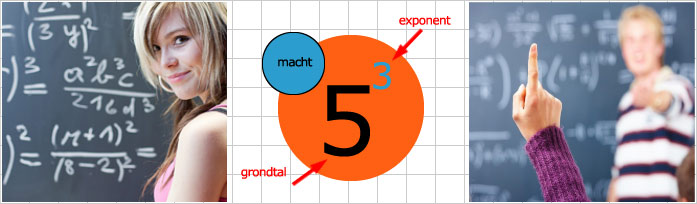
Machtsverheffen is een operatie in de Wiskunde die we schrijven als xⁿ. Een macht heeft een grondtal en een exponent. Wanneer n groter dan 0 is, hebben we te maken met een herhaalde vermenigvuldiging. Een macht ziet er als volgt uit: 5³. We noemen dan 5³ de macht en 5 is het grondtal en 3 is de exponent. We spreken dit uit als '5 tot de macht 3'. Uitkomst hiervan is 5*5*5=125.

Regels van machten:
(1) a^p * a^q = a^p+q
(2) (a^p)^q = a^p*q
(3) (a*b)^p = a^p * b^p
(4) a^p / a^q = a^p-q

We gaan de rekenregels van machten wat nader toelichten:

Rekenregel 1: Product van machten
Een product van machten met hetzelfde grondtal kun je herleiden tot 1 macht door de exponenten bij elkaar op te tellen.
Voorbeeld: 5a⁴ * 3a³ = 5 * 3 * a⁴ * a³ = 5 * 3 * a⁴⁺³ = 15a⁷

Rekenregel 2: Een macht van een macht
Bij een macht van een macht moet je de exponenten met elkaar vermenigvuldigen.
Voorbeeld: (x³)⁴ = x³ * x³ * x³ * x³ = x^3+3+3+3 = x¹²
ofwel, x^3*4

Rekenregel 3: Een macht van een product
Bij een macht van een product neem je elke factor tot die macht.
Voorbeeld: (2x)⁴ = 2⁴ * x⁴ = 16x⁴

Rekenregel 4: Het delen van machten
Bij het delen van machten met hetzelfde grondtal moet je de exponenten aftrekken.
Voorbeeld: a¹¹ / a⁶ = a^11-6 = a⁵

Formule Machten

Voorbeelden Machten

Extra