Wiskunde.netLogo Wiskunde


Inhoud kegel

LET OP: Wil je ook toegang tot meer dan 15.000 video-uitwerkingen voor 36 euro per jaar? Meld je dan snel aan! Klik hier...
Wiskunde01-12-2024admin23
Inhoud kegel

Inleiding

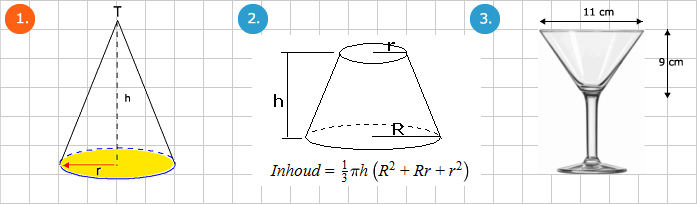
Een kegel is een ruimtelijke figuur. Een kegel bestaat uit een plat vlak en een gekromd vlak. Het platte vlak is de bodem. Deze bodem is een cirkel. Het gekromde vlak is de mantel van de kegel. De lijn uit de top (T) van de kegel loodrecht op de grondcirkel door het middelpunt van de grondcirkel noemen we de hoogte van de kegel.
De hoogte horende bij de inhoud van een kegel noteren we vaak als h (afb. 1). De oppervlakte van de grondcirkel van de kegel is πr2. Net zo als bij een piramide om de inhoud te bepalen vermenigvuldigen we 1/3 met de oppervlakte grondvlak maal de hoogte van de ruimtefiguur.

Een andere naam voor kegel is conus. Een kegel kun je op meerdere manieren doorsnijden. De kegeldoorsneden kunnen dan zijn: een cirkel, een ellips, een parabool en een hyperbool. Een afgeknotte kegel (afb. 2) is een ruimtelijke figuur (kegel) waar een stuk van afgesneden is. Denk aan een emmer of bloempot.
De inhoud van een afgeknotte kegel is: ⅓ π h ( R2 + Rr + r2)

Formule Inhoud kegel

inhoud kegel = 1/3 x oppervlakte grondvlak x hoogte = 1/3 x π r2 x h

Voorbeelden Inhoud kegel

Voorbeeld 1
Bereken de inhoud in liters van een kegel met hoogte 51 cm en met diameter van grondcirkel 14 cm.
Rond af op 2 decimalen.

Uitwerking:
Hieruit volgt dus dat de straal van de cirkel: r = 7
Gebruik formule: inhoud kegel = 1/3 x oppervlakte grondvlak x hoogte
Invullen levert: => inhoud kegel = 1/3 x π x r2 x h = 1/3 x π x 72 x 51 = 1/3 x π x 49 x 51 = 2616,95 cm3
1 liter = 1 dm3 = 1000 cm3
Dus 2616,95 cm3 = 2,62 liter

Voorbeeld 2 (afb. 3)
Gegeven een wijnglas met een diameter van 11 cm.
Bereken in cm3 hoeveel wijn er in het glas kan. Rond af op 1 decimaal.

Uitwerking:
Het betreft hier dus een omgekeerde kegel. We weten dat de straal van de cirkel is: r = 5,5
Gebruik formule: inhoud kegel = 1/3 x oppervlakte grondvlak x hoogte
Invullen levert: => inhoud kegel = 1/3 x π x r2 x h = 1/3 x π x 5,52 x 9 = 1/3 x π x 30,25 x 9 = 285,09 cm3
Afgerond op 1 decimaal is de inhoud van het wijnglas: 285,1 cm3

Extra

De oppervlakte van een kegel is de som van de oppervlakten van de grondcirkel en de kegelmantel.
Dit wordt dus: Opp(kegel) = Opp(grondcirkel) + Opp(kegelmantel) = πr2 + πrR
Met r de straal van de grondcirkel en R de straal van de cirkelsector van de uitslag van de mantel.

Gerelateerd

Oppervlakte kegel De oppervlakte van een kegel bestaat uit 2 onderdelen. De kegelmantel en de gron...
Inhoud piramide Een piramide is een meetkundig figuur in de Wiskunde die bestaat uit een grondvl...
Inhoud cilinder Een cilinder is een bekende meetkundige figuur en bestaat uit drie onderdelen. E...
Inhoud prisma Een prisma is een meetkundig figuur dat bestaat uit allemaal rechthoeken, behalv...
Inhoud bol Een bol is een ruimtefiguur. Vaak noemen we dit ook wel een driedimensionaal lic...

Video

Wiskunde.net © 2013 - 2024